广西壮族自治区钦州市浦北县2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-17 类型:期末考试
一、单选题
-
1. 下列图形中,不一定是轴对称图形的是( )A、圆 B、等边三角形 C、正方形 D、梯形2. 下列式子中,是分式的是( )A、 B、 C、 D、3. 将0.0000164用科学记数法表示为( )A、 B、 C、 D、4. 已知三角形的两边长分别为 和 ,则它的第三边长可能是( )A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 下列所叙述的三角形一定全等的是( )A、边长相等的两个正三角形 B、腰相等的两个等腰三角形 C、含有30°角的两个直角三角形 D、两边和其中一边的对角分别相等的两个三角形7. 一个多边形的内角和是外角和的2倍,这个多边形的边数为( )A、5 B、6 C、7 D、88. 如果 ,那么 的值为( )A、 B、 C、 D、9. 如图,从边长为 的大正方形纸片中挖去一个边长为 的小正方形纸片后,将其裁成四个相同的等腰梯形(甲),然后拼成一个平行四边形(乙).那么通过计算两个图形阴影部分的面积,可以验证成立的公式是( )
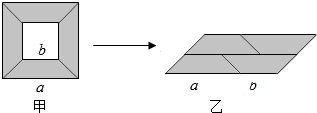 A、 B、 C、 D、10. 已知等腰 的底边 ,且 ,则它的周长为( )A、12 B、16 C、32 D、16或3211. 如图,△ABC中,AB=4,BC=6,BD是△ABC的角平分线,DE⊥AB于点E,AF⊥BC于点F,若DE=2,则AF的长为( )
A、 B、 C、 D、10. 已知等腰 的底边 ,且 ,则它的周长为( )A、12 B、16 C、32 D、16或3211. 如图,△ABC中,AB=4,BC=6,BD是△ABC的角平分线,DE⊥AB于点E,AF⊥BC于点F,若DE=2,则AF的长为( ) A、3 B、 C、 D、12. 如图,过边长为3的等边 的边 上一点 ,作 于 , 为 延长线上一点,当 时,连接 交边 于点 ,则 的长为( )
A、3 B、 C、 D、12. 如图,过边长为3的等边 的边 上一点 ,作 于 , 为 延长线上一点,当 时,连接 交边 于点 ,则 的长为( )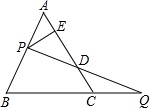 A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
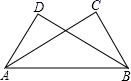
13. 计算: .14. 在平面直角坐标系中,点 关于x轴对称的点的坐标是.15. 要使分式 有意义,则 的取值范围是 .16. 如图,在△ABC和△BAD中,已知∠C=∠D=90°,再添加一个条件,就可以用“HL”判定Rt△ABC≌Rt△BAD , 你添加的条件是 .
 17. 如图,在 中, 是 的垂直平分线,与 交于点 , , ,则 的长为 .
17. 如图,在 中, 是 的垂直平分线,与 交于点 , , ,则 的长为 . 18. 在 中, , , 为边 上的点,联结 (如图所示),如果将 沿直线 翻折后,点 恰好落在边 的中点处,那么点 到 的距离是 .
18. 在 中, , , 为边 上的点,联结 (如图所示),如果将 沿直线 翻折后,点 恰好落在边 的中点处,那么点 到 的距离是 .
三、解答题
-
19. 因式分解:(1)、 ;(2)、 .20. 先化简,再求值: ,其中 .21. 尺规作图(保留作图痕迹,不要求写出什么作法):
如图,已知 ,求作:

( 1 ) 的角平分线;
( 2 )边 上的中线.
22. 如图,在 中, 是高, , 是角平分线,它们相交于点 , , ,求 和 的度数. 23. 如图,在 中,点 , 分别是 , 边上的点, , , 与 相交于点 .求证:
23. 如图,在 中,点 , 分别是 , 边上的点, , , 与 相交于点 .求证: (1)、 ;(2)、 是等腰三角形.24. 甲、乙两个服装厂加工同种型号的防护服,甲厂每天加工的数量是乙厂每天加工数量的1.5倍,两厂各加工600套防护服,甲厂比乙厂要少用4天.(1)、求甲、乙两厂每天各加工多少套防护服?(2)、已知甲、乙两厂加工这种防护服每天的费用分别是150元和120元,疫情期间,某医院紧急需要3000套这种防护服,甲厂单独加工一段时间后另有安排,剩下任务只能由乙单独完成.如果总加工费不超过6360元,那么甲厂至少要加工多少天?25. 如图,在 中, ,点 在 边上,且 , 是 上一动点(不与点 重合,且 ),在 上截取 ,连接 .
(1)、 ;(2)、 是等腰三角形.24. 甲、乙两个服装厂加工同种型号的防护服,甲厂每天加工的数量是乙厂每天加工数量的1.5倍,两厂各加工600套防护服,甲厂比乙厂要少用4天.(1)、求甲、乙两厂每天各加工多少套防护服?(2)、已知甲、乙两厂加工这种防护服每天的费用分别是150元和120元,疫情期间,某医院紧急需要3000套这种防护服,甲厂单独加工一段时间后另有安排,剩下任务只能由乙单独完成.如果总加工费不超过6360元,那么甲厂至少要加工多少天?25. 如图,在 中, ,点 在 边上,且 , 是 上一动点(不与点 重合,且 ),在 上截取 ,连接 . (1)、若点 与点 重合时,求证: ;(2)、若点 不与 重合,线段 , 和 有怎样的数量关系?证明你的结论.
(1)、若点 与点 重合时,求证: ;(2)、若点 不与 重合,线段 , 和 有怎样的数量关系?证明你的结论.