广西壮族自治区贵港市港南区2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-17 类型:期末考试
一、单选题
-
1. 下列各式中,是一元一次不等式的是( )A、 B、 C、 D、2. 下列实数中,属于无理数的是( )A、0 B、 C、 D、73. 下列说法正确的是 ( )
A、-81的平方根是±9 B、任何数的平方是非负数,因而任何数的平方根也是非负数 C、任何一个非负数的平方根都不大于这个数 D、2是4的平方根4. ( )A、 B、 C、 D、5. 下列用数轴表示不等式组 的解集正确的是( )A、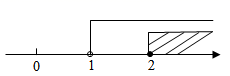 B、
B、 C、
C、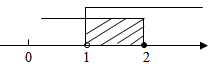 D、
D、 6. 下列命题中,是真命题的是( )A、同位角相等 B、相等的角是对顶角 C、邻补角一定互补 D、有且只有一条直线与已知直线垂直7. 已知 ,下列式子不成立的是( )A、 B、 C、 D、 ,那么8. “新冠肺炎”知识竞赛共20道题,每答对一题得10分,答错或不答都扣5分,小颖得分不低于 90 分.设她答对了 x道题,根据题意可列出的不等式为( )A、10x﹣5(20﹣x)≥90 B、10x﹣5(20﹣x)>90 C、10x﹣(20﹣x)≥90 D、10x﹣(20﹣x)>909. 工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的到刻度分别与点M、N重合,过角尺顶点C作射线OC由此作法便可得△NOC≌△MOC,其依据是( )
6. 下列命题中,是真命题的是( )A、同位角相等 B、相等的角是对顶角 C、邻补角一定互补 D、有且只有一条直线与已知直线垂直7. 已知 ,下列式子不成立的是( )A、 B、 C、 D、 ,那么8. “新冠肺炎”知识竞赛共20道题,每答对一题得10分,答错或不答都扣5分,小颖得分不低于 90 分.设她答对了 x道题,根据题意可列出的不等式为( )A、10x﹣5(20﹣x)≥90 B、10x﹣5(20﹣x)>90 C、10x﹣(20﹣x)≥90 D、10x﹣(20﹣x)>909. 工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的到刻度分别与点M、N重合,过角尺顶点C作射线OC由此作法便可得△NOC≌△MOC,其依据是( )
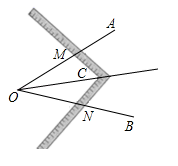 A、SSS B、SAS C、ASA D、AAS10. 如图,△ABC中,∠C=90°,ED垂直平分AB , 若AC=12,EC=5,且△ACE的周长为30,则BE的长为( )
A、SSS B、SAS C、ASA D、AAS10. 如图,△ABC中,∠C=90°,ED垂直平分AB , 若AC=12,EC=5,且△ACE的周长为30,则BE的长为( )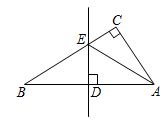 A、5 B、10 C、12 D、1311. 如图,∠MON=90°,点A,B分别在射线OM,ON上运动,BE平分∠NBA,BE的反向延长线与∠BAO的平分线交于点C,则∠C的度数是( )
A、5 B、10 C、12 D、1311. 如图,∠MON=90°,点A,B分别在射线OM,ON上运动,BE平分∠NBA,BE的反向延长线与∠BAO的平分线交于点C,则∠C的度数是( ) A、30° B、45° C、55° D、60°12. 如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法:①△ABE的面积=△BCE的面积;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.其中正确的是( )
A、30° B、45° C、55° D、60°12. 如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法:①△ABE的面积=△BCE的面积;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.其中正确的是( ) A、①②③④ B、①②③ C、②④ D、①③
A、①②③④ B、①②③ C、②④ D、①③二、填空题
-
13. 当x=时,分式 的值为0.14. 一个三角形的三边为2、5、x , 另一个三角形的三边为y、2、6,若这两个三角形全等,则x+y= .15. 不等式组 的解集是 .16. 已知 ,则 .17. 对于整数a,b,c,d,符号 表示运算ad﹣bc,已知1< <3,则bd的值是 .
三、解答题
-
18.(1)、计算: .(2)、先化简,再求值: ,其中 .19. 如图,在 中, .
 (1)、尺规作图:在AC上找一点D,使得 (不写作法,保留作图迹);(2)、连接BD,若 ,请直接写出 的度数.20. 解不等式: ,并把解集表示在数轴上.21. 正数x的两个平方根分别为3﹣a和2a+7.(1)、求a的值;(2)、求44﹣x这个数的立方根.22. 某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售2辆A型车和1辆B型车,销售额为62万元.(1)、求每辆A型车和B型车的售价各多少万元.(2)、甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元. 则有哪几种购车方案?23. 如图,在△ABC中,AB=AC,BD=CF,BE=CD.
(1)、尺规作图:在AC上找一点D,使得 (不写作法,保留作图迹);(2)、连接BD,若 ,请直接写出 的度数.20. 解不等式: ,并把解集表示在数轴上.21. 正数x的两个平方根分别为3﹣a和2a+7.(1)、求a的值;(2)、求44﹣x这个数的立方根.22. 某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售2辆A型车和1辆B型车,销售额为62万元.(1)、求每辆A型车和B型车的售价各多少万元.(2)、甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元. 则有哪几种购车方案?23. 如图,在△ABC中,AB=AC,BD=CF,BE=CD. (1)、求证:△BDE≌△CFD;(2)、若∠A=70°,求∠EDF的度数.24. 已知方程组 ,其中x为非正数,y为负数.(1)、求m的取值范围;(2)、化简:|m﹣3|﹣|m+2|;(3)、不等式2mx+x<2m+1的解集为x>1,求m的整数值.25. 已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)、求证:△BDE≌△CFD;(2)、若∠A=70°,求∠EDF的度数.24. 已知方程组 ,其中x为非正数,y为负数.(1)、求m的取值范围;(2)、化简:|m﹣3|﹣|m+2|;(3)、不等式2mx+x<2m+1的解集为x>1,求m的整数值.25. 已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°. (1)、如图1,若AB∥ON,则
(1)、如图1,若AB∥ON,则①∠ABO的度数是°;
②当∠BAD=∠ABD时,x=°;当∠BAD=∠BDA时,x=°.
(2)、如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.