广西壮族自治区崇左市2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-17 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,点(-1,-2)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列各图中,是函数图象的是( ).A、
 B、
B、 C、
C、 D、
D、 3. 下列图形:①三角形,②线段,③正方形,④直角.其中是轴对称图形的个数是( ).A、4个 B、3个 C、2个 D、1个4. 如果 关于 的函数 是正比例函数,那么 的取值范围是( )A、 B、 C、不能确定 D、一切实数5. 在下列命题中,真命题是( )A、同位角相等 B、到线段距离相等的点在线段垂直平分线上 C、三角形的外角和是360° D、角平分线上的点到角的两边相等6. 如图,窗户打开后,用窗钩AB可将其固定,其所运用的几何原理是( )
3. 下列图形:①三角形,②线段,③正方形,④直角.其中是轴对称图形的个数是( ).A、4个 B、3个 C、2个 D、1个4. 如果 关于 的函数 是正比例函数,那么 的取值范围是( )A、 B、 C、不能确定 D、一切实数5. 在下列命题中,真命题是( )A、同位角相等 B、到线段距离相等的点在线段垂直平分线上 C、三角形的外角和是360° D、角平分线上的点到角的两边相等6. 如图,窗户打开后,用窗钩AB可将其固定,其所运用的几何原理是( ) A、三角形的稳定性 B、垂线段最短 C、两点确定一条直线 D、两点之间,线段最短7. 下列条件中,不能判定两个直角三角形全等的是( )A、一锐角和斜边对应相等 B、两条直角边对应相等 C、斜边和一直角边对应相等 D、两个锐角对应相等8. 已知一个等腰三角形两内角的度数之比为 ,则这个等腰三角形顶角的度数为( )A、 B、 C、 或 D、9.
A、三角形的稳定性 B、垂线段最短 C、两点确定一条直线 D、两点之间,线段最短7. 下列条件中,不能判定两个直角三角形全等的是( )A、一锐角和斜边对应相等 B、两条直角边对应相等 C、斜边和一直角边对应相等 D、两个锐角对应相等8. 已知一个等腰三角形两内角的度数之比为 ,则这个等腰三角形顶角的度数为( )A、 B、 C、 或 D、9.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
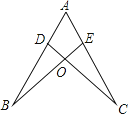 A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD10. 关于直线 ,下列说法正确的是( )A、 经过定点(1,0) B、 经过定点(-1,0) C、 经过第二、三、四象限 D、 经过第一、二、三象限11. 如图是一次函数y1=kx+b与y2=x+a的图象,则下列结论①k<0;②a>0;③当x<3时,kx+b<x+a中,正确的个数是( )
A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD10. 关于直线 ,下列说法正确的是( )A、 经过定点(1,0) B、 经过定点(-1,0) C、 经过第二、三、四象限 D、 经过第一、二、三象限11. 如图是一次函数y1=kx+b与y2=x+a的图象,则下列结论①k<0;②a>0;③当x<3时,kx+b<x+a中,正确的个数是( ) A、0 B、1 C、2 D、312. 如图,∠ABC,∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的是:①△BDF,△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE.( )
A、0 B、1 C、2 D、312. 如图,∠ABC,∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的是:①△BDF,△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE.( )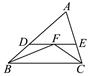 A、③④ B、①② C、①②③ D、②③④
A、③④ B、①② C、①②③ D、②③④二、填空题
-
13. 函数 中自变量x的取值范围是.14. 将直线 沿 轴向上平移6个单位,所得到的直线解析式是 .15. 如图, 是 的中线, , ,那么 的周长比 的周长多 .
 16. 如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为cm.
16. 如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为cm. 17. 如图所示,在 中, , ,且 ,则 .
17. 如图所示,在 中, , ,且 ,则 .
三、解答题
-
18. 如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳)在图中,只要量出 的长,就能求出工件内槽的宽 的长,依据是 .
 19. △ABC在平面直角坐标系中的位置如图所示.
19. △ABC在平面直角坐标系中的位置如图所示.
( 1 )作出△ABC关于y轴对称的△A1B1C1;并写出△A1B1C1各顶点的坐标;
( 2 )将△ABC向右平移6个单位,再向下平移1个单位:作出平移后的△A2B2C2
20. 如图,已知AB=DC,AC=BD,求证:∠B=∠C.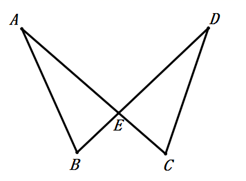 21. 为了保护学生的视力,课桌的高度 与椅子的高度 (不含靠背)都是按 是 的一次函数关系配套设计的,下表列出了两套符合条件课桌椅的高度:
21. 为了保护学生的视力,课桌的高度 与椅子的高度 (不含靠背)都是按 是 的一次函数关系配套设计的,下表列出了两套符合条件课桌椅的高度:第一套
第二套
椅子高度
40.0
37.0
课桌高度
75.0
70.2
(1)、请求出 与 的函数关系式(不要求写出 的取值范围);(2)、现有一把高 的椅子和一张高 的课桌,它们是否配套?请通过计算说明理由.22. “佳园工艺店”打算制作一批有两边长分别是7分米,3分米,第三边长为奇数(单位:分米)的不同规格的三角形木框.(1)、要制作满足上述条件的三角形木框共有种.(2)、若每种规格的三角形木框只制作一个,制作这种木框的木条的售价为8元╱分米,问至少需要多少钱购买材料?(忽略接头)23. 如图,AC是某座大桥的一部分,DC部分因受台风侵袭已垮塌,为了修补这座大桥,需要对DC的长进行测量,测量人员在没有垮塌的桥上选取两点A和D,在C处对岸立着的桥墩上选取一点B(BC⊥AC),然后测得∠A=30°,∠ADB=120°,AD=60 m.求DC的长.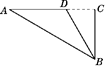 24. 如图,在 中,点 在 边上, , 为 的中点.若 ,求 的度数.
24. 如图,在 中,点 在 边上, , 为 的中点.若 ,求 的度数. 25. 如图, , , ,点 是 的中点, .
25. 如图, , , ,点 是 的中点, . (1)、求证: ;(2)、连结 、 ,试判断 的形状,并证明你的结论.26. 某公司计划购买若干台电脑,现从两家商场了解到同一种型号的电脑报价均为 元,并且多买都有一定的优惠. 各商场的优惠条件如下:
(1)、求证: ;(2)、连结 、 ,试判断 的形状,并证明你的结论.26. 某公司计划购买若干台电脑,现从两家商场了解到同一种型号的电脑报价均为 元,并且多买都有一定的优惠. 各商场的优惠条件如下:甲商场优惠条件:第一台按原价收费,其余的每台优惠 ;
乙商场优惠条件:每台优惠 .
(1)、设公司购买 台电脑,选择甲商场时, 所需费用为 元,选择乙商场时,所需费用为 元,请分别求出 与 之间的关系式.(2)、什么情况下,两家商场的收费相同?什么情况下,到甲商场购买更优惠?什么情况下,到乙商场购买更优惠?(3)、现在因为急需,计划从甲乙两商场一共买入 台某品牌的电脑,其中从甲商场购买 台电脑.已知甲商场的运费为每台 元,乙商场的运费为每台 元,设总运费为 元,在甲商场的电脑库存只有 台的情况下,怎样购买,总运费最少?最少运费是多少?