浙江省台州市2021届九年级下学期数学开学考试试卷
试卷更新日期:2021-03-16 类型:开学考试
一、选择题(本大题有10小题,每小题4分,共40分.请选出每小题中一个最符合题意的选项,不选、多选、错选,均不给分)
-
1. 某自动控制器的芯片,可植入2020000000粒晶体管,这个数字2020000000用科学记数法可表示为A、 B、 C、 D、2. 如图是由四个相同的小正方体组成的立体图形,它的主视图为( ).
 A、
A、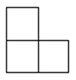 B、
B、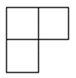 C、
C、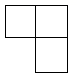 D、
D、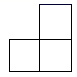 3. 分式 的值是零,则的值为( )A、2 B、5 C、-2 D、-54. 一个不透明的袋子里装有4个红球和2个黄球,它们除颜色外其余都相同.从袋中任意摸出一个球是红球的概率为( )A、 B、 C、 D、5. 如图,在 中, , ,点 在 边上,以 , 为边作▱BCDE,则 的度数为
3. 分式 的值是零,则的值为( )A、2 B、5 C、-2 D、-54. 一个不透明的袋子里装有4个红球和2个黄球,它们除颜色外其余都相同.从袋中任意摸出一个球是红球的概率为( )A、 B、 C、 D、5. 如图,在 中, , ,点 在 边上,以 , 为边作▱BCDE,则 的度数为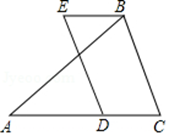 A、 B、 C、 D、6. 如图,把 先向右平移3个单位,再向上平移2个单位得到 ,则顶点 对应点的坐标为
A、 B、 C、 D、6. 如图,把 先向右平移3个单位,再向上平移2个单位得到 ,则顶点 对应点的坐标为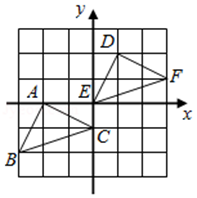 A、 B、 C、 D、7. 在某次演讲比赛中,五位评委给选手圆圆打分,得到互不相等的五个分数.若去掉一个最高分,平均分为x;去掉一个最低分,平均分为 ;同时去掉一个最高分和一个最低分,平均分为z,则A、 B、 C、 D、8. 如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )
A、 B、 C、 D、7. 在某次演讲比赛中,五位评委给选手圆圆打分,得到互不相等的五个分数.若去掉一个最高分,平均分为x;去掉一个最低分,平均分为 ;同时去掉一个最高分和一个最低分,平均分为z,则A、 B、 C、 D、8. 如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( ) A、平行四边形→正方形→平行四边形→矩形 B、平行四边形→菱形→平行四边形→矩形 C、平行四边形→正方形→菱形→矩形 D、平行四边形→菱形→正方形→矩形9. 如图,已知 是 的直径,半径 ,点 在劣弧 上(不与点 ,点 重合), 与 交于点 .设 , ,则
A、平行四边形→正方形→平行四边形→矩形 B、平行四边形→菱形→平行四边形→矩形 C、平行四边形→正方形→菱形→矩形 D、平行四边形→菱形→正方形→矩形9. 如图,已知 是 的直径,半径 ,点 在劣弧 上(不与点 ,点 重合), 与 交于点 .设 , ,则 A、 B、 C、 D、10. 如图,在 中, ,以其三边为边向外作正方形,过点 作 于点 ,再过点 作 分别交边 , 于点 , .若 , ,则 的长为
A、 B、 C、 D、10. 如图,在 中, ,以其三边为边向外作正方形,过点 作 于点 ,再过点 作 分别交边 , 于点 , .若 , ,则 的长为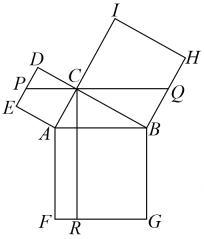 A、14 B、15 C、 D、
A、14 B、15 C、 D、二、填空题(本大题有6小题,每小题5分,共30分)
-
11. 分解因式: .12. 不等式组 的解为 。13. 设 , , .若 , ,则 .14. 小慧用图1中的一副七巧板拼出如图2所示的“行礼图”。已知正方形ABCD的边长为4dm,则图2中h的值为dm。
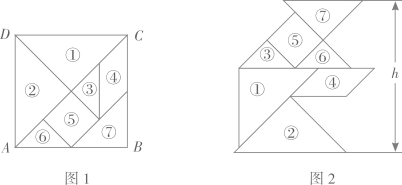 15. 如图,已知边长为2的等边三角形ABC中,分别以点A,C为圆心,m为半径作弧,两弧交于点D,连结BD。若BD的长为2 ,则m的值为。
15. 如图,已知边长为2的等边三角形ABC中,分别以点A,C为圆心,m为半径作弧,两弧交于点D,连结BD。若BD的长为2 ,则m的值为。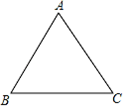 16. 如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使AE⊥l,BF⊥l,点N,A,B在同一直线上。在F点观测A点后,沿FN方向走到M点.观测C点发现∠1=∠2。测得EF=15米,FM=2米,MN=8米,∠ANE=45°,则场地的边AB为米,BC为米。
16. 如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使AE⊥l,BF⊥l,点N,A,B在同一直线上。在F点观测A点后,沿FN方向走到M点.观测C点发现∠1=∠2。测得EF=15米,FM=2米,MN=8米,∠ANE=45°,则场地的边AB为米,BC为米。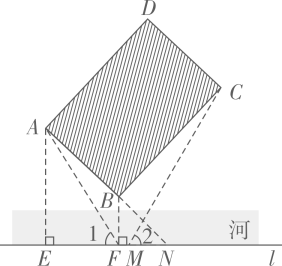
三、解答题(本题有8小题,第17~20题每题8分,第21题10分,第22,23题每题12分,第24题14分,共80分)
-
17.(1)、计算: .(2)、化简: .18. 如图,在 的网格中, 的三个顶点都在格点上.
 (1)、在图1中画出一个以 为边的▱ABDE,使顶点 , 在格点上.(2)、在图2中画出一条恰好平分 周长的直线 (至少经过两个格点).19. 为了解学生对网上在线学习效果的满意度,某校设置了:非常满意、满意、基本满意、不满意四个选项,随机抽查了部分学生,要求每名学生都只选其中的一项,并将抽查结果绘制成如图统计图(不完整).
(1)、在图1中画出一个以 为边的▱ABDE,使顶点 , 在格点上.(2)、在图2中画出一条恰好平分 周长的直线 (至少经过两个格点).19. 为了解学生对网上在线学习效果的满意度,某校设置了:非常满意、满意、基本满意、不满意四个选项,随机抽查了部分学生,要求每名学生都只选其中的一项,并将抽查结果绘制成如图统计图(不完整).请根据图中信息解答下列问题:
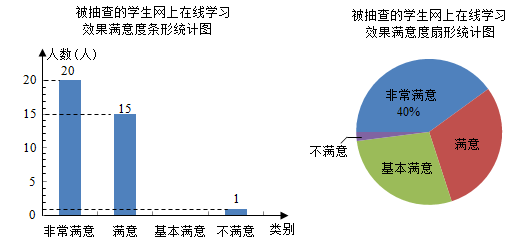 (1)、求被抽查的学生人数,并补全条形统计图;(2)、求扇形统计图中表示“满意”的扇形的圆心角度数;(3)、若该校共有1000名学生参与网上在线学习,根据抽查结果,试估计该校对学习效果的满意度是“非常满意”或“满意”的学生共有多少人?20. 如图,在平面直角坐标系中,二次函数 图象的顶点是 ,与x轴交于 , 两点,与 轴交于点 .点 的坐标是 .
(1)、求被抽查的学生人数,并补全条形统计图;(2)、求扇形统计图中表示“满意”的扇形的圆心角度数;(3)、若该校共有1000名学生参与网上在线学习,根据抽查结果,试估计该校对学习效果的满意度是“非常满意”或“满意”的学生共有多少人?20. 如图,在平面直角坐标系中,二次函数 图象的顶点是 ,与x轴交于 , 两点,与 轴交于点 .点 的坐标是 . (1)、求 , 两点的坐标,并根据图象直接写出当 时的取值范围.(2)、平移该二次函数的图象,使点 恰好落在点 的位置上,求平移后图象所对应的二次函数的表达式.21. 如图1为搭建在地面上的遮阳棚,图2、图3是遮阳棚支架的示意图.遮阳棚支架由相同的菱形和相同的等腰三角形构成,滑块 , 可分别沿等长的立柱 , 上下移动, .
(1)、求 , 两点的坐标,并根据图象直接写出当 时的取值范围.(2)、平移该二次函数的图象,使点 恰好落在点 的位置上,求平移后图象所对应的二次函数的表达式.21. 如图1为搭建在地面上的遮阳棚,图2、图3是遮阳棚支架的示意图.遮阳棚支架由相同的菱形和相同的等腰三角形构成,滑块 , 可分别沿等长的立柱 , 上下移动, .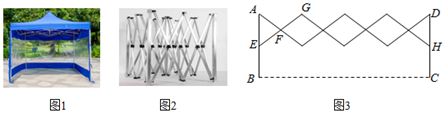 (1)、若移动滑块使 ,求 的度数和棚宽 的长.(2)、当 由 变为 时,问棚宽 是增加还是减少?增加或减少了多少?
(1)、若移动滑块使 ,求 的度数和棚宽 的长.(2)、当 由 变为 时,问棚宽 是增加还是减少?增加或减少了多少?(结果精确到 ,参考数据: , , ,
22. 某经销商3月份用18000元购进一批 恤衫售完后,4月份用39000元购进一批相同的 恤衫,数量是3月份的2倍,但每件进价涨了10元.(1)、4月份进了这批 恤衫多少件?(2)、4月份,经销商将这批 恤衫平均分给甲、乙两家分店销售,每件标价180元.甲店按标价卖出a件以后,剩余的按标价八折全部售出;乙店同样按标价卖出件,然后将 件按标价九折售出,再将剩余的按标价七折全部售出,结果利润与甲店相同.①用含的代数式表示 .
②已知乙店按标价售出的数量不超过九折售出的数量,请你求出乙店利润的最大值.
23. 如图,在 中, ,将 沿直线 翻折得到 ,连接 交 于点 . 是线段 上的点,连接 . 是 的外接圆与 的另一个交点,连接 , . (1)、求证: 是直角三角形;(2)、求证: ;(3)、当 , 时,在线段 上存在点 ,使得 和 互相平分,求 的值.24. 如图,在四边形 中, , , 分别平分 , ,并交线段 , 于点 , (点 , 不重合).在线段 上取点 , (点 在 之间),使 .当点 从点 匀速运动到点 时,点 恰好从点 匀速运动到点 .记 , ,已知 ,当 为 中点时, .
(1)、求证: 是直角三角形;(2)、求证: ;(3)、当 , 时,在线段 上存在点 ,使得 和 互相平分,求 的值.24. 如图,在四边形 中, , , 分别平分 , ,并交线段 , 于点 , (点 , 不重合).在线段 上取点 , (点 在 之间),使 .当点 从点 匀速运动到点 时,点 恰好从点 匀速运动到点 .记 , ,已知 ,当 为 中点时, . (1)、判断 与 的位置关系,并说明理由.(2)、求 , 的长.(3)、若 .
(1)、判断 与 的位置关系,并说明理由.(2)、求 , 的长.(3)、若 .①当 时,通过计算比较 与 的大小关系.
②连结 ,当 所在直线经过四边形 的一个顶点时,求所有满足条件的的值.