浙江省杭州市萧山城区六校2021届九年级下学期数学开学联考试卷
试卷更新日期:2021-03-16 类型:开学考试
一、选择题(本题有10个小题,每小题3分,共30分)
-
1. 已知 (a≠0,b≠0),下列变形正确的是( )A、 B、 C、 D、2. 下列事件中,属于不可能事件的是( )A、掷一枚骰子,朝上一面的点数为5 B、任意画一个三角形,它的内角和是178° C、若实数 ,则 D、在纸上画两条直线,这两条直线互相垂直3. 下列各组图形中,四个顶点一定在同一圆上的是( )A、矩形,菱形 B、矩形,正方形 C、菱形,正方形 D、平行四边形,菱形4. 若二次函数 过P(1,4),则这个函数必过点( )A、(-3,4) B、(-1,4) C、(0,3) D、(2,4)5. 在台风来临之前,有关部门用钢管加固树木(如图),固定点A离地面的高度AC=m,钢管与地面所成角∠ABC=∠ ,那么钢管AB的长为( )
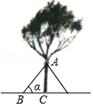 A、m•sin B、m•cos C、 D、6. 若扇形面积为36 ,圆心角为120°,则它的弧长为( )A、 B、 C、 D、7. 如图,在 中,已知 ,E,F分别在边AC,AB上,DE//BC,DF//AC,则( )
A、m•sin B、m•cos C、 D、6. 若扇形面积为36 ,圆心角为120°,则它的弧长为( )A、 B、 C、 D、7. 如图,在 中,已知 ,E,F分别在边AC,AB上,DE//BC,DF//AC,则( ) A、 B、 C、 D、8. 如图,四边形ABCD内接于O,连结对角线AC与BD交于点E,且BD为O的直径,已知∠BDC=40°,∠AEB=110°,则∠ABC=( )
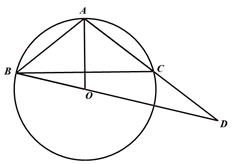
A、 B、 C、 D、8. 如图,四边形ABCD内接于O,连结对角线AC与BD交于点E,且BD为O的直径,已知∠BDC=40°,∠AEB=110°,则∠ABC=( )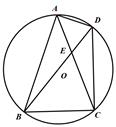 A、65° B、70° C、75° D、80°9. 已知函数 , (a、b、c为常数),如图所示,y2=ax+b.在研究两个函数时,同学们得到结论如下,其中错误的一个结论为( )
A、65° B、70° C、75° D、80°9. 已知函数 , (a、b、c为常数),如图所示,y2=ax+b.在研究两个函数时,同学们得到结论如下,其中错误的一个结论为( )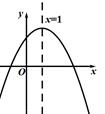 A、 B、当x>3时,ax+b<0 C、当x>2时,y1>y2. D、有两个不同的解10. 如图,已知扇形OAB的半径为r,C是弧AB上的任一点(不与A,B重合),CM⊥OA,垂足为M,CN⊥OB,垂足为N,连接MN,若∠AOB= ,则MN可用 表示为( )
A、 B、当x>3时,ax+b<0 C、当x>2时,y1>y2. D、有两个不同的解10. 如图,已知扇形OAB的半径为r,C是弧AB上的任一点(不与A,B重合),CM⊥OA,垂足为M,CN⊥OB,垂足为N,连接MN,若∠AOB= ,则MN可用 表示为( )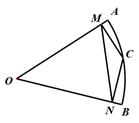 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题有6个小题,每小题4分,共24分)
-
11. 已知一个正多边形的每个内角为120°,则它是正边形.12. 把只有颜色不同的1个白球和2个红球放入不透明的盒子中搅匀,然后从中随机摸出1个球后放回搅匀,再次随机摸出1个球,两次都摸到白球的概率为.13. 一个球从地面上竖直向上弹起的过程中,距离地面高度 (米)与经过的时间 (秒)满足以下函数关系: ,则该球从弹起回到地面需要经过秒,距离地面的最大高度为米.14. 复印纸型号多样,而各型号复印纸之间存在这样的关系:将其中一型号纸张(如A3纸)沿较长边中点的连线对折,就能得到下一型号(A4纸)的纸张,且对折得到的两个矩形和原来的矩形相似(即A3纸与A4纸相似),则这些型号的复印纸宽与长之比为.
 15. 在中,若AB= AC,则 =16. 如图,AB是O的直径,弦CD⊥AB于点E,F是弧BC上任意一点,线段AF与弦CD交于点G,连结FD和AD.
15. 在中,若AB= AC,则 =16. 如图,AB是O的直径,弦CD⊥AB于点E,F是弧BC上任意一点,线段AF与弦CD交于点G,连结FD和AD.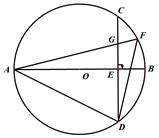 (1)、若 ,则AD=(2)、在(1)的条件下,若CD= ,则O的直径为 .
(1)、若 ,则AD=(2)、在(1)的条件下,若CD= ,则O的直径为 .三、全面答一答(本题有8个小题,共66分)
-
17. 在平面直角坐标中,二次函数 的图像经过点(1,4).(1)、求 的值;(2)、自变量 在什么范围内, 随 增大而增大.18. 甲、乙两人进行摸牌游戏:有三张形状大小完全相同的牌,正面分别标有数字2,3,5。现将三张牌背面朝上,洗匀后放在桌子上。(1)、甲从中随机抽一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表或画树状图的方法,求两人抽取的数字相同的概率.(2)、若两人抽取的数字之和为2的倍数,则甲获胜;若抽取的数字之和为5的倍数,则乙获胜,这个游戏公平吗?请用概率的知识加以解释.19. 如图,为了测出旗杆AB的高度,在旗杆前的平地上一点C,测得旗杆顶部的仰角为45°,在C、B之间选择一点D(B,C,D三点共线),测得旗杆顶部的仰角为75°,且CD=8米.
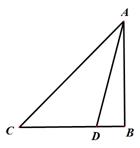 (1)、求D到CA的距离;(2)、求旗杆AB的高度(保留根号).20. 如图,AB是O的直径,四边形ABCD内接于O,OD交AC于点E, = .
(1)、求D到CA的距离;(2)、求旗杆AB的高度(保留根号).20. 如图,AB是O的直径,四边形ABCD内接于O,OD交AC于点E, = .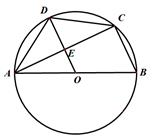 (1)、求证:OD//BC;(2)、若AC=10,DE=4,求BC的长.21. 如图,在△ABC中,点D在边AB上,AD=4.5,BD=3.5.AC=6.△ABC的角平分线AE交CD于点F.
(1)、求证:OD//BC;(2)、若AC=10,DE=4,求BC的长.21. 如图,在△ABC中,点D在边AB上,AD=4.5,BD=3.5.AC=6.△ABC的角平分线AE交CD于点F.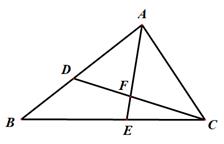 (1)、求证:△ACD∽△ABC;(2)、若AF=4,求AE的长度.
(1)、求证:△ACD∽△ABC;(2)、若AF=4,求AE的长度.