浙江省杭州市萧山城区六校2020-2021学年八年级下学期数学开学联考试卷
试卷更新日期:2021-03-16 类型:开学考试
一、选择题(本题10小题,每小题3分,共30分)
-
1. 下列各点中,在第三象限的点是( )A、 B、 C、 D、2. 在一次函数 的图象上, 随 的增大而减小,则 的取值范围是( )A、 B、 C、 D、3. 已知两条线段a=2cm, b=3.5cm ,下列能和 a、b 构成三角形的是( )A、 B、 C、 D、4. 一个三角形三个内角的度数之比为3:4:5,这个三角形一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形5. 若 ,则 的取值范围是( )A、 B、 C、 D、6. 已知 , 为一次函数 的图像上的两个不同点,且 .若 , ,则 与 的大小关系是( )A、 B、 C、 D、 大小与点的位置有关7. 把一些笔记本分给几个学生,如果每人分3本,那么余8本;如果前面的每个学生分5本,那么最后一人就分不到3本.则共有学生( )A、4人 B、5人 C、6人 D、5人或6人8. 如图,在△ABC中,∠ACB=90°,边AB的垂直平分线交AB于点D,交AC于点E,连接BE,CD,若BC=5,CD=6.5,则△BCE的周长为( )
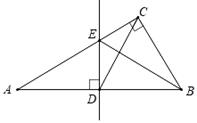 A、16.5 B、17 C、18 D、209. 若关于 的不等式组 的整数解共有3个,则 的取值范围是( )A、 B、 C、 D、10. 甲、乙两位同学住在同一小区,学校与小区相距2700米,一天甲从小区步行出发去学校,12分钟后乙也出发,乙先骑公交自行车,途经学校又骑行一段路到达还车点后,立即步行走回学校.已知步行速度甲比乙每分钟快5米,图中的折线表示甲、乙两人之间的距离 (米)与甲步行时间 (分钟)的函数关系图象,则( )
A、16.5 B、17 C、18 D、209. 若关于 的不等式组 的整数解共有3个,则 的取值范围是( )A、 B、 C、 D、10. 甲、乙两位同学住在同一小区,学校与小区相距2700米,一天甲从小区步行出发去学校,12分钟后乙也出发,乙先骑公交自行车,途经学校又骑行一段路到达还车点后,立即步行走回学校.已知步行速度甲比乙每分钟快5米,图中的折线表示甲、乙两人之间的距离 (米)与甲步行时间 (分钟)的函数关系图象,则( )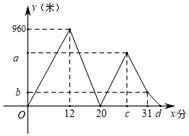 A、乙骑自行车的速度是180米/分 B、乙到还车点时,甲、乙两人相距850米 C、自行车还车点距离学校300米 D、乙到学校时,甲距离学校200米
A、乙骑自行车的速度是180米/分 B、乙到还车点时,甲、乙两人相距850米 C、自行车还车点距离学校300米 D、乙到学校时,甲距离学校200米二、填空题(本题6个小题,每小题4分,共24分)
-
11. 满足 的最大整数是.12. 把点 向右平移3个单位得到的点的坐标为.13. 在 中, , , 是斜边 的中垂线,交 于点 , 的周长为14,则 .14. 已知直线 经过点 ,其中 ,则 .15. .16. 如图,在等腰 中, 分别为 , 边上的点,将边 沿 折叠,使点 落在 上的点 处.当点 与点 重合时, .
三、解答题(本题7个小题,共66分)
-
17. 解不等式,并写出负整数解, .18. 先化简,再求值: ,其中实数 满足 .19. 如图,已知 ,用直尺和圆规作 ,使得 .
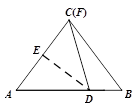
 20. 已知一次函数 .(1)、若图像过点 ,则 是多少;(2)、若它的图像经过一、二、四象限,则 的取值范围是多少;(3)、若直线不经过第四象限,则 的取值范围是多少.21. 如图,在 中, 与点 , 与点 ,且 .
20. 已知一次函数 .(1)、若图像过点 ,则 是多少;(2)、若它的图像经过一、二、四象限,则 的取值范围是多少;(3)、若直线不经过第四象限,则 的取值范围是多少.21. 如图,在 中, 与点 , 与点 ,且 .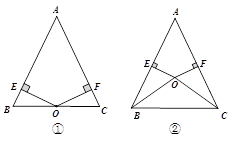 (1)、如图①,当 为 中点时,试说明 ;(2)、如图②,当点 在 内部,且 ,试判断 与 的关系.
(1)、如图①,当 为 中点时,试说明 ;(2)、如图②,当点 在 内部,且 ,试判断 与 的关系.