四川省自贡市2020-2021学年八年级下学期数学开学考试试卷

试卷更新日期：2021-03-16 类型：开学考试

进入出卷网下载

一、选择题（本大题共8小题。每小题3分，共24分.）

1. 若分式 $\frac{1}{x - 1}$ 有意义，则x的取值范围是（）

A、x＞1 B、x≠1 C、x≠0 D、x≠﹣1

查看试题解析
2. 在以下绿色食品、低碳、节能、节水四个标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 在平面直角坐标系中，点（2，5）关于y轴对称点的坐标为（）

A、（﹣2，5） B、（2，﹣5） C、（﹣2，﹣5） D、（2，5）

查看试题解析
4. 某芯片的电子元件的直径为0.0000034米，数0.0000034用科学记数法表示为（）

A、0.34×10^﹣6 B、3.4×10^﹣6 C、34×10^﹣5 D、3.4×10^﹣5

查看试题解析
5. 下列计算正确的是（）

A、b³•b³＝2b³ B、（x+2）（x﹣2）＝x²﹣2 C、（a+b）²＝a²+b² D、（﹣2a）²＝4a²

查看试题解析
6. 已知等腰三角形的两边长分别为3和6，则它的周长等于（　　）

A、12 B、12或15 C、15 D、15或18

查看试题解析
7. 暑假期间，某科幻小说的销售量急剧上升.某书店分别用600元和800元两次购进该小说，第二次购进的数量比第一次多40套，且两次购书时，每套书的进价相同.若设书店第一次购进该科幻小说x套，由题意列方程正确的是（）

A、 $\frac{600}{x} = \frac{800}{x - 40}$ B、 $\frac{600}{x - 40} = \frac{800}{x}$ C、 $\frac{600}{x} = \frac{800}{x + 40}$ D、 $\frac{600}{x + 40} = \frac{800}{x}$

查看试题解析
8. 如图，在等边△ABC中，BD＝CE，将线段AE沿AC翻折，得到线段AM，连结EM交AC于点N，连结DM、CM以下说法：①AD＝AM，②∠MCA＝60°，③CM＝2CN，④MA＝DM中，正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

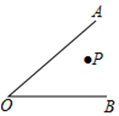
9. 分式 $\frac{3}{2 a^{2} b}$ 与 $\frac{a - b}{a b^{2} c}$ 的最简公分母是.

查看试题解析
10. 计算102×98＝.

查看试题解析
11. 正n边形每个内角的大小都为108°，则n的值为.

查看试题解析
12. 已知 $a - b = 3, a b = 1$ ，则 $a^{2} + b^{2} =$ .

查看试题解析
13. 已知多项式 $x^{2} + 4 x + k^{2}$ 是一个完全平方式，则k的值为.

查看试题解析
14. 如图，P为∠AOB内一点，M，N分别是射线OA，OB上一点，当△PMN周长最小，且∠OPM＝40°时，则∠AOB＝.

查看试题解析

三、解答题（本大题共5小题，共25分）

15. 计算：

(1)、 $3 x • 5 y^{2}$ ；

(2)、 $24 x^{2} y \div (- 6 x y)$ .

查看试题解析
16. 因式分解：

(1)、 $x^{2} - 9$ ；

(2)、 $a x^{2} + 2 a x y + a y^{2}$ .

查看试题解析
17. 解分式方程： $\frac{2}{x + 3} = \frac{1}{x - 1}$ ；

查看试题解析
18. 如图，点B、E、C、F四点在一条直线上，∠A＝∠D，AB //DE，老师说：再添加一个条件就可以使△ABC≌△DEF.下面是课堂上三个同学的发言，甲说：添加AB＝DE；乙说：添加AC //DF；丙说：添加BE＝CF.

(1)、甲、乙、丙三个同学说法正确的是；

(2)、请你从正确的说法中选择一种，给出你的证明.

查看试题解析
19. 先化简，再求值： $（ x + 2 + \frac{5}{2 - x}) • \frac{2 x - 4}{3 - x}$ ，其中 $x = 5$ .

查看试题解析

四、解答题（本大题共3小题，每小题6分，共18分）

20. △ABC在平面直角坐标系中的位置如图所示，先将△ABC向右平移3个长度单位，再向下平移1个长度单位到△A₁B₁C₁ ， △A₁B₁C₁和△A₂B₂C₂关于x轴对称，点A₁、B₁、C₁的对称点分别是点A₂、B₂、C₂.

(1)、画出△A₁B₁C₁和△A₂B₂C₂；

(2)、△ABC的面积为多少？

查看试题解析
21. 甲乙二人做某种机械零件，已知甲每小时比乙多做6个，甲做90个所用时间与乙做60个所用时间相等.求甲、乙每小时各做多少个零件？

查看试题解析
22. 如图，△ABC中，AD⊥BC，EF垂直平分AC，交AC于点F，交BC于点E，且BD＝DE，连接AE.

(1)、若∠BAE＝40°，求∠C的度数；

(2)、若△ABC的周长为14cm，AC＝6cm，求DC长.

查看试题解析

五、解答题（本大题共2小题，23小题7分，24小题8分，共15分）

23. 观察下列方程的特征及其解的特点.
①x＋ $\frac{2}{x}$ ＝－3的解为x₁＝－1，x₂＝－2；

②x＋ $\frac{6}{x}$ ＝－5的解为x₁＝－2，x₂＝－3；

③x＋ $\frac{12}{x}$ ＝－7的解为x₁＝－3，x₂＝－4.

解答下列问题：

(1)、请你写出一个符合上述特征的方程为，其解为x₁＝－4，x₂＝－5；

(2)、根据这类方程特征，写出第n个方程为，其解为x₁＝－n，x₂＝－n－1；

(3)、请利用(2)的结论，求关于x的方程x＋ $\frac{n^{2} + n}{x + 3}$ ＝－2(n＋2)(其中n为正整数)的解.

查看试题解析
24. 如图，在平面直角坐标系中， A，B两点的坐标分别是点A（0，a），点B（b，0），且a，b 满足： ${(a - 6)}^{2} + | b - 6 | = 0$ .

(1)、a=；b=.

(2)、求∠ABO的度数；

(3)、点M为AB的中点，等腰Rt△ODC的腰CD经过点M，∠OCD=90°，连接AD.
① 如图1，求证：AD⊥OD；

② 如图2，取BO的中点N，延长AD交NC于点P，若点P的横坐标为t，请用含t的式子表示四边形ADCO的面积.

查看试题解析