浙江省宁波市镇海区2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-03-16 类型:期末考试
一、单选题
-
1. -3的绝对值是( )A、 B、 C、3 D、-32. 美国约翰斯·霍普金斯大学实时统计数据显示,截至北京时间2020年12月12日,全球新冠肺炎确诊病例超6980万例.其中6980万用科学记数法可以表示为( )A、 B、 C、 D、3. 下列数中:8, , , , ,0, ,0.6666……(数字6无限循环),9.181181118……(相邻两个8之间依次多一个1)无理数有( )A、1个 B、2个 C、3个 D、4个4. 如图,把三角形剪去一个角,所得四边形的周长比原三角形的周长小,能正确解释这一现象的数学知识是( )
 A、四边形周长小于三角形周长 B、两点确定一条直线 C、垂线段最短 D、两点之间,线段最短5. 下面运算正确的是( )A、 B、 C、 D、6. 将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是( )A、
A、四边形周长小于三角形周长 B、两点确定一条直线 C、垂线段最短 D、两点之间,线段最短5. 下面运算正确的是( )A、 B、 C、 D、6. 将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是( )A、 B、
B、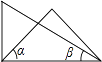 C、
C、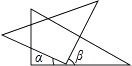 D、
D、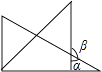 7. 若代数 的值为5,则代数式 的值是( )A、4 B、-1 C、5 D、148. 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.”其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺.则符合题意的方程是( )A、 B、 C、 D、9. 下列说法正确的个数是( )
7. 若代数 的值为5,则代数式 的值是( )A、4 B、-1 C、5 D、148. 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.”其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺.则符合题意的方程是( )A、 B、 C、 D、9. 下列说法正确的个数是( )①射线 与射线 是同一条射线;②点 到点 的距离是线段 ;③画一条长为 的直线;④在同一平面内,过一点有且只有一条直线垂直于已知直线.
A、0个 B、1个 C、2个 D、3个10. 数轴上,点 对应的数是 ,点 对应的数是 ,点 对应的数是0.动点 、 从 、 同时出发,分别以每秒3个单位和每秒1个单位的速度向右运动.在运动过程中,下列数量关系一定成立的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 单项式 的系数是.12. 比较大小: .(填“<”或“>”)13. 用四舍五入法将0.0586精确到千分位,所得到的近似数为14. 一个数的算术平方根是6,则这个数是 , 它的另一个平方根是.15. 一个角的补角比它的余角的3倍少 ,这个角的度数是度.16. 定义一种新运算 ,则 (填计算后结果).17. 如图1,把一个长为m、宽为n的长方形(m>n)沿虚线剪开,拼接成图2,成为在一角去掉一个小正方形后的一个大正方形,则去掉的小正方形的边长(用含m,n的式子表示)为.
 18. 已知以 为未知数的一元一次方程 的解为 ,那么以 为未知数的一元一次方程 的解为.
18. 已知以 为未知数的一元一次方程 的解为 ,那么以 为未知数的一元一次方程 的解为.三、解答题
-
19. 计算:(1)、(2)、20. 解方程:(1)、(2)、21. 先化简,再求值.3a2b﹣[2a2b﹣(2abc﹣a2b)]﹣abc,其中a=﹣2,b=﹣3,c=1.22. 如图,已知点 , , , .按要求画图:

①连接 ,画射线 ;
②画直线 和直线 ,两条直线交于点 ;
③画点 ,使 的值最小.
23. “奶油草莓”是我区湾塘草莓基地的一大特产,现有20筐草莓,以每筐10千克为标准,超过或不足的千克数分别用正、负数来表示,记录如表:与标准质量的差值(单位:千克)
0
0.1
0.25
筐数
1
4
2
3
2
8
(1)、20筐草莓中,与标准质量差值为-0.2千克的有筐,最重的一筐重千克.(2)、若草莓每千克售价40元,则出售这20筐草莓可卖多少元?24. 下表是某网约车公司的专车计价规则计费项目
起租价
里程费
时长费
单价
10元
2.5元/千米
1元/分
注:应付车费=起租价+里程费+时长费,其中起租价10元含5千米里程费和10分钟时长费.
例如:若坐专车行驶里程为12千米,行车时间为20分钟,则需付车费:
(元).
若坐专车行驶里程为4千米,行车时间为12分钟,则需付车费: (元).
(1)、若小聪乘坐专车,行车里程为20千米,行车时间为30分,则需付车费元;(2)、若小聪乘坐专车,行车里程为 ( )千米,平均时速为40千米/时,则小聪应付车费多少元?(用含 的代数式表示)(3)、小聪与小明各自乘坐专车从家去吾悦广场,由于堵车,小聪乘坐了12分钟,小明乘坐了20分钟,两车车费之和为47元,里程之和为15千米(其中小聪的行车里程不超过5千米).那么这两辆专车此次的行驶路程各为多少千米?25. 新定义问题如图①,已知 ,在 内部画射线 ,得到三个角,分别为 、 、 .若这三个角中有一个角是另外一个角的2倍,则称射线 为 的“幸运线”.(本题中所研究的角都是大于 而小于 的角.)
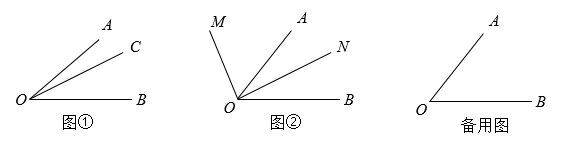 (1)、(阅读理解)
(1)、(阅读理解)角的平分线这个角的“幸运线”;(填“是”或“不是”)
(2)、(初步应用)如图①, ,射线 为 的“幸运线”,则 的度数为;
(3)、(解决问题)如图②,已知 ,射线 从 出发,以每秒 的速度绕 点逆时针旋转,同时,射线 从 出发,以每秒 的速度绕 点逆时针旋转,设运动的时间为 秒( ).若 、 、 三条射线中,一条射线恰好是以另外两条射线为边的角的“幸运线”,求出所有可能的 值.