江苏省镇江市句容市、丹徒区2020-2021学年七年级上学期数学期末考试试卷

试卷更新日期：2021-03-16 类型：期末考试

进入出卷网下载

一、填空题

1. 若 $m$ 的相反数是3，那么 $m =$ ．

查看试题解析
2. 单项式 $- \frac{1}{3} a^{3} b c$ 的次数是．

查看试题解析
3. 在-1.0426中用数字3替换其中的一个非零数字后，使所得的数最大，则被替换的数字是．

查看试题解析
4. 方程 $2 x = - 6$ 和方程 $x + m = - 9$ 的解相同，则 $m$ = ．

查看试题解析
5. 如图，将四边形ABCD沿虚线裁去一个角得到五边形ABCFE ，则该五边形的周长原四边形的周长（填“大于”、“小于”或“等于”）．

查看试题解析
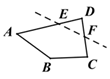6. 若单项式 $a^{m - 1} b^{2}$ 与 $\frac{1}{2} a^{2} b^{n}$ 的和仍是单项式，则 $n^{m}$ 的值是．

查看试题解析
7. 若 $| - x | = 5$ ，则 x的值为．

查看试题解析
8. 已知 $a - 2 b = - 3$ ，则式子 $2021 - a + 2 b =$ ．

查看试题解析
9. 若一个多项式与 $m - n$ 的和等于2m ，则这个多项式是．

查看试题解析
10. 如图，直线AB与CD相交于点O ， $O M ⊥ A B$ ，若 $∠ D O M = 55 °$ ，则 $∠ A O C$ =°．

查看试题解析
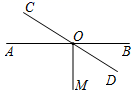11. 如图，有一根木棒A B的两端放置在数轴上，A、B两端分别落在数轴上的数为a、b ．若将木棒沿左端在数轴上翻转，翻转后右端B的对应点 $B^{'}$ 落在数轴上-1.5处；若将木棒沿右端在数轴上翻转，翻转后左端A的对应点 $A^{'}$ 落在数轴上7.5处．由此可得，木棒AB长为cm．

查看试题解析
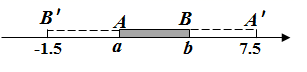12. G101是一班从北京南站开往上海虹桥的下行（单向）高速列车，停靠如图所示的11个站点，则该趟列车共有个乘车区间（指旅客乘车地与目的地之间的区间）．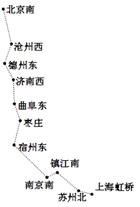

查看试题解析

二、单选题

13. 根据美国约翰斯·霍普金斯大学统计的数据，截至美国东部时间2020年12月31日17时美国新冠肺炎确诊病例总数已超过1989万例.1989万用科学记数法可表示为（）

A、 $19.89 \times 10^{2}$ 万 B、 $1.989 \times 10^{3}$ 万 C、 $0.1989 \times 10^{4}$ 万 D、 $1.9 \times 10^{3}$ 万

查看试题解析
14. 下列运算中，结果正确的是（）

A、 $3 a^{2} + 4 a^{2} = 7 a^{4}$ B、 $4 m^{2} n + 2 m n^{2} = 6 m^{2} n$ C、 $2 x^{2} - \frac{1}{2} x^{2} = \frac{3}{2} x^{2}$ D、 $2 a - a = 2$

查看试题解析
15. 如图所示为我市2021年1月11日的天气预报图，则这天的温差是（）

A、 $- 6 ° C$ B、 $- 2 ° C$ C、 $4 ° C$ D、 $6 ° C$

查看试题解析
16. 实效m，n在数轴上的对应点如图所示，则下列各式子正确的是（）

A、 $m > n$ B、 $- n > | m |$ C、 $- m > | n |$ D、 $| m | < | n |$

查看试题解析
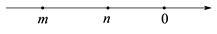17. 如图是一副三角板摆成的图形，如果 $∠ A O B = 160 °$ ，那么 $∠ C O D$ 等于（）

A、15° B、20° C、30° D、40°

查看试题解析
18. 两个同样大小的正方体按如图的方式放在一起，每个正方体相对两个面上写的数字之和都等于0．现将两个正方体并排放置，看得见的5个面上的数如图所示，则看不见的7个面上所写的数字之和等于（）

A、-5 B、-7 C、5 D、无法确定

查看试题解析
19. 用手指计数常对较小的数比较方便，但如果有一定的规律，也能表示较大的数．如图为手的示意图，在各个手指间标记字母A、B、C、D ，请你按图中箭头所指方向（即 $A \to B \to$ $C \to D \to C \to B \to A \to B \to C \to$ …的方式）从A开始数连续的正整数1，2，3，4…，当字母 $C$ 第2021次出现时，恰好数到的数是（）

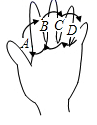A、8087 B、6063 C、4045 D、2021

查看试题解析

三、解答题

20. 计算或化简：

(1)、18－6÷(－3)×(－2)

(2)、 $- 1^{4} - [2 - {(- 3)}^{2}]$

(3)、先化简再代入求值： $(4 a^{2} - 3 a) - 2 (1 - 2 a + 2 a^{2})$ ，其中 $a = - 2$ ．

查看试题解析
21. 解方程：

(1)、 $3 - (x + 2) = 5 (x + 1)$ ；

(2)、 $\frac{2 x - 1}{3} = \frac{3 x - 5}{4} + 1$

查看试题解析
22. 如图，若干个完全相同的小正方体堆成一个几何体．

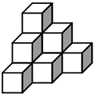
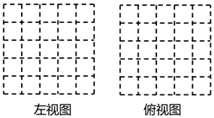(1)、请在图中方格中画出该几何体的左视图和俯视图．

(2)、用若干小立方体搭一个几何体，使得它的左视图和俯视图与你在方格中所画的一致，则这样的几何体最多要个小立方块．

(3)、若小正方体的棱长为 $1 c m$ ，如果将图1中几何体的表面（不含几何体之间叠合部分及与地面接触的底面）喷上油漆，求需喷漆部分的面积．

查看试题解析
23. 如图，点C为线段AD上一点，点B为CD的中点，且 $A C = 4 B C$ ， $A B = 10 cm$ ．

(1)、求线段AD的长；

(2)、若点E在直线AD上，且 $E A = 3 cm$ ，则线段BE=cm．

查看试题解析
24. 下面是某校七年级数学课外活动小组的两位同学对话，根据对话内容求这个课外活动小组现在的人数．

查看试题解析
25. 一般情况下，对于数m和n（ $m n \neq 0$ ）， $\frac{m}{3} + \frac{n}{6} \neq \frac{m + n}{3 + 6}$ (≠表示不等号)，但是对于某些特殊的数m和n（ $m n \neq 0$ ），能使等式 $\frac{m}{3} + \frac{n}{6} = \frac{m + n}{3 + 6}$ 成立，我们把这些特殊的数m和n称为等式 $\frac{m}{3} + \frac{n}{6} = \frac{m + n}{3 + 6}$ 的“分型数对”，记作 $< m ， n >$ ．例如当 $m = 1 ， n = - 4$ 时，有 $\frac{m}{3} + \frac{n}{6} = \frac{m + n}{3 + 6}$ ，那么 $1 ， - 4$ 就是等式 $\frac{m}{3} + \frac{n}{6} = \frac{m + n}{3 + 6}$ “分型数对”．

(1)、 $〈 - 2 ， 6 〉$ ， $〈 5 ， - 20 〉$ 可以称为等式 $\frac{m}{3} + \frac{n}{6} = \frac{m + n}{3 + 6}$ “分型数对”的是；

(2)、如果 $〈 2 ， x 〉$ 是等式的 $\frac{m}{3} + \frac{n}{6} = \frac{m + n}{3 + 6}$ “分型数对”，求 $x$ 的值；

(3)、若 $〈 a ， b 〉$ 是等式的 $\frac{m}{3} + \frac{n}{6} = \frac{m + n}{3 + 6}$ “分型数对”（ $a b \neq 0$ ），求代数式 $(6 a + 3 b - 3) - (b - 2 a - 1)$ 的值．

查看试题解析
26. 2020年春，新型冠状病毒疫情在我国局部扩散．为响应习近平总书记“人民至上、生命至上”要求，某厂紧急改造两个车间生产医用外科口罩，已知甲车间比乙车间每天少生产1万只，甲车间和乙车间共同生产5天可完成35万只．

(1)、求甲车间和乙车间每天各生产口罩多少万只？

(2)、为了应对疫情的发展，甲、乙两车间后来优化了生产工艺，口罩每天的生产量比原来提高10%，则甲、乙两车间现在共同完成308万只口罩的生产时间要比原来缩短几天．

查看试题解析
27. 如图1，点O为直线AB上一点，点C是位于直线AB上方的一点，且∠BOC=20° ，将一个含60°三角板（∠POQ=60°）顶点放在点O处，一边OP与射线OA重合，点Q在直线AB的上方．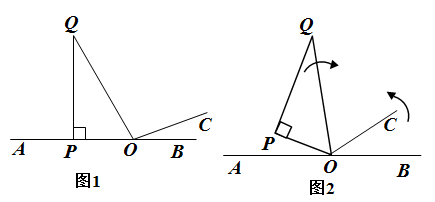

(1)、∠QOC=°

(2)、如图2，现将图1位置中三角板△OPQ绕点O沿顺时针方向每秒转动8° ，射线OC绕点O沿逆时针方向每秒转动12° ，设转动的时间为t秒，当点Q、点C有一点位于直线AB上时，转动停止．
①当线段OQ与射线OC重合时，求t的值；

②当t=时，OP⊥OC ．

查看试题解析