江苏省泰州市海陵区2020-2021学年七年级上学期数学期末考试试卷

试卷更新日期：2021-03-16 类型：期末考试

进入出卷网下载

一、单选题

1. ﹣5的倒数是（）

A、 $\frac{1}{5}$ B、5 C、﹣ $\frac{1}{5}$ D、﹣5

查看试题解析
2. 信息来自国家卫生健康委员会官方网站：截至2020年12月14日24时，据31个省（自治区、直辖市）和新疆生产建设兵团报告，现有确诊“新冠”病例312例（其中重症病例7例），累计治愈出院病例81812例.将81812用科学记数法表示为（）

A、818.12×10² B、81.812×10³ C、8.1812×10⁴ D、0.81812×10⁵

查看试题解析
3. 下列每组数分别是三根小木棒的长度，不能用它们搭成三角形的是（）

A、1cm，2cm，3cm B、2cm，3cm，4cm C、3cm，4cm，5cm D、5cm，6cm，7cm

查看试题解析
4. 若x＝－1是关于x的方程2x＋3a＋1＝0的解，则3a＋1的值为（）

A、0 B、－2 C、2 D、3

查看试题解析
5. 如图，直线a，b被直线c所截，下列条件能判断a∥b的是（）

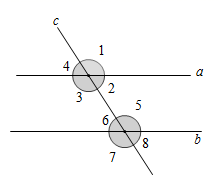A、∠3＝∠5 B、∠4＝∠7 C、∠2＋∠3＝180° D、∠1＝∠3

查看试题解析
6. 已知在数轴上，点A表示的数为x₁ ，点B表示的数为x₂ ，点O表示的数为0，且x_l ＜0＜ x₂ ， $| x_{2} | = 2 | x_{1} |$ ，则（）

A、AO＋ $\frac{1}{2}$ AB＝2BO B、BO＝ $\frac{1}{2}$ AB C、2AO＋ $\frac{1}{2}$ BO ＝AB D、BO＝ $\frac{1}{3}$ AB

查看试题解析

二、填空题

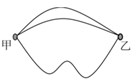
7. 从甲地到乙地有3条路，但小明说这三条路都不是最短的，小明的依据是.

查看试题解析
8. 若单项式 $2 x^{2} y^{m}$ 与 $3 x^{n} y^{3}$ 是同类项，则 $m + n$ 的值是.

查看试题解析
9. 请写出一个三视图相同的几何体：.

查看试题解析
10. 如图，∠1＝30°，则射线OA表示的方位是南偏东.

查看试题解析
11. 若x²＝4，则x＝.

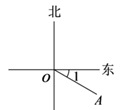查看试题解析
12. 若 $(m - 1) x^{| m |} + 3 = 0$ 是关于x的一元一次方程，则m的值是.

查看试题解析
13. 我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题：“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？”意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完，试问大、小和尚各多少人？设大和尚有 $x$ 人，依题意列方程得.

查看试题解析
14. 如图，纸板上有19个无阴影的小正方形，从中选涂1个，使它与图中5个有阴影的小正方形一起能折叠成一个正方体纸盒，一共有种选法.

查看试题解析
15. 若△ABC三条边长为a，b，c，化简： $| a + b - c | - | a - c - b |$ ＝.

查看试题解析
16. 若点C为线段AB上一点，AB＝6，AC＝4，点D为直线AB上一点，M、N分别是AB、CD的中点，若MN＝5，则线段AD的长为.

查看试题解析

三、解答题

17. 计算：

(1)、14－25＋13

(2)、 $- 1^{4} - | 2 - 3 | + {(- \frac{1}{2})}^{2} \times 8 \div \frac{1}{3}$

查看试题解析
18. 解方程：

(1)、 $1 - \frac{1 - x}{2} = \frac{2 x - 1}{3}$

(2)、 $5 x - 8 = 8 x + 1$

查看试题解析
19. 先化简，再求值： $5 (3 a^{2} b - a b^{2}) - 4 (3 a^{2} b - a b^{2})$ ，其中 a＝－1，b＝2

查看试题解析
20. 如图，在6×6的正方形网格中，每个小正方形的边长都为1

（ 1 ）在图中确定三角形顶点A，B，C的位置，使AB＜BC＜CA.

（ 2 ）利用网格，作△ABC的高线CD.

（ 3 ）△ABC的面积为▲ .

查看试题解析
21. 如图，∠ABC与∠DEF的两边分别交于点M、N.若∠ABC＝∠DEF，且AB∥EF.试说明BC∥DE.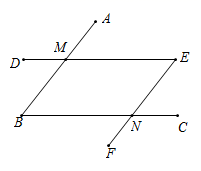

查看试题解析
22. 小明和小丽两人同时从A地出发去B地.小丽的速度为4 km/h，小明的速度为5 km/h，小丽比小明晚到15 min.求A、B两地之间的路程.

查看试题解析
23. 有若干个完全相同的小正方体堆成一个如图所示几何体.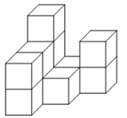

(1)、图中共有个小正方体.

(2)、画出该几何体的主视图、左视图、俯视图.

(3)、若现在你手头还有一些相同的小正方体，如果保持俯视图和左视图不变，最多可以再添加个小正方体.

查看试题解析
24. 如图，点O在直线AB上，CO⊥AB，∠2—∠1＝34°，OE是∠BOD的平分线，OF⊥OE.

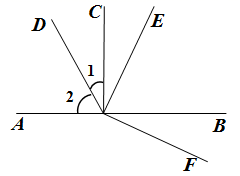(1)、求∠BOE的度数.

(2)、找出图中与∠BOF相等的角，并求出它的度数.

查看试题解析
25. 如图，在△ABC中，BD、CD分别平分∠ABC、∠ACB，点M、N、Q分别在AB、AC、BC的延长线上，BE、CE分别平分∠MBC、∠NCB.

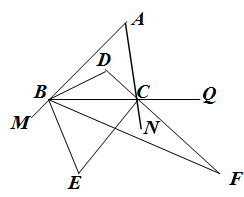(1)、若∠A＝60°
①∠BDC的度数为 .

②求∠BEC的度数.

(2)、如图，若在∠EBC内部作∠EBF，使 $∠ E B F = \frac{2}{3} ∠ E B C$ ，在∠ECQ内部作∠ECF，使 $∠ E C F = \frac{2}{3} ∠ E C Q$ ，则∠BEC和∠BFC有什么样的数量关系？请简述理由.

查看试题解析
26. 如图1，数轴上点A表示的数为－2，点B 表示的数为6，点P从点A出发以每秒1个单位长度的速度沿数轴向右匀速运动，点Q从点B出发以每秒3个单位长度的速度沿数轴向左匀速运动，点M、N分别为PA、QB的中点.P、Q两点同时出发，当点P到达点B时，运动停止，设点P、Q运动时间为t秒.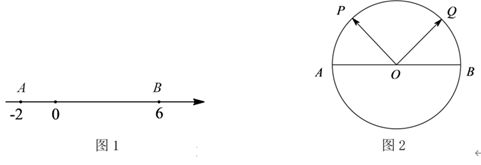

(1)、当点P、Q相遇时，t ＝， MN ＝.

(2)、当PQ之间的距离为4个单位长度时，求线段MN的长.

(3)、[知识迁移]学校数学社团学员自制了一个圆形转盘，如图2，O为转盘圆心，A、O、B在一条直线上，指针OP从OA出发绕点O顺时针方向转动，指针OQ也以相同的速度从OB出发绕点O逆时针方向转动.OP、OQ同时出发，当OP、OQ分别到达OB、OA时，运动停止.已知OM平分∠AOP，ON平分∠BOQ，设∠MON ＝ α，∠POQ ＝ β.试探索α与β的关系.（直接写出答案）

查看试题解析