江苏省苏州市吴中区校2021届九年级下学期数学开学考试试卷
试卷更新日期:2021-03-16 类型:开学考试
一、单选题
-
1. 把一元二次方程 化成一般形式,则a,b,c的值分别是( )A、 B、 C、 D、2. 方程 的根为( )A、0或-2 B、-2 C、0 D、1或-13. 对于二次函数 的图象,下列说法正确的是( )A、开口向下 B、对称轴是直线 C、顶点坐标是(2,1) D、与 轴有两个交点4. 在Rt△ABC中,∠ACB = 90°,AC = 9,BC = 12,则其外接圆的半径为( )
 A、15 B、7.5 C、6 D、35. 如图,点A,B,C在 上,且 ,则 的度数是( )
A、15 B、7.5 C、6 D、35. 如图,点A,B,C在 上,且 ,则 的度数是( )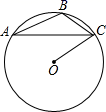 A、 B、 C、 D、6. 如图,在扇形 中,已知 , ,过 的中点C作 , ,垂足分别为D、E,则图中阴影部分的面积为( )
A、 B、 C、 D、6. 如图,在扇形 中,已知 , ,过 的中点C作 , ,垂足分别为D、E,则图中阴影部分的面积为( ) A、 B、 C、 D、7. 关于 的一元二次方程 有一个实数根 ,则下面关于该方程的判别式 的说法正确的是( )A、 B、 C、 D、无法确定8. 书架上摆放有5本书,其中2本教科书,3本文学书,任意从书架上抽取1本,抽到教科书的概率是( )A、 B、 C、 D、9. 若二次函数y=ax2+1的图象经过点(-2,0),则关于x的方程a(x-2)2+1=0的实数根为( )A、 , B、 , C、 , D、 ,10. 已知点O是 的外心,作正方形 ,下列说法:①点O是 的外心;②点O是 的外心;③点O是 的外心;④点O是 的外心.其中说法一定正确的是( )A、②④ B、①③ C、②③④ D、①③④
A、 B、 C、 D、7. 关于 的一元二次方程 有一个实数根 ,则下面关于该方程的判别式 的说法正确的是( )A、 B、 C、 D、无法确定8. 书架上摆放有5本书,其中2本教科书,3本文学书,任意从书架上抽取1本,抽到教科书的概率是( )A、 B、 C、 D、9. 若二次函数y=ax2+1的图象经过点(-2,0),则关于x的方程a(x-2)2+1=0的实数根为( )A、 , B、 , C、 , D、 ,10. 已知点O是 的外心,作正方形 ,下列说法:①点O是 的外心;②点O是 的外心;③点O是 的外心;④点O是 的外心.其中说法一定正确的是( )A、②④ B、①③ C、②③④ D、①③④二、填空题
-
11. 方程 的解为 .12. 二次函数 的图象的顶点坐标为.13. 若关于x的方程 有一个根是1,则 .14. 已知 的半径为 , ,则点P在 的.(填“上面”“内部”或“外部”)15. 如图,已知 是 的直径, 是 的切线,连接 交 于点D,连接 .若 ,则 的度数是 .
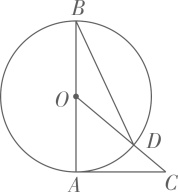 16. 圆锥的母线长为 ,侧面积为 ,则圆锥的底面圆半径 .17. 若关于x的一元二次方程 有实数解,则m的取值范围是.18. 如图,在 中, , , ,P是 所在平面内一点,且满足 ,则 的最大值为.
16. 圆锥的母线长为 ,侧面积为 ,则圆锥的底面圆半径 .17. 若关于x的一元二次方程 有实数解,则m的取值范围是.18. 如图,在 中, , , ,P是 所在平面内一点,且满足 ,则 的最大值为.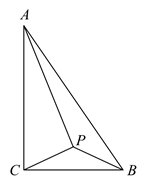
三、解答题
-
19. 计算: .20. 解方程:(1)、 ;(2)、 .21. 已知关于x的一元二次方程 .(1)、求证:方程有两个不相等的实数根;(2)、若 的两边 , 的长是这个方程的两个实数根,第三边 的长为5,当 是直角三角形时,求k的值.22. 若二次函数 的图象经过点(1,0)和点(2,1).(1)、求a、b的值;(2)、写出该二次函数的对称轴和顶点坐标.23. 某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
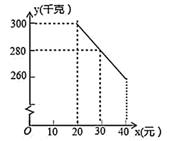 (1)、求y与x的函数解析式;(2)、设该水果销售店试销草莓获得的利润为W元,求W的最大值.24. 如图, 中, ,且 ,以 为直径作 ,点D为 上一点,且 .连接 并延长交 的延长线于点E.
(1)、求y与x的函数解析式;(2)、设该水果销售店试销草莓获得的利润为W元,求W的最大值.24. 如图, 中, ,且 ,以 为直径作 ,点D为 上一点,且 .连接 并延长交 的延长线于点E.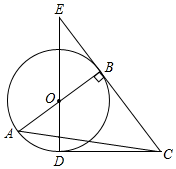 (1)、判断直线 与 的位置关系,并说明理由;(2)、求 的面积.25. 如图,抛物线 与x轴交于A,B两点,与y轴交于点C,直线 经过点C.线段 在线段 上移动,点P的横坐标为t, ,分别过点P,Q作x轴的垂线,交抛物线于E,F两点,交直线 于D,G两点.
(1)、判断直线 与 的位置关系,并说明理由;(2)、求 的面积.25. 如图,抛物线 与x轴交于A,B两点,与y轴交于点C,直线 经过点C.线段 在线段 上移动,点P的横坐标为t, ,分别过点P,Q作x轴的垂线,交抛物线于E,F两点,交直线 于D,G两点.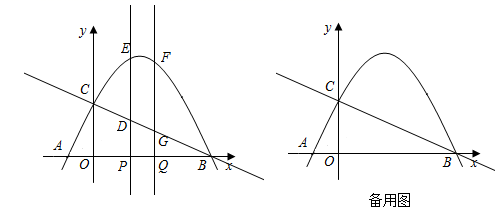 (1)、求抛物线的解析式;(2)、是否存在实数t,使得 ?如果存在,请求出相应的t的值;如果不存在,请说明理由.26. 请认真阅读下列材料:
(1)、求抛物线的解析式;(2)、是否存在实数t,使得 ?如果存在,请求出相应的t的值;如果不存在,请说明理由.26. 请认真阅读下列材料:如图①,给定一个以点O为圆心,r为半径的圆,设点A是不同于点O的任意一点,则点A的反演点定义为射线 上一点 ,满足 .
显然点A也是点 的反演点.即点A与点 互为反演点,点O为反演中心,r称为反演半径.这种从点A到点 的变换或从点 到点A的变换称为反演变换.

例如:如图②,在平面直角坐标系中,点 ,以点O为圆心, 为半径的圆,交y轴的正半轴于点B;C为线段 的中点,P是 上任意一点,点D的坐标为 ;若C关于 的反演点分别为 .
( 1 )求点 的坐标;
( 2 )连接 、 ,求 的最小值.
解:( 1 )由反演变换的定义知: ,其中 , .
∴ ,故点 的坐标为 ;
( 2 )如图③,连接 、 ,由反演变换知 ,
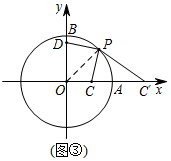
即 ,而 ,
∴ .
∴ ,即 .
∴ .
故 的最小值为13.
请根据上面的阅读材料,解决下列问题:
如图④,在平面直角坐标系中,点 ,以点O为圆心, 为半径画圆,交y轴的正半轴于点B,C为线段 的中点,P是 上任意一点,点D的坐标为 .

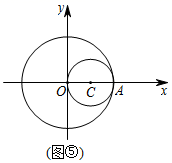 (1)、点D关于 的反演点 的坐标为;(2)、连接 、 ,求 的最小值;(3)、如图⑤,以 为直径作 ,那么 上所有的点(点O除外)关于 的反演点组成的图形具有的特征是.
(1)、点D关于 的反演点 的坐标为;(2)、连接 、 ,求 的最小值;(3)、如图⑤,以 为直径作 ,那么 上所有的点(点O除外)关于 的反演点组成的图形具有的特征是.