重庆市万州区2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-03-16 类型：期末考试

进入出卷网下载

一、单选题

1. 在下列实数中，无理数是（）

A、 $- \frac{5}{3}$ B、 $\sqrt{8}$ C、-2 D、5

查看试题解析
2. 下列运算正确的是（）

A、 $x^{2} \cdot x^{4} = x^{6}$ B、 ${(x^{2})}^{4} = x^{6}$ C、 $x^{3} + x^{3} = 2 x^{6}$ D、 ${(- 2 x)}^{3} = - 6 x^{3}$

查看试题解析

3. 万州区2020年初中数学优质课比赛有11位选手参加，成功在南京中学举行，要适时公布每位选手的成绩，采用的是下面的方法公布的选手成绩，则它是（）

选手序号	1	2	3	4	5	6	7	8	9	10	11
成绩	*	*	*	*	*	*	*	*	*	*	*

A、条形统计图 B、扇形统计图 C、折线统计图 D、统计表

查看试题解析

4. 如图，已知AB=AC，BD=DC，则直接能使△ABD≌△ACD的根据是（）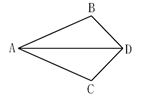

A、SAS B、ASA C、AAS D、SSS

查看试题解析
5. 若 $\sqrt{a - 5} + {(b + 3)}^{2} = 0$ ，则 $a 、 b$ 的值分别为（）

A、5、3 B、5、-3 C、-5、-3 D、-5、3

查看试题解析
6. 估算 $6 - \sqrt{5}$ 的值，它的整数部分是（）

A、2 B、3 C、4 D、5

查看试题解析
7. 若 $△ A B C$ 的三边为下列四组数据，则能判断 $△ A B C$ 是直角三角形的是（）

A、1、2、2 B、2、3、4 C、6、7、8 D、6、8、10

查看试题解析
8. 下列命题的逆命题一定成立的是（）

A、在三角形中，等边对等角 B、全等三角形的对应角相等 C、若 $a = b$ ，则 $| a | = | b |$ D、若 $x = 2$ ，则 $x^{2} - 2 x = 0$

查看试题解析
9. 如图，DE是AC的垂直平分线，CE=5，△BDC的周长为15，则△ABC的周长是（）

A、15 B、20 C、25 D、30

查看试题解析
10. 如图，都是由同样大小的五角星按一定的规律组成，其中第①个图形一共有2个五角星，第②个图形一共有8个五角星，第③个图形一共有18个五角星，…，则第⑨个图形中五角星的个数为（）

A、72个 B、98个 C、128个 D、162个

查看试题解析
11. 如图，从边长为 $2 a + 1$ 的正方形纸片中剪去一个边长为 $a + 2$ 的正方形 $(a > 0)$ ，剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙），则矩形的面积为（）

A、 $3 a^{2} - 3$ B、 $3 a^{2} + 3$ C、 $a^{2} - 2 a + 1$ D、 $a^{2} + 18 a + 9$

查看试题解析
12. 已知 $x 、 y 、 z$ 满足 $x - z = 12$ ， $x z + y^{2} = - 36$ ，则 $x + 2 y + z$ 的值为（）

A、4 B、1 C、0 D、-8

查看试题解析

二、填空题

13. 分解因式 $a^{3} - 3 a^{2}$ =.

查看试题解析
14. 一组数据经整理后分成五组，第一，二，三，四小组的频率分别为0.1，0.1，0.3，0.2，若第二小组的频数是6，则第五小组的频数是.

查看试题解析
15. 计算： $| - 6 | + \sqrt[3]{- 125} + \sqrt{16}$ =.

查看试题解析
16. 若 $a^{2} + m a + 36$ 是一个关于 $a$ 的完全平方式，则 $m =$ .

查看试题解析
17. 如图，在△ABC中，AD平分∠BAC，交BC于点D，BE⊥AD于E，AB=6，AC=14，∠ABC=3∠C，则BE=.

查看试题解析
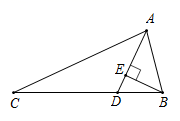18. 如图，△ABC中（AB＞BC），G在CB的延长线上，边AC的垂直平分线DE与∠ABG的角平分线交于点M，与AB交于点D，与AC相交于E，MN⊥AB于N.已知AB=13，BC=9，MN=3，则△BMN的面积是.

查看试题解析

三、解答题

19. 化简求值： $[(a + 3 b) (- a + 3 b) - {(2 a - 3 b)}^{2} + 5 a (4 b - a)] \div (2 a)$ ，其中 $a = 2, b = - \frac{1}{2}$ .

查看试题解析
20. 如图，已知：点B、F、C、E在一条直线上，∠B=∠E，AC=DF， $A C // D F$ .

(1)、求证：△ABC≌△DEF；

(2)、若BF=6，求CE的长.

查看试题解析
21. 垃圾的分类处理与回收利用，可以减少污染，节省资源.重庆主城区环保部门为了提高宣传实效，抽样调查了部分居民小区一段时间内生活垃圾的分类情况（全部分类），其相关信息如图表，根据图表解答下列问题：

(1)、请将条形统计图补充完整；

(2)、在抽样数据中，产生的有害垃圾共吨；

(3)、调查发现，在可回收物中塑料类垃圾占20%，每回收1吨塑料类垃圾可获得0.7吨二级原料.若重庆主城区某月产生的生活垃圾为300000吨，且全部分类处理，那么该月回收的塑料类垃圾可以获得多少吨二级原料？

查看试题解析
22. “某市道路交通管理条例”规定：小汽车在城市街路上行驶速度不得超过40千米/时，如图，一辆小汽车在一条城市街路上直道行驶，某一时刻刚好行驶到路面对车速检测仪A正前方18米的C处，过了2秒后到达B处（BC⊥AC），测得小汽车与车速检测仪间的距离AB为30米，请问这辆小汽车是否超速？若超速，则超速了多少？

查看试题解析
23. 小琪、小米两人在计算一道整式乘法题 $(3 m + a) (2 m - b)$ 时，小琪由于把第二个多项式中的“ $2 m$ ”看成了“ $3 m$ ”，得到的结果为 $9 m^{2} - 3 m - 6$ ，小米由于把第一个多项式中的“ $+ a$ ”看成了“ $+ 2 a$ ”，得到的结果为 $6 m^{2} - m - 12$ .

(1)、求的 $a 、 b$ 的值；

(2)、求出此题的正确结果.

查看试题解析
24. 把一个三位自然数（或两位自然数）各数位上最大的数字的平方依次减去其它数位上的数字的平方所得的差，再取绝对值，得到一个新数，叫做第一次运算（规定：新数为两位数或0，得到0时即停止运算），再把所得新数的一个数位上的数字的平方减去另一个数位上的数字的平方的差，再取绝对值，又得到一个新数，叫做第二次运算，……如此重复下去，若最终结果为0，我们就把具有这种特征的三位或两位自然数称为“完美数”.例如：
$117 \to | 7^{2} - 1^{2} - 1^{2} | = 47 \to | 7^{2} - 4^{2} | = 33 \to | 3^{2} - 3^{2} | = 0 ，$ $506 \to | 6^{2} - 0^{2} - 5^{2} | = 11 \to | 1^{2} - 1^{2} | = 0 ， 22 \to | 2^{2} - 2^{2} | = 0 ，$ 所以117、506、22是“完美数”.

(1)、704“完美数”（填“是”或“不是”）；最大的三位“完美数”是；并说明496为“完美数”.

(2)、若一个两位“完美数”经过两次运算后结果为0，且把这个两位“完美数”与它的各位上的数字的和相加所得的数除以6余1，求出满足这个条件的所有的两位“完美数”.

查看试题解析
25. 如图所示，△ABC中，AB=BC，DE⊥AB于点E，交AC于D，EF⊥BC于点F.

(1)、若∠CDE=152°，求∠DEF的度数；

(2)、若点D是AC的中点，求证： $∠ A B C = 2 ∠ A D E$ .

查看试题解析
26. 已知，点P是Rt△ABC斜边AB上一动点（不与A、B重合），分别过A、B向直线CP作垂线，垂足分别为D、E，M为斜边AB的中点（备注，可以直接用结论：直角三角形斜边上的中线等于斜边的一半）.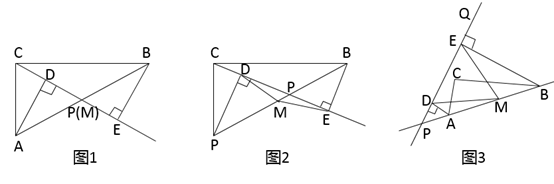

(1)、如图1，当点P与点M重合时，AD与BE的位置关系是， MD与ME的数量关系是.

(2)、如图2，当点P在线段AB上不与点M重合时，试判断MD与ME的数量关系，并说明理由；

(3)、如图3，当点P在线段BA的延长线上且PQ是不与AB重合的任一直线时，分别过A、B向直线PQ作垂线，垂足分别为D、E，此时（2）中的结论是否成立？若成立，请说明理由.

查看试题解析