陕西省宝鸡市凤翔县2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-16 类型:期末考试
一、单选题
-
1. 下列各组数是勾股数的是( )A、0.3,0.4,0.5 B、7,8,9 C、6,8,10 D、 , ,2. 在实数:3.141 59, ,1.010 010 001, , ,π, , 中,无理数有( )
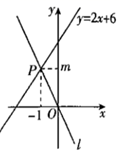
A、4个 B、1个 C、3个 D、2个3. 下列说法错误的是( )A、 的立方根是 B、1的平方根是1 C、 是5的平方根 D、0是0的平方根4. 在平面直角坐标系中,若点 在第二象限,则 的取值范围为( )A、 B、 C、 D、5. 如图,矩形ABCD的边AD长为2,AB长为1,点A在数轴上对应的数是-1,以A点为圆心,对角线AC长为半径画弧,交数轴于点E , 则点E表示的实数是( )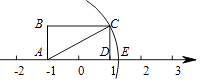 A、 +1 B、 -1 C、 D、1-6. 下列各式是二次根式的个数有 ; ; ; ( ); ; ( )A、3个 B、4个 C、5个 D、6个7. 若一个正数的两个平方根分别是 和 ,则a的值为( )A、-2 B、2 C、1 D、48. 已知 ,则 ( )A、 B、25 C、32 D、9. 对于正比例函数 , 随 的增大而增大,则 的取值范围( )A、 B、 C、 D、10. 如图的坐标平面上有四直线L1、L2、L3、L4.若这四直线中,有一直线为方程式3x﹣5y+15=0的图形,则此直线为何?( )
A、 +1 B、 -1 C、 D、1-6. 下列各式是二次根式的个数有 ; ; ; ( ); ; ( )A、3个 B、4个 C、5个 D、6个7. 若一个正数的两个平方根分别是 和 ,则a的值为( )A、-2 B、2 C、1 D、48. 已知 ,则 ( )A、 B、25 C、32 D、9. 对于正比例函数 , 随 的增大而增大,则 的取值范围( )A、 B、 C、 D、10. 如图的坐标平面上有四直线L1、L2、L3、L4.若这四直线中,有一直线为方程式3x﹣5y+15=0的图形,则此直线为何?( )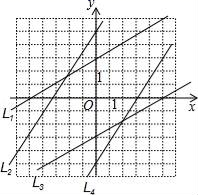 A、L1 B、L2 C、L3 D、L4
A、L1 B、L2 C、L3 D、L4二、填空题
-
11. 如果 , 满足 ,那么 .12. 已知点A(m-1,3)与点B(2,n+1)关于x轴对称,则m-n= .13. 若正比例函数 的图象经过点 ,则 的值是.
三、解答题
-
14. 化简(1)、(2)、15. 解方程(1)、(2)、16. 如图,在四边形ABCD中,AC⊥DC, ADC的面积为30cm2 , DC=12 cm, AB=3 cm, BC=4 cm, 求△ABC的面积.
 17. 如图所示
17. 如图所示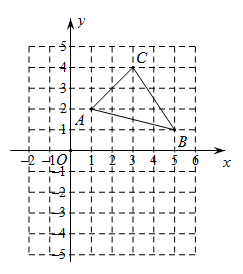 (1)、写出 三个顶点的坐标.(2)、作出 关于 轴对称的 ,并写出 三个顶点的坐标.18. 如图, 平分 , 平分 .试确定 和 的数量关系.
(1)、写出 三个顶点的坐标.(2)、作出 关于 轴对称的 ,并写出 三个顶点的坐标.18. 如图, 平分 , 平分 .试确定 和 的数量关系. 19. 已知一次函数的图象过点 ,且与两坐标轴围成的三角形的面积为2,求此一次函数的表达式.20. 物理兴趣小组 位同学在实验操作中的得分情况如下表:
19. 已知一次函数的图象过点 ,且与两坐标轴围成的三角形的面积为2,求此一次函数的表达式.20. 物理兴趣小组 位同学在实验操作中的得分情况如下表:得分(分)
人数(人)
问:
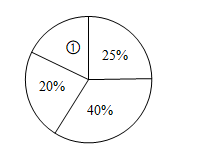
(1)、这 位同学实验操作得分的众数是 , 中位数是(2)、这 位同学实验操作得分的平均分是多少?(3)、将此次操作得分按人数制成如图所示的扇形统计图.扇形①的圆心角度数是多少?