陕西省安康市紫阳县2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-16 类型:期末考试
一、单选题
-
1. 下列各式中,是分式的是( )A、 B、 C、 D、2. 在下列各图形中,分别画出了△ABC中BC边上的高AD,其中正确的是( )A、
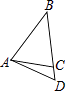 B、
B、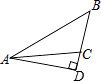 C、
C、 D、
D、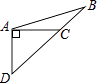 3. 下列图形中,不是轴对称图形的是( )A、
3. 下列图形中,不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 下列分解因式正确的是( )A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 已知 ,则 的值为( )A、 B、 C、 D、7. 如图,在 中,点 在 上,沿 将 对折,点 与点 重合,则图中全等的三角形有( )
4. 下列分解因式正确的是( )A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 已知 ,则 的值为( )A、 B、 C、 D、7. 如图,在 中,点 在 上,沿 将 对折,点 与点 重合,则图中全等的三角形有( ) A、 对 B、 对 C、 对 D、 对8. 已知 是分式方程 的解,则 的值为( )A、 B、 C、 D、9. 如图,在 中, 垂直平分 交 于点 交 于点 .若 ,则 的周长是( )
A、 对 B、 对 C、 对 D、 对8. 已知 是分式方程 的解,则 的值为( )A、 B、 C、 D、9. 如图,在 中, 垂直平分 交 于点 交 于点 .若 ,则 的周长是( ) A、 B、 C、 D、10. 如图,在等腰 中, 点 为 的中点,且 .若 ,则 的长为( )
A、 B、 C、 D、10. 如图,在等腰 中, 点 为 的中点,且 .若 ,则 的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如果一个多边形的每个外角都等于 ,那么这个多边形的内角和是度.12. 计算: .13. 如图,若 ,则 .
 14. 如图,在 中, 平分 点 分别是 上的动点.若 则 的最小值是.
14. 如图,在 中, 平分 点 分别是 上的动点.若 则 的最小值是.
三、解答题
-
15. 分解因式:(1)、(2)、16. 化简:17. 如图,在直角 中, 请用尺规作图法在 上求作一点 使得点 到边 的距离相等.(保留作图痕迹,不写作法)
 18. 在 中,已知 ,若第三边 的长为偶数,求 的周长.19. 解方程: .20. 先化简,再求值: ,其中 .21. 如图,在平面直角坐标系中,每个小方格的边长为 的三个顶点分别为 .请在坐标系中标出 三点,画出 ,并画出 关于y轴对称的图形 ,写出点 的坐标.
18. 在 中,已知 ,若第三边 的长为偶数,求 的周长.19. 解方程: .20. 先化简,再求值: ,其中 .21. 如图,在平面直角坐标系中,每个小方格的边长为 的三个顶点分别为 .请在坐标系中标出 三点,画出 ,并画出 关于y轴对称的图形 ,写出点 的坐标.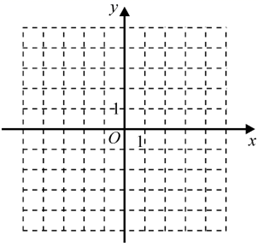 22. 如图,在 中, 点 在 上,过点 作 于点 点 是 边上一点,连接 .若 ,求证: 平分 .
22. 如图,在 中, 点 在 上,过点 作 于点 点 是 边上一点,连接 .若 ,求证: 平分 . 23. 如图,在 中, 平分 交 于点 过点 作 交 的延长线于点 .
23. 如图,在 中, 平分 交 于点 过点 作 交 的延长线于点 . (1)、求 的度数﹔(2)、求证: 是等腰三角形.24. 数学活动课上,张老师准备了若干个如图 的三种纸片, 种纸片是边长为 的正方形, 种纸片是边长为 的正方形, 种纸片是长为 宽为 的长方形,并用 种纸片一张, 种纸片一张, 种纸片两张拼成如图 的大正方形.
(1)、求 的度数﹔(2)、求证: 是等腰三角形.24. 数学活动课上,张老师准备了若干个如图 的三种纸片, 种纸片是边长为 的正方形, 种纸片是边长为 的正方形, 种纸片是长为 宽为 的长方形,并用 种纸片一张, 种纸片一张, 种纸片两张拼成如图 的大正方形. (1)、观察图 ,请你写出代数式 之间的等量关系是;
(1)、观察图 ,请你写出代数式 之间的等量关系是; (2)、根据(1)中的等量关系,解决下列问题;
(2)、根据(1)中的等量关系,解决下列问题;已知 ,求 的值;
已知 ,求 的值.
25. (阅读材科)小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的项角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小明发现若∠BAC=∠DAE,AB=AC,AD=AE,则△ABD≌△ACE.
 (1)、(材料理解)在图1中证明小明的发现.(2)、(深入探究)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:①BD=EC;②∠BOC=60°;③∠AOE=60°;④EO=CO,其中正确的有.(将所有正确的序号填在横线上).(3)、(延伸应用)如图3,AB=BC,∠ABC=∠BDC=60°,试探究∠A与∠C的数量关系.
(1)、(材料理解)在图1中证明小明的发现.(2)、(深入探究)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:①BD=EC;②∠BOC=60°;③∠AOE=60°;④EO=CO,其中正确的有.(将所有正确的序号填在横线上).(3)、(延伸应用)如图3,AB=BC,∠ABC=∠BDC=60°,试探究∠A与∠C的数量关系.