宁夏回族自治区石嘴山市平罗县2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-16 类型:期末考试
一、单选题
-
1. 在 中,若 都是锐角,则 是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、以上都有可能2. 如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=30°,∠2=70°,则∠3等于( )
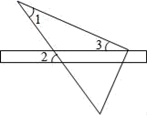 A、40° B、30° C、20° D、15°3. 已知一个正方形的边长为a,将该正方形的边长增加1,则得到的新正方形的面积为( )A、a2+2a+1 B、a2-2a+1 C、a2+1 D、a-14. 已知如图,AB=AE,只需再加一个条件就能证明△ABC≌△AED,下列选项是所加条件,请判断哪一个不能判断△ABC≌△AED( )
A、40° B、30° C、20° D、15°3. 已知一个正方形的边长为a,将该正方形的边长增加1,则得到的新正方形的面积为( )A、a2+2a+1 B、a2-2a+1 C、a2+1 D、a-14. 已知如图,AB=AE,只需再加一个条件就能证明△ABC≌△AED,下列选项是所加条件,请判断哪一个不能判断△ABC≌△AED( )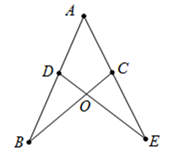 A、∠B=∠E B、AC=AD C、∠ADE=∠ACB D、BC=DE5. 下列各式中,能用平方差公式计算的是( )A、 B、 C、 D、6. 如果把分式 中的 都扩大2倍,那么分式的值( )A、不变 B、缩小2倍 C、扩大2倍 D、无法确定7. 如图,已知AD是△ABC的边BC上的中线,CE是△ADC的边AD上的中线,若△ABD的面积为16cm2 , 则△CDE的面积为( )
A、∠B=∠E B、AC=AD C、∠ADE=∠ACB D、BC=DE5. 下列各式中,能用平方差公式计算的是( )A、 B、 C、 D、6. 如果把分式 中的 都扩大2倍,那么分式的值( )A、不变 B、缩小2倍 C、扩大2倍 D、无法确定7. 如图,已知AD是△ABC的边BC上的中线,CE是△ADC的边AD上的中线,若△ABD的面积为16cm2 , 则△CDE的面积为( ) A、32 cm2 B、16cm2 C、8cm2 D、4cm28. 对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如利用图1可以得到 ,那么利用图2所得到的数学等式是( )
A、32 cm2 B、16cm2 C、8cm2 D、4cm28. 对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如利用图1可以得到 ,那么利用图2所得到的数学等式是( )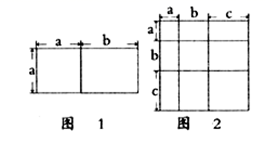 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 计算: .10. 如果一个多边形的内角和与它的外角和相等,那么这个多边形是边形11. 点M(a,5)与点N(-3,b)关于Y轴对称,则a + b =.12. 若 ,则 .13. 如图,在 中,点 是 上的点, ,将 沿着 翻折得到 ,则 °.
 14. 一项工程,甲乙合作b天能完成,甲单独做需要a天完成,则乙独做需天完成.15. 把分式方程 化成整式方程,去分母后的方程为16. 如图,在 中, ,以顶点 为圆心,适当长为半径画弧,分别交 , 于点 , ,再分别以 , 为圆心,大于 的长为半径画弧,两弧交于点 ,作射线 交边 于点 ,若 , 的面积是 ,则 的长为
14. 一项工程,甲乙合作b天能完成,甲单独做需要a天完成,则乙独做需天完成.15. 把分式方程 化成整式方程,去分母后的方程为16. 如图,在 中, ,以顶点 为圆心,适当长为半径画弧,分别交 , 于点 , ,再分别以 , 为圆心,大于 的长为半径画弧,两弧交于点 ,作射线 交边 于点 ,若 , 的面积是 ,则 的长为
三、解答题
-
17. 计算:18. 分解因式:19. 解方程:20. 化简: .21. 如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=50°,求∠EAD的度数.
 22. 如图,轮船从A港出发,以28海里/小时的速度向正北方向航行,此时测的灯塔M在北偏东30°的方向上.半小时后,轮船到达B处,此时测得灯塔M在北偏东60°的方向上.
22. 如图,轮船从A港出发,以28海里/小时的速度向正北方向航行,此时测的灯塔M在北偏东30°的方向上.半小时后,轮船到达B处,此时测得灯塔M在北偏东60°的方向上. (1)、求轮船在B处时与灯塔M的距离;(2)、轮船从B处继续沿正北方向航行,又经半小时后到达C处.求:此时轮船与灯塔M的距离是多少?灯塔M在轮船的什么方向上?23. 如图所示, 在正方形网格中,若点 的坐标为( , ),点 的坐标为(1,1)按要求回答下列问题:
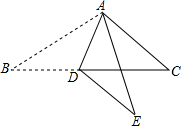
(1)、求轮船在B处时与灯塔M的距离;(2)、轮船从B处继续沿正北方向航行,又经半小时后到达C处.求:此时轮船与灯塔M的距离是多少?灯塔M在轮船的什么方向上?23. 如图所示, 在正方形网格中,若点 的坐标为( , ),点 的坐标为(1,1)按要求回答下列问题: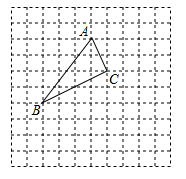 (1)、在图中建立正确的平面直角坐标系;(2)、根据所建立的坐标系,写出点 的坐标;(3)、作出 关于 轴的对称图形 .24. 如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)、在图中建立正确的平面直角坐标系;(2)、根据所建立的坐标系,写出点 的坐标;(3)、作出 关于 轴的对称图形 .24. 如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD. (1)、求证:△BCE≌△DCF;(2)、求证:AB+AD=2AE.25. 为全面打赢脱贫攻坚战,顺利完成古蔺县2019年脱贫摘帽任务,我县某乡镇决定对辖区内一段公路进行改造,根据脱贫攻坚时间安排,需在28天内完成该段公路改造任务.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作只需10天完成.(1)、甲、乙两个工程队单独完成此项工程各需多少天?(2)、若甲工程队每天的工程费用是4.5万元,乙工程队每天的工程费用是2.5万元,请你设计一种方案,既能按时完工,又能使工程费用最少.26. 在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)、求证:△BCE≌△DCF;(2)、求证:AB+AD=2AE.25. 为全面打赢脱贫攻坚战,顺利完成古蔺县2019年脱贫摘帽任务,我县某乡镇决定对辖区内一段公路进行改造,根据脱贫攻坚时间安排,需在28天内完成该段公路改造任务.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作只需10天完成.(1)、甲、乙两个工程队单独完成此项工程各需多少天?(2)、若甲工程队每天的工程费用是4.5万元,乙工程队每天的工程费用是2.5万元,请你设计一种方案,既能按时完工,又能使工程费用最少.26. 在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE. (1)、如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=度;(2)、设 , .
(1)、如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=度;(2)、设 , .①如图2,当点D在线段BC上移动,则 , 之间有怎样的数量关系?请说明理由;
②当点D在直线BC上(线段BC之外)移动,则 , 之间有怎样的数量关系?请直接写出你的结论.