专题24《组合体体积算法》2020-2021学年小升初数学真题汇编专项复习（全国通用）
试卷更新日期：2021-03-16 类型：二轮复习
一、选择题
-
1. 下面4个物体都是由同样大的正方体摆成的。体积最大的是（ ）。A、
B、
C、
D、
2. 一个长方体挖掉一个小正方体（如下图），下面说法正确的是（ ）。
A、体积减少，表面积减少 B、体积减少，表面积增加 C、体积减少，表面积不变 D、体积不变，表面积不变3. 下面四个物体中，体积相等的两个物体是（ ）。
A、①和③ B、②和④ C、③和④ D、①和②二、填空题
-
4. 如图所示，它是由棱长为2cm的正方体堆砌而成的，它的体积是立方厘米，表面积是平方厘米。
5. 如图，三个直立于水平面上的形状完全相同的几何体，将它们拼成如图所示的新几何体，则该新几何体的体积为（结果保留 ）.
6. （如下图)5个棱长2分米的正方体硬纸箱堆放在墙角，体积一共是立方分米，露在外面的硬纸面积是平方分米。
7. 用棱长是1分米的小正方体搭成一个模型，从正面看是
，从上面看是 ，从侧面看是 ，这个模型的体积至少是立方分米。 8. 如图，陀螺的上面是圆柱，下面是圆锥.经过测试，当圆锥的高是圆柱高的75%时，陀螺才能旋转得又稳又快。照着这个标准做了一个陀螺，其中圆柱的底面直径是6厘米，高是6厘米。这个陀螺的体积是立方厘米。
9. 一个机器零件（如图），圆柱部分和圆锥部分的体积之比是。如果圆柱部分的体积是48cm3 ， 这个零件的体积是 cm3。
10. 下图是一个用棱长为1厘米的小正方体拼搭成的立体图形，如果要在此基础上拼搭成一个长方体，这个长方体的体积至少是立方厘米，还需用个这样的小正方体。
11. 小明用几个1立方厘米的正方体摆了一个物体，下面是从不同方向看到的图形。这个物体的表面积是平方厘米，体积是立方厘米。
12. 下图是用棱长1厘米的小正方体拼成的，下图中物体表面积是平方厘米，体积是立方厘米。至少再加个小正方体，就变成一大的正方体。
13. 下图中，甲的表面积与乙的表面积相比较，；甲的体积和乙的体积相比较，。
A、甲大 B、乙大 C、 一样大 D、无法确定
三、计算题
-
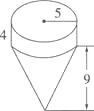
14. 计算下面图形的体积。(单位：cm)
15. 计算下列各图的体积.（单位：厘米）
16. 求下面图形的表面积和体积。
17. 计算立体图形的体积。（单位：dm）
18.(1)、求下图的表面积。（单位：cm）
(2)、求下图的体积。（单位：cm）
19. 如图是由棱长为1cm的小正方体摆成的，它的体积是多少？表面积是多少？
20. 求下列立体图形的体积。(单位：cm)(1)、
(2)、
四、解答题
-
21. 一种健身器材陀螺（如下图），上面是圆柱体，下面是圆锥体。经过测试，当圆柱直径4厘米，高6厘米，圆锥的高是圆柱高的 时，旋转得又快又稳，求这个陀螺的体积有多大？
22. 经过测试，要使一个陀螺旋转起来又稳又快，要满足？下列条件：圆柱直径6厘米，高8厘米，圆锥的高是圆柱高的 。算一算，这时这个陀螺的体积是多大？
23. 一种儿童玩具——陀螺（如图），上面是圆柱，下面是圆锥。经过测试，只有当圆柱底面直径为4厘米，高为5厘米，圆锥的高与圆柱的高的比是3：5时，才能旋转得又稳又快，试问这个陀螺的体积是多大？（保留整立方厘米）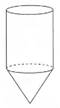
24. 蒙古包也称“毡包”，是蒙古族传统民居，下图中的蒙古包是由一个近似圆柱体和一个近似圆锥体组成的。（单位：米）
(1)、这个蒙古包占地多少平方米？(2)、这个蒙古包内部的空间约是多少立方米？
