专题07《探索规律》2020-2021学年小升初数学真题汇编专项复习(全国通用)
试卷更新日期:2021-03-16 类型:二轮复习
一、单选题
-
1. 按1、 、 、 中的规律,接下来应填( )A、 B、 C、2. 某餐厅里,一张桌子可坐6人,如图所示:

按照上面的规律,n张桌子能坐( )人。
A、6n+4 B、4n+4 C、4n+2 D、6n+63. ,···,请问 是这组数的第( )个数。A、12 B、13 C、14 D、174. 下图是按一定规律连续拼摆制作的图案,按此规律N处的图案应是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 笑笑在某月的日历卡上按照下图的方式圈出了三组数(如图所示),他发现每组数中的四个数都有相同的关系,而且用同样的方法再任意圈出四个数,他们的关系不变。下面的四个表达式中,最能表示每组四个数之间的关系的是( )
5. 笑笑在某月的日历卡上按照下图的方式圈出了三组数(如图所示),他发现每组数中的四个数都有相同的关系,而且用同样的方法再任意圈出四个数,他们的关系不变。下面的四个表达式中,最能表示每组四个数之间的关系的是( ) A、
A、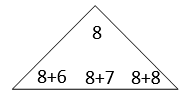 B、
B、 C、
C、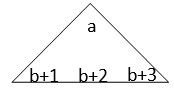 D、
D、 6. 已知○、△、□各代表一个数,根据○+△=52,△+□=46,△-□=28,可知下列选项正确的是( )。A、△=37 B、□=15 C、○=97. 填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m的值是( )。
6. 已知○、△、□各代表一个数,根据○+△=52,△+□=46,△-□=28,可知下列选项正确的是( )。A、△=37 B、□=15 C、○=97. 填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m的值是( )。 A、38 B、52 C、66 D、748. 如下图,用火柴棒搭房子,搭三间用了13根。照这样计算,搭504间用( )根火柴棒。
A、38 B、52 C、66 D、748. 如下图,用火柴棒搭房子,搭三间用了13根。照这样计算,搭504间用( )根火柴棒。 A、2013 B、2015 C、20179. 一列数1,2,2,3,3,3,4,4,4,4,…中的第35个数为( )。A、6 B、7 C、8
A、2013 B、2015 C、20179. 一列数1,2,2,3,3,3,4,4,4,4,…中的第35个数为( )。A、6 B、7 C、8二、填空题
-
10. 按规律填数。
1、3、5、7、9、、13、15。11. 从左到右填数.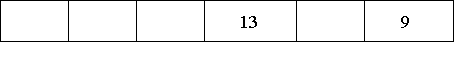 12. 找规律填数:2.6,2.9,3.2, , , 4.1。13. 一列分数的前5个是 、 、 、 、 .根据这5个分数的规律可知,第6个分数是 .14. 右图是一组有规律的图案,第1个图案是由4个基本图形组成,第2个图案是由7个基本图形组成,……则第5个图案是由个基本图形组成。
12. 找规律填数:2.6,2.9,3.2, , , 4.1。13. 一列分数的前5个是 、 、 、 、 .根据这5个分数的规律可知,第6个分数是 .14. 右图是一组有规律的图案,第1个图案是由4个基本图形组成,第2个图案是由7个基本图形组成,……则第5个图案是由个基本图形组成。 15. 如下图所示,4张桌子可坐人,摆n张桌子可以坐人。
15. 如下图所示,4张桌子可坐人,摆n张桌子可以坐人。 16. 摆一摆,找规律。
16. 摆一摆,找规律。
摆第7个图形需要根小棒,摆第n个图形需要根小棒。
17. 1+3==2 1+3+5==21+3+5+7==2 1+3+5+7+…+97+99==2
18. 找规律填数:3, 5, 9,17, 33,。19. 观察下图,每个图形中间是白色小正方形,周围是灰色小正方形。
照这样画下去,第10个图形中有个白色小正方形,个灰色小正方形。
20. 按规律填数:1,8,27, , 125……三、解答题
-
21. 农夫将苹果树种在正方形果园里。为了保护苹果树不被风吹,他在苹果树的周围种了一些针叶树。在下图中,你可以看到农夫种植苹果树的列数n和苹果树数量及针叶树数量的规律。
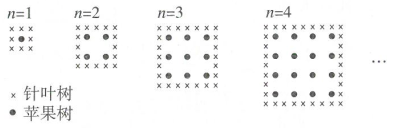 (1)、请你分别用含有n的式子表示苹果树和针叶树的数量。(2)、当农夫种的苹果树列数为多少时,苹果树的数量会等于针叶树的数量?22. 将自然数1~100排列如下表:在这个表里用长方形框出的二行六个数(图中长方形框仅为示意),如果框起来的六个数的和为429,问这六个数中最小的数是几?(用方程解)
(1)、请你分别用含有n的式子表示苹果树和针叶树的数量。(2)、当农夫种的苹果树列数为多少时,苹果树的数量会等于针叶树的数量?22. 将自然数1~100排列如下表:在这个表里用长方形框出的二行六个数(图中长方形框仅为示意),如果框起来的六个数的和为429,问这六个数中最小的数是几?(用方程解) 23. 观察下面点图与算式的关系,找到规律后,解答问题。
23. 观察下面点图与算式的关系,找到规律后,解答问题。 (1)、按点增加的规律给第⑤个图补画上9个点,并在括号里写出点的总数。(2)、请根据上面图中点的总数的变化规律,写出第
(1)、按点增加的规律给第⑤个图补画上9个点,并在括号里写出点的总数。(2)、请根据上面图中点的总数的变化规律,写出第 个图中一共有个点。(用含有n的式子表示)
个图中一共有个点。(用含有n的式子表示) 四、综合题
-
24. 找规律填数。(1)、 , , , , , , ……,这列数的每一项越来越小,越来越接近。(2)、2,3,5,8,12,17, , 。25. 观察下面等式:
第1个等式:(120×120)-(119×121)=1,
第2个等式:(120×120)-(118×122)=4,
第3个等式:(120×120)-(117×123)=9,
第4个等式:(120×120)-(116×124)=16,
……
按照以上规律,解决下列问题:
(1)、写出第5个等式:;(2)、填空:(×)-(×)=144。
