专题07《探索规律》2020-2021学年小升初数学专项复习（江苏省专用）
试卷更新日期：2021-03-16 类型：二轮复习
一、单选题
-
1. 古希腊著名的毕达哥拉期学派把1，3，6，10，…这样的数称为“三角形数”，而把1，4，9， 16，…这样的数称为“正方形数”。从图中可以发现：任何一个大于1的“正方形数”都可以 看作两个相邻的“三角形数”之和。把“正方形数”36写成两个相邻的“三角形数”之和，正确的是（ ）。
A、36=10+26 B、36=15+21 C、36=16+202. 用同样长的小棒摆正方形（每条边用一根小棒），照这样摆，摆6个正方形一共需要（ ）根小棒。
A、19 B、20 C、21 D、223. 将一些小圆球如下图摆放，第六幅图有（ ）个小圆球。
A、30 B、42 C、48 D、564. 瑞士的一位中学教师巴尔末成功地从光谱数据 、 、 、 ……中发现了一个规律，从而打开了光谱奥妙的大门。请你根据这个规律写出第5个数是（ ）。A、 B、 C、 D、5. 按如图规律摆放三角形则第⑥个图三角形的个数为（ ）。
A、15 B、17 C、20 D、246. 将正方形图①作如下操作：第1次，分别连接对边中点如图②，得到5个正方形（1个正方形加上4个中等正方形）；第2次，将图②左上角正方形按上述方法再分割如图③，得到9个正方形；像这样操作8次，可以得到（ ）个正方形。
A、29 B、32 C、33二、填空题
-
7. 下图中，毎个黑色的圆片周围都摆有6个白色圆片。
照这样摆下去，10个黑色圆片周围一共摆有个白色圆片；n个黑色圆片周围一共摆有个白色圆片。
8. 刘松在一组数3、4、6，10……里发现了规律，他把这个规律写成一个等式：前面的数×a-a=下一个数。在这个等式里，a代表的是同一个数。那么，这里的a代表的数是 ， 按照这样的规律，第6个数是。9. 如图是某同学在沙滩上用石子摆成的小房子：照这样摆下去，第6个小房子用了块石子；第n个小房子用了块石子。
10. 按照下面图形与数的排列规律，下一个数应是 ， 第n个数是 ．
11. 按下面图形排列的规律，第10幅图有个正方形。
12. 如图，它是由火柴棒拼成的图案，如果在这个图案中用了51根火柴棒，可拼成个三角形．
13. 如图，若每个小正方体的棱长都是1厘米，则第2个图形的表面积是平方厘米，第n个图形一共需要个小正方体搭成。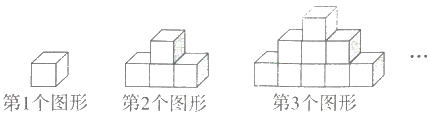
14. 下图中图①是一个三角形，分别连接这个三角形三边的中点得到图②，再分别连接图②中间的小三角形三边的中点得图③，按这样的方法继续下去，第⑥个图形有个三角形。
15. （1+3+5+7）－（1+3+5）＝2－ 2＝16. ， ， ……按这组数的规律，第五个数应该是；如果这样一直写下去，那么这个数会越来越接近。17. 学校阅览室有能坐4人的方桌，如果多于4人，就把方桌拼成一行，2张方桌拼成一行能坐6人（如图所示），请你结合这个规律算一算，6张桌子拼成一行能坐人，n张桌子拼成一行能坐人。
三、解答题
-
18. 看图回答
仔细观察上面的点子图，根据每个图中点子的排列规律，想一想，可以怎样计算每个图中点子的总个数？请你把下表填写完整。
序号
1
2
3
4
……
表示点子数的算式
1
1+4
……
点子的总个数
1
……
观察表中数据，如果用A表示第n个图形中点子的个数，A和n之间的关系可以表示成：
A=。
19. 将11至17这七个数字，填入图中的○内，使每条线上的三个数的和相等。
20. 一批砖块，长和宽都是整厘米数，如果全部横着排，可以排1224厘米；如果按一横、一竖……这样的顺序排下去，可以排1024厘米。已知砖块的长比宽多8厘米。
(1)、这些砖共有多少块?(2)、如果用这些砖按二横一竖地排下去（如图）一共可以排多少厘米?21. 下面的每一个图形都是由△、口、O中的两个组成的。观察各个图形，根据图形下面的数找出规律，画出表示“23”和“12”的图形。
22. 图①、②、③、④都是平面图形。
(1)、数一数每个图形各有多少个顶点，多少条边，这些边围出了多少个区城，将结果填入下表中（其中①已填好）。图形
顶点数
边数
区域数
①
4
6
3
②
③
④
(2)、观察上表，推断一个平面图形的顶点数、边数、区域数之间的关系。(3)、现已知某一平面图形有999个顶点和999个区城，试根据（2）中推断出的关系，确定这个图形有多少条边。23. 现有若干个圆环，它的外直径是5厘米，环宽是0.5厘米，将它们（如下图）扣在一起，拉紧后测量其长度，请完成表格。
圆环个数
1
2
3
4
5
6
……
拉紧后的长度/cm
(1)、请完成表格。(2)、根据表中规律，11个圆环拉紧后的长度是多少厘米?(3)、设圆环的个数为a，拉紧后的总长度为S，你能用一个关系式表示你发现的规律吗?(4)、若拉紧后的长度是77厘来，则它是由多少个圆环扣成的?四、综合题
-
24. 小明用吸管和图钉钉三角形形状（如下图，线段表示吸管，黑点表示图钉）。
(1)、照样子钉4个三角形，需要个图钉和个吸管。(2)、小明用100个图钉，同时要再用根吸管，就能钉成个三角形。25. 探索与发现意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1、1、2、3、5、8、13……计算12+12+22+32+52+82+132这样的算式时有简便方法吗？
丁丁遇到这个问题时，想到用“数形结合”的方法来探索，于是他以这组数中各个数作为正方形的边长构造成正方形，再拼成如图所示的长方形来研究．
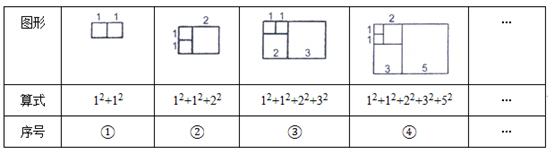(1)、观察上面的图形和算式，你能把下面算式补充完整吗？12+12＝1×2
12+12+22＝2×3
12+12+22+32＝×
12+12+22+32+52＝×
(2)、若按此规律继续拼长方形，则序号为的长方形面积数是714．