河北省邢台市威县2019-2020学年七年级下学期数学月考试卷

试卷更新日期：2021-03-15 类型：月考试卷

进入出卷网下载

一、单选题

1. 在下面四个数中，是无理数的是（）

A、3.1415 B、 $\sqrt{2}$ C、 $\frac{22}{7}$ D、 $\sqrt[3]{8}$

查看试题解析
2. 如图，笑脸所在的象限的是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. “ $\frac{16}{25}$ 的算术平方根是 $\frac{4}{5}$ ”，用式子表示为（）

A、± $\sqrt{\frac{16}{25}}$ ＝± $\frac{4}{5}$ B、 $\sqrt{\frac{16}{25}}$ ＝± $\frac{4}{5}$ C、 $\sqrt{\frac{16}{25}}$ ＝ $\frac{4}{5}$ D、± $\sqrt{\frac{16}{25}}$ ＝ $\frac{4}{5}$

查看试题解析
4. 如图，把河AB中的水引到C，拟修水渠中最短的是（）

A、CM B、CN C、CP D、CQ

查看试题解析
5. 下列不是方程 $2 x + y = 10$ 的解的是（）

A、 ${\begin{array}{l} x = 2 \\ y = 6 \end{array}$ B、 ${\begin{array}{l} x = - 2 \\ y = 14 \end{array}$ C、 ${\begin{array}{l} x = 3 \\ y = 6 \end{array}$ D、 ${\begin{array}{l} x = - 3 \\ y = 16 \end{array}$

查看试题解析
6. 下列有污迹的电影票中能让小华准确找到座位的是（）

A、 B、 C、 D、

查看试题解析
7. 如果 $a / / b$ ， $b / / c$ ，那么 $a / / c$ ，这个推理的依据是 $($ $)$

A、等量代换 B、两直线平行，同位角相等 C、平行公理 D、平行于同一直线的两条直线平行

查看试题解析
8.
点A的位置如图所示，则关于点A的位置下列说法中正确的是（　　）

A、距点O4km处 B、北偏东40°方向上4km处 C、在点O北偏东50°方向上4km处 D、在点O北偏东40°方向上4km处

查看试题解析
9. 与 $2 + \sqrt{5}$ 最接近的整数是（）

A、2 B、3 C、4 D、5

查看试题解析
10. 下列可以说明命题“若 $a^{2} > 1$ ，则 $a > 1$ ”是假命题的反例是（）

A、 $a = 2$ B、 $a = 0$ C、 $a = - 2$ D、 $a = - \frac{1}{2}$

查看试题解析
11. “鸡兔同笼”是我国民间流传的诗歌形式的数学题：“鸡兔同笼不知数，三十六头笼中露，看来脚有100只，几多鸡儿几多兔”解决此问题，设鸡为x只，兔为y只，则所列方程组正确的是（）

A、 ${\begin{cases} \end{cases} \begin{array}{l} x + y = 36 \\ x + 2 y = 100 \end{array}$ B、 ${\begin{cases} \end{cases} \begin{array}{l} x + y = 36 \\ 4 x + 2 y = 100 \end{array}$ C、 ${\begin{cases} \end{cases} \begin{array}{l} x + y = 36 \\ 2 x + 4 y = 100 \end{array}$ D、 ${\begin{cases} \end{cases} \begin{array}{l} x + y = 36 \\ 2 x + 2 y = 100 \end{array}$

查看试题解析
12. 在平面直角坐标系中，点A'（2，﹣3）可以由点A（﹣2，3）通过两次平移得到，正确的是（）

A、先向左平移4个单位长度，再向上平移6个单位长度 B、先向右平移4个单位长度，再向上平移6个单位长度 C、先向左平移4个单位长度，再向下平移6个单位长度 D、先向右平移4个单位长度，再向下平移6个单位长度

查看试题解析
13. 已知x，y满足 ${\begin{array}{l} 2 x - 3 y = 1 ① \\ 3 x - 2 y = 5 ② \end{array}$ ，如果①×a+②×b可整体得到x+11y的值，那么a，b的值可以是（）

A、 $a = 2$ ， $b = - 1$ B、 $a = - 4$ ， $b = 3$ C、 $a = 1$ ， $b = - 7$ D、 $a = - 7$ ， $b = 5$

查看试题解析
14. 对于非零的两个实数 $m ， n$ ，定义一种新运算，规定 $m * n = a m - b n$ ，若 $2 * (- 3) = 8$ ， $5 * 3 = - 1$ ，则 $(- 3) * (- 2)$ 的值为（）

A、 $1$ B、 $- 1$ C、 $- 6$ D、 $6$

查看试题解析

二、填空题

15. 计算： $\sqrt[3]{- 0.001}$ ＝．

查看试题解析
16. 为了测量一座古塔外墙底部的底角∠AOB的度数，李潇同学设计了如下测量方案：作AO，BO的延长线OD，OC，量出∠COD的度数，从而得到∠AOB的度数．这个测量方案的依据是．

查看试题解析
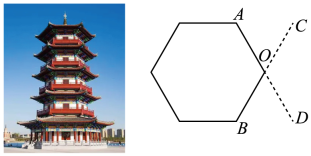17. 如图，将面积为3的正方形放在数轴上，以表示实数1的点为圆心，正方形的边长为半径，作圆交数轴于点 $A$ 、 $B$ ．①线段 $A B =$ ；②点 $A$ 表示的数为．

查看试题解析

三、解答题

18. 如图，经过平移，△ABC的边AB移到了EF，作出平移后的三角形．

查看试题解析
19. 解方程组： ${\begin{array}{l} x + y = 11 ① \\ 2 x - y = 7 ② \end{array}$ ．

(1)、小组合作时，发现有同学这么做：①+②得 $3 x = 18$ ，解得 $x = 6$ ，代入①得 $y = 5$ ．
∴这个方程组的解是 ${\begin{array}{l} x = 6 \\ y = 5 \end{array}$ ，该同学解这个方程组的过程中使用了消元法，目的是把二元一次方程组转化为．

(2)、请你用另一种方法解这个方程组．

查看试题解析
20. 如图，图中显示了10名同学平均每周用于阅读课外书的时间和用于看电视的时间（单位： $h$ ）

(1)、用有序实数对表示图中各点；

(2)、平均每周用于阅读课外书的时间和用于看电视的时间的总共 $10h$ 的同学有多少名？

(3)、如果设平均每周用于阅读课外书的时间超过用于看电视的时间的同学为 $a$ 名，设平均每周用于阅读课外书的时间少于用于看电视的时间的同学为 $b$ 名，求 $b - a$ 的值．

查看试题解析
21. 已知平面直角坐标系中有一点 $M (m - 1 ， 2 m + 3)$

(1)、点 $M$ 在 $x$ 轴上，求 $M$ 的坐标；

(2)、点 $N (5 ， - 1)$ 且 $M N // x$ 轴时，求 $M$ 的坐标；

(3)、点 $M$ 到 $y$ 轴的距离为2，求 $M$ 的坐标．

查看试题解析
22. 小辰想用一块面积为100cm²的正方形纸片，沿着边的方向裁出一块面积为90cm²的长方形纸片，使它的长宽之比为5：3．小辰能否用这张正方形纸片裁出符合要求的纸片？若能请写出具体栽法；若不能，请说明理由．

查看试题解析
23. 已知，如图， $C D ⊥ A B ， E F ⊥ A B$ ，垂足分别为 $D 、 F ， ∠ B + ∠ B D G = 180 °$ ，试说明 $∠ B E F = ∠ C D G$ .

查看试题解析
24. 如图，某工厂与A、B两地有公路、铁路相连．这家工厂从A地购买一批每吨2000元的原料运回工厂，制成每吨7500元的产品运到B地．已知公路运价为2元/ （吨·千米），铁路运价为 1.5元/（吨·千米），且这两次运输共支出公路运输费2.6万元，铁路运输费15.6万元。

求：

(1)、该工厂从A地购买了多少吨原料？制成运往B地的产品多少吨？

(2)、若不计人力成本，这批产品盈利多少元？（盈利=销售款-原料费-运输费）

查看试题解析