河北省石家庄市高邑县2019-2020学年八年级下学期数学月考试卷

试卷更新日期：2021-03-15 类型：月考试卷

进入 出卷网 下载

一、单选题

  • 1. 下列调查中，①调查本班同学的视力；②调查一批节能灯管的使用寿命；③为保证“神舟九号”的成功发射，对其零部件进行检查；④对乘坐某班次客车的乘客进行安检．其中适合采用抽样调查的是（ ）
    A、① B、② C、③ D、④

    查看试题解析

  • 2. 在函数 y=x−3 中，自变量 x 的取值范围是（     ）
    A、x<3 B、x>3 C、x≥3 D、x≤3

    查看试题解析

  • 3. 今年我市有近4万名考生参加中考，为了解这些考生的数学成绩，从中抽取1000名考生的数学成绩进行统计解析，以下说法正确的是（）

    A、这1000名考生是总体的一个样本 B、近4万名考生是总体 C、每位考生的数学成绩是个体 D、1000名学生是样本容量

    查看试题解析

  • 4. 点P在第四象限，P到x轴的距离为2，到y轴的距离为3，那么点P的坐标为（  ）
    A、（2，﹣3） B、（3，﹣2）        C、（﹣2，3） D、（﹣3，2）

    查看试题解析

  • 5. 若0＜m＜2，则点P（m－2，m）在（   ）
    A、第一象限 B、第二象限 C、第三象限 D、第四象限

    查看试题解析

  • 6. 平行四边形、矩形、菱形、正方形都具有的性质是（　　）

    A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、对角线互相垂直平分且相等

    查看试题解析

  • 7. 若一个正多边形的一个外角是45°，则这个正多边形的边数是（   ）
    A、6 B、8 C、10 D、12

    查看试题解析

  • 8. 若顺次连接四边形ABCD各边的中点所得四边形是菱形，则四边形ABCD一定是（   ）
    A、菱形 B、对角线互相垂直的四边形 C、矩形 D、对角线相等的四边形

    查看试题解析

  • 9. 已知一次函数y=kx-k，若y随x的增大而增大，则图象经过（ ）
    A、第一､二､三象限 B、第一､三､四象限 C、第一､二､四象限 D、第二､三､四象限

    查看试题解析

  • 10. 甲、乙、丙、丁四位同学到木工厂参观时，一木工师傅拿尺子要他们帮忙检测一个窗框是否是矩形，他们各自做了如下检测，检测后，他们都说窗框是矩形，你认为最有说服力的是（    ）
    A、甲量的窗框两组对边分别相等 B、丙量的窗框的一组邻边相等 C、乙量的窗框的对角线相等 D、丁量的窗框的两组对边分别相等且两条对角线也相等

    查看试题解析

  • 11. ▱ ABCD的对角线AC、BD相交于点O，若AB=5，△OCD的周长为16，则AC与BD的和是（   ）
    A、10 B、11 C、12 D、22

    查看试题解析

  • 12. 某航空公司规定，旅客乘机所携带行李的质量x（kg）与其运费y（元）由如图所示的一次函数图象确定，那么旅客可携带的免费行李的最大质量为（     ）


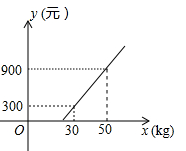    A、20kg B、25kg C、28kg D、30kg

    查看试题解析

  • 13. 如图，E、F分别是正方形ABCD的边CD、AD上的点，且CE=DF，AE、BF相交于点O，下列结论：

    ⑴AE=BF；（2）AE⊥BF；（3）AO=OE；（4） SΔAOB=S四边形DEOF 中正确的有（    ）

    A、4个 B、3个 C、2个 D、1个

    查看试题解析

  • 14. 在物理实验课上，小明用弹簧称将铁块A悬于盛有水的水槽中，然后匀速向上提起，直至铁块完全露出水面一定高度，则下图能反映弹簧称的读数y(单位N)与铁块被提起的高度x(单位cm)之间的函数关系的大致图象是（ ）

    A、 B、 C、 D、

    查看试题解析

  • 15. 若定义： f(a ， b)=(−a ， b) ， g(m ， n)=(m ， −n) ，例如 f(1 ， 2)=(−1 ， 2) ， g(−4 ， −5)=(−4 ， 5) ，则 g(f(2 ， −3)) =（   ）
    A、(2 ， −3) B、(−2 ， 3) C、(2 ， 3) D、(−2 ， −3)

    查看试题解析

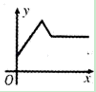  • 16. 我市某储运部紧急调拨一批物资，调进物资共用4小时，调进物资2小时后开始调出物资（调进物资与调出物资的速度均保持不变）.储运部库存物资 S （吨）与时间 t （小时）之间的函数关系如图所示，这批物资从开始调进到全部调出需要的时间是（  ）

    A、4小时 B、4.3小时 C、4.4小时 D、5小时

    查看试题解析

二、填空题

  • 17. 若点 P(a2−9,a−1) 在 y 轴的负半轴上，则点 P 的坐标为

    查看试题解析

  • 18. 如图，▱ABCD绕点A逆时针旋转30°，得到▱AB′C′D′（点B′与点B是对应点，点C′与点C是对应点，点D′与点D是对应点），点B′恰好落在BC边上，则∠C=

    查看试题解析

  • 19. 已知菱形ABCD的两条对角线分别为6和8，M、N分别是边BC、CD的中点，P是对角线BD上一点，则PM+PN的最小值= ．

    查看试题解析

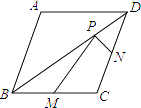  • 20. 如图，已知函数y＝2x＋b与函数y＝kx－3的图象交于点P(4，－6)，则不等式kx－3＞2x＋b的解集是.

    查看试题解析

三、解答题

  • 21. 已知：如图，在▱ABCD中，E、F是对角线BD上的两点，且BE＝DF，

    求证：四边形AECF是平行四边形．

    查看试题解析

  • 22. 某校为了解该校九年级学生对蓝球、乒乓球、羽毛球、足球四种球类运动项目的喜爱情况，对九年级部分学生进行了随机抽样调查，每名学生必须且只能选择最喜爱的一项运动项目，将调查结果统计后绘制成如图两幅不完整的统计图，请根据图中的信息，回答下列问题：

    (1)、这次被抽查的学生有人；请补全条形统计图；
    (2)、在统计图2中，“乒乓球”对应扇形的圆心角是度；
    (3)、若该校九年级共有480名学生，估计该校九年级最喜欢足球的学生约有人．

    查看试题解析

  • 23. 如图，直线y=kx-6经过点A（4，0），直线y=-3x+3与x轴交于点B，且两直线交于点C．

    (1)、求k的值；
    (2)、求△ABC的面积.

    查看试题解析

  • 24. 网络时代的到来，很多家庭都接入了网络，电信局规定了拨号入网两种收费方式，用户可以任选其一：A：计时制：0.05元／分；B：全月制：54元／月（限一部个人住宅电话入网）．此外B种上网方式要加收通信费0.02元／分．
    (1)、某用户某月上网的时间为x小时，两种收费方式的费用分别为 y1 （元）、 y2 （元），写出 y1 、 y2 与x之间的函数关系式．
    (2)、在上网时间相同的条件下，请你帮该用户选择哪种方式上网更省钱？

    查看试题解析

  • 25. 如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．

    (1)、求证：CE=CF；
    (2)、若点G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？

    查看试题解析

  • 26. 甲、乙两工程队维修同一段路面，甲队先清理路面，乙队在甲队清理后铺设路面．乙队在中途停工了一段时间，然后按停工前的工作效率继续工作．在整个工作过程中，甲队清理完的路面长y（米）与时间x（时）的函数图象为线段OA，乙队铺设完的路面长y（米）与时间x（时）的函数图象为折线BC-CD-DE，如图所示，从甲队开始工作时计时．

    (1)、分别求线段BC、DE所在直线对应的函数关系式．
    (2)、当甲队清理完路面时，求乙队铺设完的路面长．

    查看试题解析