山西省大同市2019-2020学年九年级下学期数学第一次月考试卷

试卷更新日期：2021-03-15 类型：月考试卷

进入出卷网下载

一、单选题

1. 计算 $- 5 - 3$ 的结果是（）

A、 $8$ B、 $- 2$ C、 $2$ D、 $- 8$

查看试题解析
2. 下列运算正确的是（）

A、 $2 a^{2} \cdot a^{3} = 2 a^{6}$ B、 $a + a = a^{2}$ C、 ${(2 a)}^{2} = 4 a^{2}$ D、 $a^{6} \div a^{3} = a^{2}$

查看试题解析
3. 近年来，我市认真践行习近平总书记“绿水青山就是金山银山”的生态文明建设理念，坚持规模化推进荒山造林，致力于大林业生态片区建设，取得良好效果.去年，全市共完成营造林任务 $437130$ 亩，实现了由“煤都黑”到“大同蓝”的华丽转身.其中数据“ $437130$ 亩” 可用科学记数法表示为（）

A、 $43.7130 \times 10^{4}$ 亩 B、 $4.37130 \times 10^{5}$ 亩 C、 $4.37130 \times 10^{6}$ 亩 D、 $437.130 \times 10^{3}$ 亩

查看试题解析
4. 用配方法解一元二次方程 $x^{2} - 4 x + 2 = 0$ ，下列配方正确的是（）

A、 ${(x + 2)}^{2} = 2$ B、 ${(x - 2)}^{2} = - 2$ C、 ${(x - 2)}^{2} = 2$ D、 ${(x - 2)}^{2} = 6$

查看试题解析

5. 疫情当前，全国各地企业积极践行社会责任，加急生产防御疫情急需的

84

消毒液.某人统计了本市六天当中消毒液的日产能，情况记录如下：

日期	2月1日	2月2日	2月3日	2月4日	2月5日	2月6日
日产能(吨)	$100$	$95$	$106$	$102$	$120$	$100$

则这6天的日产能的众数和中位数(单位：吨)分别是（）

A、

100, 95

B、

100, 101

C、

102, 100

D、

100, 103

查看试题解析

6. 我国古代秦汉时期有一本数学著作，它在世界数学史上首次正式引入负数及其加减法运算法则，这本著作的名称是（）

A、《海岛算经》 B、《孙子算经》 C、《周髀算经》 D、《九章算术》

查看试题解析
7. 在 $△ A B C$ 中， $∠ C = 90^{\circ} ，$ 将 $△ A B C$ 绕点B逆时针旋转 $90 °$ ，点A旋转后的对应点为 $A'$ ，若 $B C = 3 ， A C = 4$ ，则线段 $A A'$ 的长为（）

A、 $5$ B、 $6$ C、 $5 \sqrt{2}$ D、 $4 \sqrt{2}$

查看试题解析
8. 不等式组 ${\begin{array}{l} \frac{3 x - 1}{2} > 2 - x \\ 8 - 4 x \leq 0 \end{array}$ 的解集在数轴上可表示为（）

A、 B、 C、 D、

查看试题解析
9. 要得到抛物线y＝2（x﹣4）²+1，可以将抛物线y＝2x²（）

A、向左平移4个单位长度，再向上平移1个单位长度 B、向左平移4个单位长度，再向下平移1个单位长度 C、向右平移4个单位长度，再向上平移1个单位长度 D、向右平移4个单位长度，再向下平移1个单位长度

查看试题解析
10. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 ° ， ∠ A = 30 ° ， B C = 4 \sqrt{3}$ ，以直角边 $A C$ 为直径作 $⊙ O$ 交 $A B$ 于点D，则图中阴影部分的面积是（）

A、 $30 \sqrt{3} - 3 π$ B、 $15 \sqrt{3} - 3 π$ C、 $15 \sqrt{3} - 6 π$ D、 $30 \sqrt{3} - 6 π$

查看试题解析

二、填空题

11. 分解因式： $a^{3} - a b^{2}$ =.

查看试题解析
12. 如果一个多边形的内角和等于它的外角和的2倍，那么这个多边形
是边形．

查看试题解析
13. 数形结合是数学解题中常用的思想方法，使用数形结合的方法，很多问题可迎刃而解，且解法简捷．如图所示是一次函数 $y = k x + b$ 在平面直角坐标系中的图象，通过观察图象我们就可以得到方程 $k x + b = 0$ 的解为．

查看试题解析
14. 如图，平面直角坐标系中，点 $A ， B$ 分别在函数 $y = \frac{2}{x} (x > 0)$ 与 $y = - \frac{6}{x} (x < 0)$ 的图象上，点P在x轴上．若 $A B / / x$ 轴，则 $△ P A B$ 的面积为．

查看试题解析
15. 如图，已知在 $△ A B C B C$ 中， $B C$ 边上的高 $A D$ 与 $A C$ 边上的高 $B E$ 交于点 $F ，$ 且 $∠ B A C = 45 ° ， B D = 3 ， C D = 2 ，$ 则 $A D$ 的长为．

查看试题解析

三、解答题

16.

(1)、计算： $- \sqrt{27} - {(\frac{1}{2})}^{- 1} + 6 s i n 60^{\circ} + | 1 - \sqrt{2} |$ ．

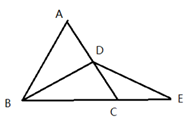
(2)、先化简，再求值： $(2 - \frac{x - 1}{x + 1}) \div \frac{x^{2} + 6 x + 9}{x^{2} - 1}$ 其中 $x = 3$ ．

查看试题解析
17. 如图，三角形ABC是等边三角形，BD是中线，延长BC至E，使CE=CD.求证：DB=DE.

查看试题解析
18. 为发展学生的核心素养，培养学生的综合能力，某学校计划开设四门选修课：乐器、舞蹈、绘画、书法，学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门) .对调查结果进行整理，绘制成如下两幅不完整的统计图，请结合图中所给信息解答下列问题：

(1)、本次调查的学生共有人，在扇形统计图中，m的值是；

(2)、将条形统计图补充完整；

(3)、在被调查的选修书法的学生中，有1名为女同学，其余为男同学，现要从选修书法的同学中随机抽取2名同学代表学校参加某社区组织的书法活动，请你用列表或画树状图的方法.求所抽取的2名同学恰好是1名男同学和1名女同学的概率．

查看试题解析
19. 疫情防控形势下，人们在外出时都应戴上口罩以保护自己免受新型冠状病毒感染.某药店用4000元购进若干包一次性医用口罩，很快售完，该店又用 $7500$ 元钱购进第二批这种口罩，所进的包数比第一批多 $50 %$ ，每包口罩的进价比第一批每包口罩的进价多 $0.5$ 元，请解答下列问题：

(1)、求购进的第一批医用口罩有多少包；

(2)、政府采取措施，在这两批医用口罩的销售中，售价保持了一致.若售完这两批口罩的总利润不高于 $3500$ 元钱，那么药店销售该口罩每包的最高售价是多少元？

查看试题解析
20. 如图， $R t △ A B C$ 中， $∠ A B C = 90^{\circ} ，$ 以 $A B$ 为直径作 $⊙ O$ ，交 $A C$ 于点 $D ，$ 点E是 $A B$ 延长线上的一点，且 $∠ B D E = ∠ A$ ．

(1)、判断 $D E$ 与 $⊙ O$ 的位置关系，并说明理由；

(2)、若 $A B = 6 ， ∠ C = 60 °$ ，求 $D E$ 的长．

查看试题解析
21. 为表达全国各族人民对抗击新冠肺炎疫情斗争牺牲烈士和逝世同胞的深切哀悼，国务院决定，2020年4月4日举行全国性哀悼活动在此期间，全国和驻外使领馆下半旗志哀下半旗时，应当先将国旗升至杆顶，然后降至旗顶与杆顶之间的距离为旗杆全长的三分之一处．如图，将国旗升至杆顶A后，在C点处测得旗顶A的仰角为 $50^{\circ}$ ，再下到旗杆全长处的D点 (即 $A D = \frac{1}{3} A B$ )， $E$ 在 $B C$ 的延长线上且 $C E = 30$ 米，在E处测得旗顶D的仰角为 $10 ° ，$ 求旗杆 $A B$ 的高度． (参考数据： $t a n 50 ° \approx 1.2 ， t a n 10 ° \approx 0.2$ )

查看试题解析
22. 综合与实践
$A 4$ 纸是我们学习工作最常用的纸张之一，其长宽之比是 $\sqrt{2} ： 1$ ，我们定义：长宽之比是 $\sqrt{2} ： 1$ 的矩形纸片称为“标准纸”．

操作判断：

(1)、如图1所示，矩形纸片 $A B C D (A D = \sqrt{2} A B)$ 是一张“标准纸”，将纸片折叠一次，使点B与D重合，再展开，折痕 $E F$ 交 $A D$ 边于点 $E ，$ 交 $B C$ 边于点 $F$ ，若 $A B = 1 ，$ 求 $C F$ 的长，

(2)、如图2，在（1）的基础上，连接 $B D ，$ 折痕 $E F$ 交 $B D$ 于点O，连接 $B E ，$ 判断四边形 $B F D E$ 的形状，并说明理由．

(3)、探究发现：
如图3所示，在(1)和(2)的基础上，展开纸片后，将纸片再折叠一次，使点A与点C重合，再展开，痕 $M N$ 交 $A D$ 边于点M， $B C$ 交边于点 $N ，$ 交 $B D$ 也是点O.然后将四边形 $E N F M$ 剪下，探究纸片 $E N F M$ 是否为“标准纸”，说明理由．

查看试题解析
23. 综合与探究
如图，抛物线 $y = - \frac{1}{2} x^{2} + b x + c$ 与x轴交于 $A ， B$ 两点，与y轴交于点C，且 $O B = O C = 3 ，$ 点D是 $∠ B O C$ 的平分线与抛物线的交点．

(1)、求抛物线的解析式及点D的坐标；

(2)、点E在平面直角坐标系内，且以 $O 、 B 、 D 、 E$ 点为顶点的四边形是平行四边形，请直接写出满足条件的点E的坐标．

(3)、若点P是直线 $B C$ 上方抛物线上的一个动点，且点P的横坐标为 $m ，$ 请写出 $△ B C P$ 的面积S与m之间的关系式，并求出m为何值时， $△ B C P$ 的面积S有最大值，最大值为多少．

查看试题解析