辽宁省锦州市2019-2020学年九年级下学期数学第二次月考试卷
试卷更新日期:2021-03-15 类型:月考试卷
一、单选题
-
1. 下列四个数:-3, , ,-0.5中,相反数最大的数是( )A、-3 B、 C、 D、-0.52. 剪纸艺术是最古老的中国民间艺术之一,作为一种镂空艺术,它能给人以视觉上透空的感觉和艺术享受,下列照片中剪纸图案既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 已知 则下列对m值的范围估算正确的是( )A、 B、 C、 D、4. 如图是由5个大小相同的小立方体搭成的几何体,这个几何体的左视图是( )
3. 已知 则下列对m值的范围估算正确的是( )A、 B、 C、 D、4. 如图是由5个大小相同的小立方体搭成的几何体,这个几何体的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 在一场排球比赛中,某排球队6名场上队员的身高(单位: )是:180,184,188,190,192,194.如果用一名身高为 的队员替换场上身高为 的队员,那么换人后与换人前相比,场上队员身高的平均数和方差大小变化正确的是( )A、平均数变小,方差变小 B、平均数变小,方差变大 C、平均数变大,方差变小 D、平均数变大,方差变大6. 小亮的妈妈到超市购买大米,第一次按原价购买,用了100元,几天后,遇上这种大米按原价降低了 出售,她用120元又购买了一些,两次一共购买了 .设这种大米的原价是每千克x元,则根据题意所列的方程是( )A、 B、 C、 D、7. 如图, 的顶点O在坐标原点上, 边在x轴上, , ,把 绕点A按顺时针方向转到 ,使得点 的坐标是 则在这次旋转过程中线段 扫过部分(阴影部分)的面积为( )
5. 在一场排球比赛中,某排球队6名场上队员的身高(单位: )是:180,184,188,190,192,194.如果用一名身高为 的队员替换场上身高为 的队员,那么换人后与换人前相比,场上队员身高的平均数和方差大小变化正确的是( )A、平均数变小,方差变小 B、平均数变小,方差变大 C、平均数变大,方差变小 D、平均数变大,方差变大6. 小亮的妈妈到超市购买大米,第一次按原价购买,用了100元,几天后,遇上这种大米按原价降低了 出售,她用120元又购买了一些,两次一共购买了 .设这种大米的原价是每千克x元,则根据题意所列的方程是( )A、 B、 C、 D、7. 如图, 的顶点O在坐标原点上, 边在x轴上, , ,把 绕点A按顺时针方向转到 ,使得点 的坐标是 则在这次旋转过程中线段 扫过部分(阴影部分)的面积为( )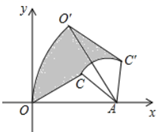 A、 B、 C、 D、8. 如图,正方形 的边长为4.点E,F,G,H分别在边 , , , 上(编点除外),且 .分别将 , , , 沿 , , , 翻折,得到四边形 ,设 , 则y关于x的函数图象大致为( )
A、 B、 C、 D、8. 如图,正方形 的边长为4.点E,F,G,H分别在边 , , , 上(编点除外),且 .分别将 , , , 沿 , , , 翻折,得到四边形 ,设 , 则y关于x的函数图象大致为( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 分解因式: .10. 人民日报2020年2月29日消息,国家卫健委医政医管局监察专员郭燕红表示,目前派出的医疗队总人数已达4.2万人,在对患者医疗救治中发挥了非常重要的作用请将“4.2万”用科学记数法表示为 .11. 2020年3月12日是我国第42个植树节,某林业部门要考察种幼树在一定条件下的移植成活率,幼树移植过程中的一组统计数据如下表:
幼树移植数(棵)
100
2500
4000
8000
20000
30000
幼树移植成活数(棵)
87
2215
3520
7056
17580
26430
幼树移植成活的频率
0.870
0.886
0.880
0.882
0.879
0.881
请根据统计数据,估计这种幼树在此条件下移植成活的概率是 . (结果精确到0.01)
12. 若关于x的一元二次方程 有两个实数根,则a的取值范围是 .13. 如图,五边形 是正五边形,点D在 上,若 , ,则 . 14. 如图,分别以 的斜边 ,直角边 为边向外作等边 和等边 , 为 的中点,分别连接 , , , 与 相交于点G,著 ,下列四个结论:① ;②四边形 为平行四边形;③ ;④ .其中结论正确的是(填序号即可).
14. 如图,分别以 的斜边 ,直角边 为边向外作等边 和等边 , 为 的中点,分别连接 , , , 与 相交于点G,著 ,下列四个结论:① ;②四边形 为平行四边形;③ ;④ .其中结论正确的是(填序号即可). 15. 菱形 在平面直角坐标系中的位置如图所示,已知 , , 点P是对角线 上的一个动点,当 周长最小时,则点P的坐标为 .
15. 菱形 在平面直角坐标系中的位置如图所示,已知 , , 点P是对角线 上的一个动点,当 周长最小时,则点P的坐标为 . 16. 如图,已知等边 ,顶点 在双曲线 上,点 的坐标为 .过点 作 交双曲线于点 ,过点 作 交x轴于点 ,得到第二个等 过点 作 交双曲线于点 ,过点 作 交x轴于点 ,得到第三个等边 、以此类推,…,则点 的横坐标为 .
16. 如图,已知等边 ,顶点 在双曲线 上,点 的坐标为 .过点 作 交双曲线于点 ,过点 作 交x轴于点 ,得到第二个等 过点 作 交双曲线于点 ,过点 作 交x轴于点 ,得到第三个等边 、以此类推,…,则点 的横坐标为 .
三、解答题
-
17. 先化简,再求值: ,其中x是不等式组的整数解 的整数解.18. 2020年5月份我市某初中为了提高学生“疫情防控”能力,组织了全校1500名学生参加线上“疫情防控”知识竞赛活动.知识竞赛总分100分,成绩取整数,赛后发现所有参赛学生的成绩均不低于50分,为了进一步了解本次“疫情防控”知识竞赛的成绩分布情况,随机抽取了部分学生的成绩进行整理,并将结果绘制了如下两幅不完整的统计图表,
成绩x(分)
频数
频率
a
0.10
16
0.08
30
b

请你根据以上统计图表中信息,回答下列问题:
(1)、这次随机抽取的部分学生有人:(2)、在表格中, , .(3)、请补全频数直方图:(4)、如果将得分转化为等级,规定: 评为D等级: 评为C等级: 评为B等级: 评为A等级.请估计全校参赛学生成绩被评为“B”等级的有多少人.19. 甲、乙、丙、丁四个人玩扑克牌游戏,他们先取出两张红心和两张黑桃共四张扑克牌,洗匀后背面朝上放在桌面上,每人抽取其中一张,拿到相同颜色扑克牌的两个人为游戏搭档.(1)、若甲抽取了一张扑克牌,那么这张扑克牌是红心的概率为 .(2)、若甲、乙两人各抽取了一张扑克牌, 求两人恰好成为游戏搭档的概率. (请用“画树状图”或“列表”方法求解)20. 某草莓生产基地在气温较低时,用装有恒温系统的大棚栽培一种新草莓.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度 与时间 之间的函数关系,其中线段 , 表示恒温系统开启阶段,线段 表示恒温系统关闭阶段.请根据图中信息解答下列问题:
 (1)、求这天大棚内的温度y与时间x( ) 之间的函数关系式;(2)、求恒温系统设定的恒定温度是多少度?(3)、若大棚内的温度低于15℃时,草莓会受到伤害.问在这天内恒温系统最多可以关闭多长时间就必须重新启动,才能避免草莓受到伤害.21. 某校数学活动小组为测量校园内旗杆高度,先制定了如下测量方案,使用工具有测角仪和皮尺,请帮助这个数学活动小组完成方案内容,求出旗杆AB的高度.
(1)、求这天大棚内的温度y与时间x( ) 之间的函数关系式;(2)、求恒温系统设定的恒定温度是多少度?(3)、若大棚内的温度低于15℃时,草莓会受到伤害.问在这天内恒温系统最多可以关闭多长时间就必须重新启动,才能避免草莓受到伤害.21. 某校数学活动小组为测量校园内旗杆高度,先制定了如下测量方案,使用工具有测角仪和皮尺,请帮助这个数学活动小组完成方案内容,求出旗杆AB的高度.数学活动方案
活动课题
测量学校旗杆的高度
活动地点
学校操场
活动时间
2020年5月30日
活动目的
运用所学数学知识及方法解决实际问题
方案示意图

测量步骤
⑴用 ▲ 测得
⑵用 ▲ 测得
米, 米.
计算过程
⑶如图,已知 , , 请根据具体测量数据,求出旗杆 的高度(结果精确到0.1).
(参考数据: , , )
解:
22. 如图,已知 是 的直径,点C,D在 上,连接 , 和 .过点D作 交 于点F, 与 相交于点E,P为 延长线上一点, 是 的切线. (1)、求证: :(2)、若点E是 中点, , ,求 的长.23. 为了让农民文化生活更加丰富多彩,某村决定修建文化广场,计划在一部分广场地面铺设相同大小规格的红色和白色地砖.经过市场调查,获取地砖市场相关信息如下:
(1)、求证: :(2)、若点E是 中点, , ,求 的长.23. 为了让农民文化生活更加丰富多彩,某村决定修建文化广场,计划在一部分广场地面铺设相同大小规格的红色和白色地砖.经过市场调查,获取地砖市场相关信息如下:购买数量低于5000块
购买数量不低于5000块
红色地砖
原价销售
原价的八折销售
白色地砖
原价销售
原价的九折销售
(1)、如果购买红色地砖40块,白色地砖60块,共需付款920元:如果购买红色地砖50块,白色地砖35块,共需付款750元求红色地砖与白色地砖的原价各多少元?(2)、经过测算,修建这个文化广场需要购买两种地砖共计12000块,其中白色地砖的数量不少于红色地砖的数量的一半,且白色地砖的数量不多于7000块,求购买红色地砖与白色地砖各多少块时,付款最少.24. 已知 和 , , , , 连接 , .(1)、如图①,当点E在 边上时,试判断线段 , 之间的关系是 . (2)、将上图中的 绕点A旋转至如图所示位置时,探究线段 . 之间的关系,并说明理由:
(2)、将上图中的 绕点A旋转至如图所示位置时,探究线段 . 之间的关系,并说明理由: (3)、将图①中的 绕点A旋转至 与直线 垂直,直线 交直线 于点F,若 , ,请直接写出线段 的长度.
(3)、将图①中的 绕点A旋转至 与直线 垂直,直线 交直线 于点F,若 , ,请直接写出线段 的长度.