辽宁省鞍山市铁西区2019-2020学年九年级下学期数学6月月考试卷
试卷更新日期:2021-03-15 类型:月考试卷
一、单选题
-
1.
一个几何体的三视图如图所示,则这个几何体是( )
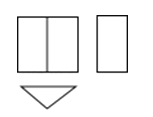 A、
A、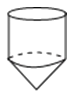 B、
B、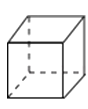 C、
C、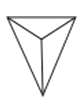 D、
D、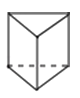 2. 2019年10月1日,庆祝中华人民共和国成立70周年大会在北京天安门广场隆重举行.10月3日微博观看互动量累计达到19280000次,将19280000用科学记数法表示为( )A、1.928 × 104 B、1928×104 C、1.928 × 107 D、0.1928 × 1083. 在一个长 分米、宽 分米、高 分米的长方体容器中,水面高 分米,把一个实心铁块缓慢浸入这个容器的水中,能够表示铁块浸入水中的体积y(单位:立方分米)与水面上升高度x(单位:分米)之间关系的图象的是( )A、
2. 2019年10月1日,庆祝中华人民共和国成立70周年大会在北京天安门广场隆重举行.10月3日微博观看互动量累计达到19280000次,将19280000用科学记数法表示为( )A、1.928 × 104 B、1928×104 C、1.928 × 107 D、0.1928 × 1083. 在一个长 分米、宽 分米、高 分米的长方体容器中,水面高 分米,把一个实心铁块缓慢浸入这个容器的水中,能够表示铁块浸入水中的体积y(单位:立方分米)与水面上升高度x(单位:分米)之间关系的图象的是( )A、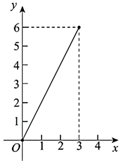 B、
B、 C、
C、 D、
D、 4. 某班七个兴趣小组人数如下:5,6,6,x,7,8,9,已知这组数据的平均数是7,则这组数据的中位数是( )A、6 B、6.5 C、7 D、85. 某工厂第二季度的产值比第一季度的产值增长了x%,第三季度的产值又比第二季度的产值增长了x%,则第三季度的产值比第一季度的产值增长了( )A、2x% B、1+2x% C、(1+x%)x% D、(2+x%)x%6. 如图,⊙O是正五边形ABCDE的外接圆,点P是 的一点,则∠CPD的度数是( )
4. 某班七个兴趣小组人数如下:5,6,6,x,7,8,9,已知这组数据的平均数是7,则这组数据的中位数是( )A、6 B、6.5 C、7 D、85. 某工厂第二季度的产值比第一季度的产值增长了x%,第三季度的产值又比第二季度的产值增长了x%,则第三季度的产值比第一季度的产值增长了( )A、2x% B、1+2x% C、(1+x%)x% D、(2+x%)x%6. 如图,⊙O是正五边形ABCDE的外接圆,点P是 的一点,则∠CPD的度数是( )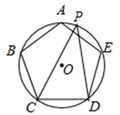 A、30° B、36° C、45° D、72°7. 如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是
A、30° B、36° C、45° D、72°7. 如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
 A、 B、 C、5 D、68. 如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OE•OP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE= ,其中正确的结论是( )
A、 B、 C、5 D、68. 如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OE•OP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE= ,其中正确的结论是( )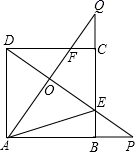 A、①③ B、①②③ C、①③④ D、①②③④
A、①③ B、①②③ C、①③④ D、①②③④二、填空题
-
9. 小明先将图1中的矩形沿虚线剪开分成四个全等的小矩形,再将这四个小矩形拼成如图2的正方形,那么图1中矩形的面积为 .
 10. 因式分解: .11. 若关于x的一元二次方程kx2+2(k+1)x+k-1=0有两个实数根,则k的取值范围是 .12. 若圆锥的底面半径为3cm,母线长是5cm,则它的侧面展开图的面积为 cm2 .13. 如图,在矩形ABCD中,AB=12,BC=10,M是AD边的中点,N是AB边上的动点,将△AMN沿MN所在直线折叠,得到△ ,连接 ,则 的最小值是 .
10. 因式分解: .11. 若关于x的一元二次方程kx2+2(k+1)x+k-1=0有两个实数根,则k的取值范围是 .12. 若圆锥的底面半径为3cm,母线长是5cm,则它的侧面展开图的面积为 cm2 .13. 如图,在矩形ABCD中,AB=12,BC=10,M是AD边的中点,N是AB边上的动点,将△AMN沿MN所在直线折叠,得到△ ,连接 ,则 的最小值是 .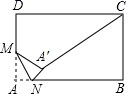 14. 如图,等腰Rt△ABP的斜边AB=2,点M、N在斜边AB上.若△PMN是等腰三角形且底角正切值为2,则MN= .
14. 如图,等腰Rt△ABP的斜边AB=2,点M、N在斜边AB上.若△PMN是等腰三角形且底角正切值为2,则MN= . 15. 如图,点A1在直线l1:y= x上,过点A1作x轴的平行线交直线l2:y= x于点B1 ,
15. 如图,点A1在直线l1:y= x上,过点A1作x轴的平行线交直线l2:y= x于点B1 ,过点B1作l2的垂线交l1于点A2 , 过点A2作x轴的平行线交直线l2于点B2 , 过点B2作l2的垂线交l1于点A3 , 过点A3作x轴的平行线交直线l2于点B3 , ……,过点B1 , B2 , B3 , ……,分别作l1的平行线交A2B2于点C1 , 交A3B3于点C2 , 交A4B4于点C3 , ……,按此规律继续下去,若OA1=1,则点 的坐标为 .
 16. 如图点P为双曲线 上一动点.连接OP并延长到点A , 使 ,过点A作x轴的垂线,垂足为B , 交双曲线于点C.当 时,连接PC , 将 沿直线PC进行翻折,则翻折后的 与四边形BOPC的重叠部分(图中阴影部分)的面积是
16. 如图点P为双曲线 上一动点.连接OP并延长到点A , 使 ,过点A作x轴的垂线,垂足为B , 交双曲线于点C.当 时,连接PC , 将 沿直线PC进行翻折,则翻折后的 与四边形BOPC的重叠部分(图中阴影部分)的面积是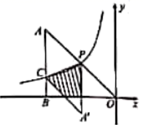
三、解答题
-
17. 先化简,再求值: ,其中 的值满足方程: .18. 如图,△ABC的三个顶点坐标分别为A(2,3),B(3,1),C(5,4).
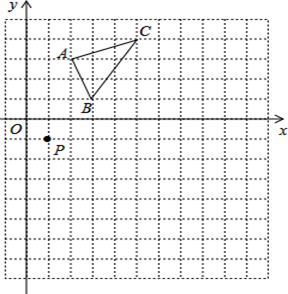
⑴画出△ABC关于x轴对称的△A1B1C1;
⑵以点P(1,﹣1)为位似中心,在如图所示的网格中画出△A1B1C1的位似图形△A2B2C2 , 使△A2B2C2与△A1B1C1的相似比为2:1;
⑶画出△ABC绕点C逆时针旋转90°的△A′B′C′,并写出线段BC扫过的面积
19. 某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机抽取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:根据上述信息完成下列问题:
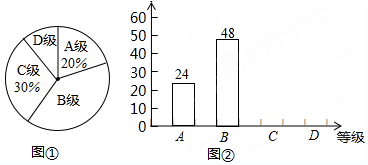 (1)、在这次抽样调查中,共抽查了多少名学生?(2)、请在图②中把条形统计图补充完整;(3)、求出扇形统计图中“D级”部分所对应的扇形圆心角的大小;(4)、已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?20. “2020盐城国际半程马拉松”的赛事共有三项:A、“半程马拉松”、B、“10公里”、C、“迷你马拉松”.小明和小华参加了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组.(1)、小明被分配到“迷你马拉松”项目组的概率为;(2)、请用表格或树状图列出所有可能情况,求小明和小华被分配到不同项目组的概率.21. 如图,海中有一小岛P,在距小岛P的 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
(1)、在这次抽样调查中,共抽查了多少名学生?(2)、请在图②中把条形统计图补充完整;(3)、求出扇形统计图中“D级”部分所对应的扇形圆心角的大小;(4)、已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?20. “2020盐城国际半程马拉松”的赛事共有三项:A、“半程马拉松”、B、“10公里”、C、“迷你马拉松”.小明和小华参加了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组.(1)、小明被分配到“迷你马拉松”项目组的概率为;(2)、请用表格或树状图列出所有可能情况,求小明和小华被分配到不同项目组的概率.21. 如图,海中有一小岛P,在距小岛P的 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?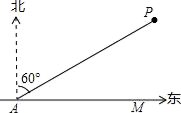 22. 如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C坐标为(﹣1,0),tan∠ACO=2.一次函数y=kx+b的图象经过点B、C , 反比例函数y= 的图象经过点B .
22. 如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C坐标为(﹣1,0),tan∠ACO=2.一次函数y=kx+b的图象经过点B、C , 反比例函数y= 的图象经过点B .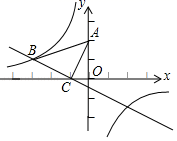 (1)、求一次函数关系式和反比例函数的关系式;(2)、当x<0时,kx+b﹣ <0的解集为;(3)、若x轴上有两点E、F , 点E在点F的左边,且EF=1.当四边形ABEF周长最小时,请直接写出点E的横坐标为 .23. 如图,△ABC内接于⊙O , AB是⊙O的直径,弦CD与AB交于点E , 连接AD , 过点A作直线MN , 使∠MAC=∠ADC .
(1)、求一次函数关系式和反比例函数的关系式;(2)、当x<0时,kx+b﹣ <0的解集为;(3)、若x轴上有两点E、F , 点E在点F的左边,且EF=1.当四边形ABEF周长最小时,请直接写出点E的横坐标为 .23. 如图,△ABC内接于⊙O , AB是⊙O的直径,弦CD与AB交于点E , 连接AD , 过点A作直线MN , 使∠MAC=∠ADC .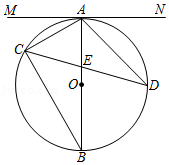 (1)、求证:直线MN是⊙O的切线.(2)、若sin∠ADC= ,AB=8,AE=3,求DE的长.24. 某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格(元/个)的函数关系如图所示.
(1)、求证:直线MN是⊙O的切线.(2)、若sin∠ADC= ,AB=8,AE=3,求DE的长.24. 某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格(元/个)的函数关系如图所示. (1)、当30≤x≤60时,求y与x的函数关系式;(2)、求出该厂生产销售这种产品的纯利润w(万元)与销售价格x(元/个)的函数关系式;(3)、销售价格应定为多少元时,获得利润最大,最大利润是多少?25.
(1)、当30≤x≤60时,求y与x的函数关系式;(2)、求出该厂生产销售这种产品的纯利润w(万元)与销售价格x(元/个)的函数关系式;(3)、销售价格应定为多少元时,获得利润最大,最大利润是多少?25.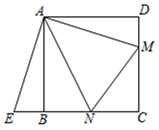

图① 图②
图③
(操作发现)
如图①,在正方形ABCD中,点N、M分别在边BC、CD上,连结AM、AN、MN .
∠MAN=45°,将△AMD绕点A顺时针旋转90°,点D与点B重合,得到△ABE . 易证:△ANM≌△ANE , 从而得DM+BN=MN .
(1)、(实践探究)在图①条件下,若CN=3,CM=4,则正方形ABCD的边长是 .
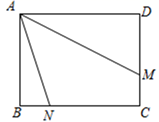
(2)、如图②,点M、N分别在边CD、AB上,且BN=DM . 点E、F分别在BM、DN上,∠EAF=45°,连接EF , 猜想三条线段EF、BE、DF之间满足的数量关系,并说明理由.(3)、(拓展)如图③,在矩形ABCD中,AB=3,AD=4,点M、N分别在边DC、BC上,连结AM,AN , 已知∠MAN=45°,BN=1,求DM的长.
26. 如图1,抛物线y=﹣x2+bx+c(a≠0)的顶点为C , 交x轴于A 、B 两点,交y轴于点D .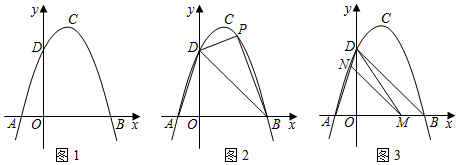 (1)、求抛物线的解析式;并直接写出点C的坐标.(2)、如图2,点P为直线BD上方抛物线上一点,作PE⊥BD于点E,AF⊥BD于点F若 ,请求出点P的坐标.(3)、如图3,M为线段AB上的一点,过点M作MN∥BD , 交线段AD于点N , 连接MD , 若△DNM∽△BMD , 请求出点M的坐标.
(1)、求抛物线的解析式;并直接写出点C的坐标.(2)、如图2,点P为直线BD上方抛物线上一点,作PE⊥BD于点E,AF⊥BD于点F若 ,请求出点P的坐标.(3)、如图3,M为线段AB上的一点,过点M作MN∥BD , 交线段AD于点N , 连接MD , 若△DNM∽△BMD , 请求出点M的坐标.