江西省赣州市石城县2019-2020学年九年级下学期数学第一次月考试卷
试卷更新日期:2021-03-15 类型:月考试卷
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 如图所示的几何体的俯视图是( )
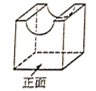 A、
A、 B、
B、 C、
C、 D、
D、 3. 为备战中考体育一分钟跳绳项目考试,同学们坚持通过每天记录成绩来促进提高.下图是某班全体学生一分钟跳绳成绩记录表:
3. 为备战中考体育一分钟跳绳项目考试,同学们坚持通过每天记录成绩来促进提高.下图是某班全体学生一分钟跳绳成绩记录表:成绩/次
150
160
168
170
175
178
180
人数
1
5
4
6
4
8
4
该班学生跳绳成绩的众数与中位数分别为( )
A、170,170 B、178,172.5 C、170,175 D、178,1704. 一元一次不等式组 的解集在数轴上表示为( ).A、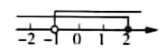 B、
B、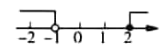 C、
C、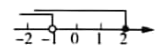 D、
D、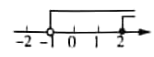 5. 如图,在⊙ 中,半径 垂直弦 于 ,点 在⊙ 上, ,则半径 等于( )
5. 如图,在⊙ 中,半径 垂直弦 于 ,点 在⊙ 上, ,则半径 等于( )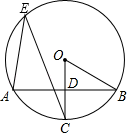 A、 B、 C、 D、6. 抛物线 的对称轴是直线 ,且过点(1,0).顶点位于第二象限,其部分图像如图所示,给出以下判断:
A、 B、 C、 D、6. 抛物线 的对称轴是直线 ,且过点(1,0).顶点位于第二象限,其部分图像如图所示,给出以下判断:① 且 ;② ;③ ;④ ;⑤直线 与抛物线 两个交点的横坐标分别为 ,则 .其中正确的个数有( )
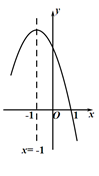 A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个二、填空题
-
7. 使式子 成立的x的取值范围是.8. 港珠澳大桥被英国《卫报》誉为“新世界七大奇迹”之一,它是世界总体跨度最长的跨海大桥,全长55000米.数字55000用科学记数法表示为.9. 《九章算术》是中国传统数学最重要的著作之一.书中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数几何?”意思是:“有若干人共同出钱买鸡,如果每人出九钱,那么多了十一钱;如果每人出六钱,那么少了十六钱.问:共有几个人?”设共有 个人共同出钱买鸡,根据题意,可列一元一次方程为.10. 如图,点 E 为是正方形 ABCD 的边 DC 上一点,把△ADE 绕点 A 顺时针旋转 90°到△ABF 的位置,若四边形 AECF 的面积为 36,DE=2,则 AE 的长为 .
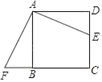 11. 一元二次方程x2﹣3x﹣2=0的两根为x1 , x2 , 则x12+3x2+x1x2﹣2的值为 .12. 如图,在▱ABCD中,已知AD=10cm,tanB=2,AE⊥BC于点E,且AE=4cm,点P是BC边上一动点.若△PAD为直角三角形,则BP的长为
11. 一元二次方程x2﹣3x﹣2=0的两根为x1 , x2 , 则x12+3x2+x1x2﹣2的值为 .12. 如图,在▱ABCD中,已知AD=10cm,tanB=2,AE⊥BC于点E,且AE=4cm,点P是BC边上一动点.若△PAD为直角三角形,则BP的长为
三、解答题
-
13.(1)、计算: ;(2)、如图,点B、D在线段AE上,AD=BE,AC∥EF,∠C=∠F,求证:BC=DF.
 14. 先化简,再求值: ,然后从0,1,2三个数中选择一个恰当的数代入求值.15. 第24届冬奥会将于2022年在北京和张家口举行,冬奥会的项目有滑雪(如高山滑雪、单板滑雪等),滑冰(如速度滑冰、花样滑冰等),冰球,冰壶等.如图,有4张形状、大小、质地均相同的卡片,正面分别印有单板滑雪、速度滑冰、冰球、冰壶4种不同的图案,背面完全相同.现将这4张卡片洗匀后正面向下放在桌子上.
14. 先化简,再求值: ,然后从0,1,2三个数中选择一个恰当的数代入求值.15. 第24届冬奥会将于2022年在北京和张家口举行,冬奥会的项目有滑雪(如高山滑雪、单板滑雪等),滑冰(如速度滑冰、花样滑冰等),冰球,冰壶等.如图,有4张形状、大小、质地均相同的卡片,正面分别印有单板滑雪、速度滑冰、冰球、冰壶4种不同的图案,背面完全相同.现将这4张卡片洗匀后正面向下放在桌子上. (1)、从中随机抽取1张,抽出的卡片上恰好是滑雪项目图案的概率是.(2)、若印有单板滑雪、速度滑冰、冰球、冰壶4种不同图案的卡片分别用A,B,C,D表示,从中随机抽取两张,试用画树状图或列表的方法求出印有冰球图案的卡片被抽中的概率.16. 如图所示的图形是一个轴对称图形,且每个角都是直角,小明用n个这样的图形,按照如图(2)所示的方法玩拼图游戏,两两相扣,相互间不留空隙.
(1)、从中随机抽取1张,抽出的卡片上恰好是滑雪项目图案的概率是.(2)、若印有单板滑雪、速度滑冰、冰球、冰壶4种不同图案的卡片分别用A,B,C,D表示,从中随机抽取两张,试用画树状图或列表的方法求出印有冰球图案的卡片被抽中的概率.16. 如图所示的图形是一个轴对称图形,且每个角都是直角,小明用n个这样的图形,按照如图(2)所示的方法玩拼图游戏,两两相扣,相互间不留空隙.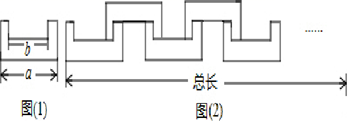 (1)、当n=5时,小明拼出来的图形总长度是.(用含a、b的式子表示)(2)、当a=4,b=3时,小明用n个这样的图形拼出来的图形总长度为28,求n的值.17. 请仅用无刻度的直尺,根据下列条件分别在图(1),图(2),(3)中作出△ABC的边AB上的高CD.
(1)、当n=5时,小明拼出来的图形总长度是.(用含a、b的式子表示)(2)、当a=4,b=3时,小明用n个这样的图形拼出来的图形总长度为28,求n的值.17. 请仅用无刻度的直尺,根据下列条件分别在图(1),图(2),(3)中作出△ABC的边AB上的高CD.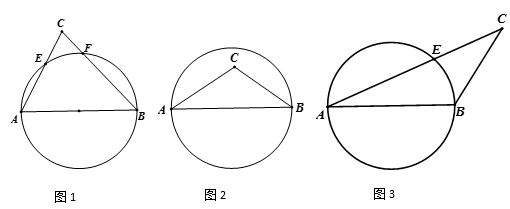 (1)、如图(1),以锐角三角形ABC的边AB为直径的圆,与边BC、AC分别交于点E、F;(2)、如图(2),以等腰三角形ABC的底边AB为直径的圆,顶点C在圆内;(3)、如图(3),以钝角三角形ABC的一短边AB为直径的圆,与最长的边AC相交于点E.18. 为了解某县建档立卡贫困户对精准扶贫政策落实的满意度,现从全县建档立卡贫困户中随机抽取了部分贫困户进行了调查(把调查结果分为四个等级:A级:非常满意:B级满意;C级:基本满意:D级:不满意),并将调查结果绘制成如两幅不完整的统计图,请根据统计图中的信息解决下列问题:
(1)、如图(1),以锐角三角形ABC的边AB为直径的圆,与边BC、AC分别交于点E、F;(2)、如图(2),以等腰三角形ABC的底边AB为直径的圆,顶点C在圆内;(3)、如图(3),以钝角三角形ABC的一短边AB为直径的圆,与最长的边AC相交于点E.18. 为了解某县建档立卡贫困户对精准扶贫政策落实的满意度,现从全县建档立卡贫困户中随机抽取了部分贫困户进行了调查(把调查结果分为四个等级:A级:非常满意:B级满意;C级:基本满意:D级:不满意),并将调查结果绘制成如两幅不完整的统计图,请根据统计图中的信息解决下列问题: (1)、本次抽样调查测试的建档立卡贫困户的总户数是;(2)、图①中,∠α的度数是 , 并把图②条形统计图补充完整;(3)、某县建档立卡贫困户有10000户,如果全部参加这次满意度调查,请估计非常满意的户数约为多少户?19. 如图1所示的是一种折叠门,已知门框的宽度AD=2米,两扇门的大小相同(即AB=CD),且AB+CD=AD,现将右边的门CDD1C1绕门轴DD1向外面旋转67°(如图2).(参考数据:sin67°≈0.92,cos67°≈0.39, tan29.6°≈0.57,tan19.6°≈0.36,sin29.6°≈0.49)
(1)、本次抽样调查测试的建档立卡贫困户的总户数是;(2)、图①中,∠α的度数是 , 并把图②条形统计图补充完整;(3)、某县建档立卡贫困户有10000户,如果全部参加这次满意度调查,请估计非常满意的户数约为多少户?19. 如图1所示的是一种折叠门,已知门框的宽度AD=2米,两扇门的大小相同(即AB=CD),且AB+CD=AD,现将右边的门CDD1C1绕门轴DD1向外面旋转67°(如图2).(参考数据:sin67°≈0.92,cos67°≈0.39, tan29.6°≈0.57,tan19.6°≈0.36,sin29.6°≈0.49)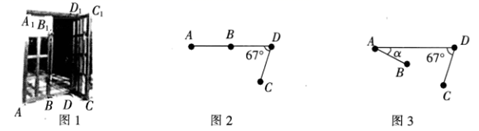 (1)、求点C到AD的距离.(2)、将左边的门ABB1A1绕门轴AA1向外面旋转,设旋转角为α(如图3),问α为多少时,点B,C之间的距离最短?20. 如图,在平面直角坐标系xOy中,直线y=2x+b经过点A(﹣1,0),与y轴正半轴交于B点,与反比例函数 (x>0)交于点C , 且BC=2AB , BD∥x轴交反比例函数 (x>0)于点D , 连接AD .
(1)、求点C到AD的距离.(2)、将左边的门ABB1A1绕门轴AA1向外面旋转,设旋转角为α(如图3),问α为多少时,点B,C之间的距离最短?20. 如图,在平面直角坐标系xOy中,直线y=2x+b经过点A(﹣1,0),与y轴正半轴交于B点,与反比例函数 (x>0)交于点C , 且BC=2AB , BD∥x轴交反比例函数 (x>0)于点D , 连接AD .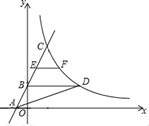 (1)、求b , k的值;(2)、求△ABD的面积;(3)、若E为线段BC上一点,过点E作EF∥BD , 交反比例函数 (x>0)于点F , 且EF= BD , 求点F的坐标.21. 如图1,圆内接四边形ABCD,AD=BC,AB是⊙O的直径.
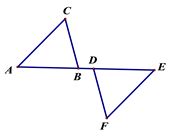
(1)、求b , k的值;(2)、求△ABD的面积;(3)、若E为线段BC上一点,过点E作EF∥BD , 交反比例函数 (x>0)于点F , 且EF= BD , 求点F的坐标.21. 如图1,圆内接四边形ABCD,AD=BC,AB是⊙O的直径. (1)、求证:AB∥CD;(2)、如图2,连接OD,作∠CBE=2∠ABD,BE交DC的延长线于点E,若AB=6,AD=2,求CE的长;(3)、如图3,延长OB使得BH=OB,DF是⊙O的直径,连接FH,若BD=FH,求证:FH是⊙O的切线.22.
(1)、求证:AB∥CD;(2)、如图2,连接OD,作∠CBE=2∠ABD,BE交DC的延长线于点E,若AB=6,AD=2,求CE的长;(3)、如图3,延长OB使得BH=OB,DF是⊙O的直径,连接FH,若BD=FH,求证:FH是⊙O的切线.22.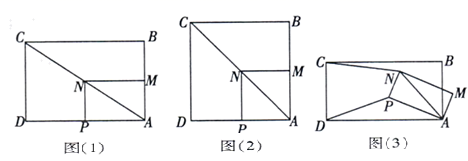
如图(1),在矩形ABCD中,AD=nAB,点M,P分别在边AB,AD上(均不与端点重合),且AP=nAM,以AP和AM为邻边作矩形AMNP,连接AN,CN.
(1)、(问题发现)如图(2),当n=1时,BM与PD的数量关系为 , CN与PD的数量关系为.
(2)、(类比探究)如图(3),当n=2时,矩形AMNP绕点A顺时针旋转,连接PD,则CN与PD之间的数量关系是否发生变化?若不变,请就图(3)给出证明;若变化,请写出数量关系,并就图(3)说明理由.
(3)、(拓展延伸)在(2)的条件下,已知AD=4,AP=2,当矩形AMVP旋转至C,N,M三点共线时,请直接写出线段CN的长
23. 已知抛物线 和抛物线 (n为正整数).(1)、抛物线 与x轴的交点坐标为.顶点坐标为.(2)、当n=1时,请解答下列问题:抛物线 与x轴的交点坐标为.顶点坐标为.请写出抛物线y, 的一条相同的性质.
(3)、当直线 与抛物线y, ,共有4个交点时,求m的取值范围(4)、若直线y=k(k<0)与抛物线y, 共有4个交点,从左至右依次标记为点A,B,C,D,当AB=BC=CD时,求出k,n之间满足的关系式.