河北省石家庄2019-2020学年九年级下学期数学4月月考试卷
试卷更新日期:2021-03-15 类型:月考试卷
一、单选题
-
1. 如图,在数轴上,若点B表示一个负数,则原点可以是( )
 A、点E B、点D C、点C D、点A2. 要将等式 进行一次变形,得到x=-2,下列做法正确的是( )A、等式两边同时加 B、等式两边同时乘以 C、等式两边同时除以 D、等式两边同时乘以3. 如图,在 中, 是 的中点,则下列结论不一定正确的是( )
A、点E B、点D C、点C D、点A2. 要将等式 进行一次变形,得到x=-2,下列做法正确的是( )A、等式两边同时加 B、等式两边同时乘以 C、等式两边同时除以 D、等式两边同时乘以3. 如图,在 中, 是 的中点,则下列结论不一定正确的是( ) A、 B、 C、 D、4. 下列计算,正确的是( )A、 B、 C、 D、5. 下列由一个正方形和两个相同的等腰直角三角形组成的图形中,为中心对称图形的是( )A、
A、 B、 C、 D、4. 下列计算,正确的是( )A、 B、 C、 D、5. 下列由一个正方形和两个相同的等腰直角三角形组成的图形中,为中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 世界上最薄的纳米材料其理论厚度是 ,该数据用科学记数法表示为 ,则a的值为( )A、 B、 C、 D、7. 对于 个数据,平均数为 ,则去掉最小数据 和最大数据 后得到一组新数据的平均数( )A、大于 B、小于 C、等于 D、无法确定8. 已知实数 互为倒数,且 ,则 的值为( )A、 B、 C、 D、9. 如图是某河坝横断面示意图, 迎水坡, 为背水坡,过点A作水平面的垂线 ,设斜坡 的坡度为 ,坡角为 ,斜坡 的坡度为 ,坡角为 ,则下列结论正确的是( )
6. 世界上最薄的纳米材料其理论厚度是 ,该数据用科学记数法表示为 ,则a的值为( )A、 B、 C、 D、7. 对于 个数据,平均数为 ,则去掉最小数据 和最大数据 后得到一组新数据的平均数( )A、大于 B、小于 C、等于 D、无法确定8. 已知实数 互为倒数,且 ,则 的值为( )A、 B、 C、 D、9. 如图是某河坝横断面示意图, 迎水坡, 为背水坡,过点A作水平面的垂线 ,设斜坡 的坡度为 ,坡角为 ,斜坡 的坡度为 ,坡角为 ,则下列结论正确的是( )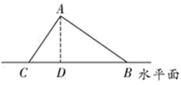 A、 B、 C、 D、10. 如图,已知点 分别在 的边 上,若 ,由作图痕迹可得, 的最小值是( )
A、 B、 C、 D、10. 如图,已知点 分别在 的边 上,若 ,由作图痕迹可得, 的最小值是( ) A、 B、 C、 D、11. 已知 ( 均为常数,且 ),则一元二次方程根 的情况是( )A、有两个不相等的实数根 B、有两个实数根 C、有两个相等的实数根 D、无实数根12. 若 的值小于 ,则x的取值范围为( )A、 B、 C、 D、13. 如图,在 的正方形网格中,每个小正方形的边长均为1,四边形 的周长记为c,若 (a为正整数),则a的值为( )
A、 B、 C、 D、11. 已知 ( 均为常数,且 ),则一元二次方程根 的情况是( )A、有两个不相等的实数根 B、有两个实数根 C、有两个相等的实数根 D、无实数根12. 若 的值小于 ,则x的取值范围为( )A、 B、 C、 D、13. 如图,在 的正方形网格中,每个小正方形的边长均为1,四边形 的周长记为c,若 (a为正整数),则a的值为( ) A、4 B、5 C、6 D、714. 如图为由若干个大小相同的正方体组成的几何体的左视图和俯视图,则它的主视图不可能是( )
A、4 B、5 C、6 D、714. 如图为由若干个大小相同的正方体组成的几何体的左视图和俯视图,则它的主视图不可能是( ) A、
A、 B、
B、 C、
C、 D、
D、 15. 如图,已知点O是 的外心,连接 并延长交 于点D,若 ,则 的度数为( )
15. 如图,已知点O是 的外心,连接 并延长交 于点D,若 ,则 的度数为( ) A、 B、 C、 D、16. 对于题目:在平面直角坐标系中,直线 分别与x轴、y轴交于 两点,过点A且平行y轴的直线与过点B且平行x轴的直线相交于点C,若抛物线 与线段 有唯一公共点,求a的取值范围.甲的计算结果是 ;乙的计算结果是 ,则( )A、甲的结果正确 B、乙的结果正确 C、甲与乙的结果合在一起正确 D、甲与乙的结果合在一起也错误
A、 B、 C、 D、16. 对于题目:在平面直角坐标系中,直线 分别与x轴、y轴交于 两点,过点A且平行y轴的直线与过点B且平行x轴的直线相交于点C,若抛物线 与线段 有唯一公共点,求a的取值范围.甲的计算结果是 ;乙的计算结果是 ,则( )A、甲的结果正确 B、乙的结果正确 C、甲与乙的结果合在一起正确 D、甲与乙的结果合在一起也错误二、填空题
-
17. 计算 × 的值是 .18. 观察下列一组数据,其中绝对值依次增大2,且每两个正数之间有两个负数:1,-3,-5,7,-9,-11,13,-15,...;则第10个数是;第3n个数是 , n为正整数).19. 如图,过正六边形 的顶点D作一条直线 于点D,分别延长 交直线l于点 ,则 ;若正六边形 的面积为6,则 的面积为 .

三、解答题
-
20. 在实数范围内,对于任意实数 规定一种新运算: ,例如: .(1)、计算:(2)、若 ,求x的值;(3)、若 的最小值为a,求a的值.21. 在证明定理“三角形的中位线平行于第三边,且等于第三边的一半”时,小明给出如下部分证明过程.
已知:在 中, 分别是边 的中点.
求证:……..
证明:如图,延长 到点F,使 ,连接 ,
···
 (1)、补全求证:(2)、请根据添加的辅助线,写出完整的证明过程;(3)、若 求边AB的取值范围.22. 在抗击新型冠状病毒肺炎战役中,某市党员积极响应国家号召参加志愿者活动,为人民服务,现随机抽查部分党员一个月来参加志愿者活动的次数,并绘制成如下尚不完整的条形统计图(图1)和扇形统计图(图2).
(1)、补全求证:(2)、请根据添加的辅助线,写出完整的证明过程;(3)、若 求边AB的取值范围.22. 在抗击新型冠状病毒肺炎战役中,某市党员积极响应国家号召参加志愿者活动,为人民服务,现随机抽查部分党员一个月来参加志愿者活动的次数,并绘制成如下尚不完整的条形统计图(图1)和扇形统计图(图2). (1)、“4次”所在扇形的圆心角度数是 , 请补全 条形统计图;(2)、若从抽在的党员中随机选择一位接受媒体的采访,求该党员一个月来参加志愿者活动次数不少于3次的概率;(3)、设随机抽查的党员一个月来参加志愿者活动次数的中位数为a,若去掉一部分党员参加志愿者活动的次数后,得到一组新数据的众数为b,当 时,求最少去掉了几名党员参加志愿者活动的次数.23. 如图,在矩形 中,点E是边 上一点(不与点 重合),点F是 延长线上一点,且 ,连接 .
(1)、“4次”所在扇形的圆心角度数是 , 请补全 条形统计图;(2)、若从抽在的党员中随机选择一位接受媒体的采访,求该党员一个月来参加志愿者活动次数不少于3次的概率;(3)、设随机抽查的党员一个月来参加志愿者活动次数的中位数为a,若去掉一部分党员参加志愿者活动的次数后,得到一组新数据的众数为b,当 时,求最少去掉了几名党员参加志愿者活动的次数.23. 如图,在矩形 中,点E是边 上一点(不与点 重合),点F是 延长线上一点,且 ,连接 . (1)、求证:(2)、连接 ,其中
(1)、求证:(2)、连接 ,其中①当四边形 是菱形时,求线段 与线段 之间的距离;
②若点l是 的内心,连接 ,直接写出 的取值范围.
24. 在平面直角坐标系中,我们定义:横坐标与纵坐标均为整数的点为整点如图,已知双曲线 经过点 ,记双曲线与两坐标轴之间的部分为G(不含双曲线与坐标轴). (1)、求k的值;(2)、求G内整点的个数;(3)、设点 在直线 上,过点B分别作平行于x轴y轴的直线,交双曲线 于点 ,记线段 、双曲线所围成的区域为W,若W内部(不包括边界)不超过8个整点,求m的取值范围.25. 如图1,在正方形 中, ,点 在边 上,且 ,以点O为圆心, 为半径在其左侧作半圆O,分别交 )于点G,交 的延长线于点F.
(1)、求k的值;(2)、求G内整点的个数;(3)、设点 在直线 上,过点B分别作平行于x轴y轴的直线,交双曲线 于点 ,记线段 、双曲线所围成的区域为W,若W内部(不包括边界)不超过8个整点,求m的取值范围.25. 如图1,在正方形 中, ,点 在边 上,且 ,以点O为圆心, 为半径在其左侧作半圆O,分别交 )于点G,交 的延长线于点F.
 (1)、AG=;(2)、如图2,将半圆O绕点E逆时针旋转 ,点O的对应点为 ,点F的对应点为 ;设M为半圆 上一点.
(1)、AG=;(2)、如图2,将半圆O绕点E逆时针旋转 ,点O的对应点为 ,点F的对应点为 ;设M为半圆 上一点.①当点 落在 边上时,求点M与线段 之间的最短距离;
②当半圆 交 于 两点时,若 的长为 ,求此时半圆 与正方形 重叠部分的面积;
③当半圆 与正方形 的边相切时,设切点为N,直接写出 的值.
26. 某公司为了宣传一种新产品,在某地先后举行40场产品促销会,已知该产品每台成本为10万元,设第x场产品的销售量为y (台),在销售过程中获得以下信息:信息1:已知第一场销售产品49台,然后每增加一场,产品就少卖出1台;
信息2:产品的每场销售单价p(万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次x成正比,第21场--第40场浮动价与销售场次x成反比,经过统计,得到如下数据:
x(场)
3
10
25
p(万元)
10.6
12
14.2
(1)、求y与x之间满足的函数关系式;(2)、当产品销售单价为13万元时,求销售场次是第几场?(3)、在这40场产品促销会中,哪一场获得的利润最大,最大利润是多少?