河北省邯郸市复兴区2019-2020学年九年级下学期数学第一次月考试卷
试卷更新日期:2021-03-15 类型:月考试卷
一、单选题
-
1. 下列各数中,属于无理数的是( )A、 B、1.4141414 C、 D、2. 花粉的质量很小,一粒某种植物花粉的质量约为0.000037毫克,已知1克=1000毫克,那么0.000037毫克可用科学记数法表示为( )A、3.7×10﹣5克 B、3.7×10﹣6克 C、37×10﹣7克 D、3.7×10﹣8克3. 在数轴上,点A,B在原点O的两侧,分别表示数a , 2,将点A向右平移1个单位长度,得到点C.若CO=BO,则a的值为( )A、-3 B、-2 C、-1 D、14. 下列关系式中,y是x反比例函数的是( )A、y= x B、y=- C、y=3x2 D、y=6x+15. 下列各式中,自变量x的取值范围是x≥2的是( )A、y=x-2 B、y= C、y= · D、y=x2-46. 解分式方程 时,去分母变形正确的是( )A、 B、 C、 D、7. 已知二元一次方程组 ,则 的值是( )A、 B、5 C、 D、68. 已知 , ,其中 , 为正整数,则 ( )A、 B、 C、 D、9. A.B两地相距180km,新修的高速公路开通后,在A,B两地间行驶的长途客车平均车速提高了50%,而从A地到B地的时间缩短了1h.若设原来的平均车速为xkm/h,则根据题意可列方程为( )A、 B、 C、 D、10. 下列关于抛物线 有关性质的说法,正确的是( )A、其图象的开口向下 B、其图象的对称轴为 C、其最大值为1 D、当 时,y随x的增大而减小11. 若 ,则正比例函数 与反比例函数 在同一坐标系中的大致图象可能是( )
A、 B、
B、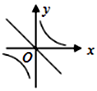 C、
C、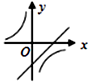 D、
D、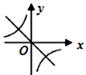 12. 如图,直线a∥b,直线c与a、b都相交,从所标识的∠1、∠2、∠3、∠4、∠5这五个角中任意选取两个角,则所选取的两个角互为补角的概率是( )
12. 如图,直线a∥b,直线c与a、b都相交,从所标识的∠1、∠2、∠3、∠4、∠5这五个角中任意选取两个角,则所选取的两个角互为补角的概率是( ) A、 B、 C、 D、
A、 B、 C、 D、
二、填空题
-
13. 若点(m+3,-4)和点(-4,n+1)关于x轴对称,则m+n=14. 分解因式: =15. 请写出一个图像过(2,3)和(3,2)两点函数解析式16. 某校艺术班的同学,每人都会弹钢琴或古筝,其中会弹钢琴的人数比会弹古筝的人数多10人,两种都会的有7人.设会弹古筝的有m人,则该班同学共有人(用含m的代数式表示)17. 观察下列等式(式子中的“!”是一种数学运算符号)1! = 1,2! = 2×1,3! = 3×2×1,4! = 4×3×2×1,……,那么计算: = .18. 某学习小组由学生和教师组成,人员构成同时满足以下三个条件:a.男生人数多于女生人数;b.女生人数多于教师人数;c.教师人数的2倍多于男生人数.①若教师人数为4,则女生人数的最大值为 ②该小组人数的最小值为
三、解答题
-
19. 先化简,再求值: , 其中20. 已知关于 , 的二元一次方程组 的解满足 ,求 的取值范围.21. 如图所示,一次函数y=kx+b与反比例函数y= 的图象交于A(2,4),B(﹣4,n)两点.
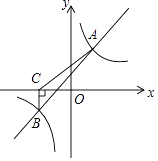 (1)、分别求出一次函数与反比例函数的表达式;(2)、过点B作BC⊥x轴,垂足为点C,连接AC,求△ACB的面积.22. 如图,在△ABC中,∠B=90°, ,D是 上的一点,连结 ,若∠BDC=60°,BD= .试求AC的长.
(1)、分别求出一次函数与反比例函数的表达式;(2)、过点B作BC⊥x轴,垂足为点C,连接AC,求△ACB的面积.22. 如图,在△ABC中,∠B=90°, ,D是 上的一点,连结 ,若∠BDC=60°,BD= .试求AC的长. 23. 为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,若两车合作,各运12趟才能完成,需支付运费共4 800元.若甲、乙两车单独运完此堆垃圾,则乙车所运趟数是甲车的2倍,已知乙车每趟运费比甲车少200元.(1)、分别求出甲、乙两车每趟的运费;(2)、若单独租用甲车运完此堆垃圾,需多少趟?(3)、若同时租用甲、乙两车,则甲车运x趟,乙车运y趟,才能运完此堆垃圾,其中x,y均为正整数.
23. 为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,若两车合作,各运12趟才能完成,需支付运费共4 800元.若甲、乙两车单独运完此堆垃圾,则乙车所运趟数是甲车的2倍,已知乙车每趟运费比甲车少200元.(1)、分别求出甲、乙两车每趟的运费;(2)、若单独租用甲车运完此堆垃圾,需多少趟?(3)、若同时租用甲、乙两车,则甲车运x趟,乙车运y趟,才能运完此堆垃圾,其中x,y均为正整数.①当x=10时,y=;当y=10时,x=;
②用含x的代数式表示y;
(4)、探究:
在(3)的条件下:①用含x的代数式表示总运费w;
②要想总运费不大于4 000元,甲车最多需运多少趟?