内蒙古扎鲁特旗、霍林郭勒市2019-2020学年九年级下学期数学6月月考试卷
试卷更新日期:2021-03-15 类型:月考试卷
一、单选题
-
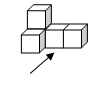
1. -4的绝对值是( )A、4 B、 C、-4 D、2. 下列运算中正确的是( )A、 B、 C、 D、3. 如图的几何体是由五个相同的小立方体搭成,它的左视图是( )
 A、
A、 B、
B、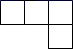 C、
C、 D、
D、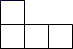 4.
4.下列图形:

任取一个是中心对称图形的概率是( )
A、 B、 C、 D、15. 若关于x的不等式组 有解,则实数a的取值范围是( )A、a >4 B、a< 4 C、 D、6. 在半径等于5 cm的圆内有长为 cm的弦,则此弦所对的圆周角为( )A、60° B、120° C、60°或120° D、30°或120°7. 学校为创建“书香校园”购买了一批图书.已知购买科普类图书花费10000元,购买文学类图书花费9000元,其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元,且购买科普书的数量比购买文学书的数量少100本.求科普类图书平均每本的价格是多少元?若设科普类图书平均每本的价格是x元,则可列方程为( )
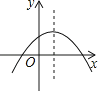
A、 ﹣ =100 B、 ﹣ =100 C、 ﹣ =100 D、 ﹣ =1008.二次函数y=ax2+bx+c的图象在平面直角坐标系中的位置如图所示,则一次函数y=ax+b与反比例函数在同一平面直角坐标系中的图象可能是( )
 A、
A、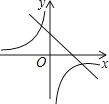 B、
B、 C、
C、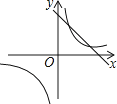 D、
D、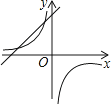 9. 如图,直线 , 交 于 两点, 分别是 的角平分线,则四边形ABCD是( )
9. 如图,直线 , 交 于 两点, 分别是 的角平分线,则四边形ABCD是( )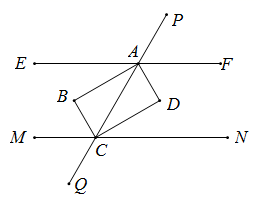 A、菱形 B、平行四边形 C、矩形 D、不能确定10. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b<m (am+b)(m≠1的实数).其中正确结论的有( )
A、菱形 B、平行四边形 C、矩形 D、不能确定10. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b<m (am+b)(m≠1的实数).其中正确结论的有( )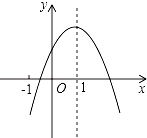 A、①②③ B、①③④ C、③④⑤ D、②③⑤
A、①②③ B、①③④ C、③④⑤ D、②③⑤二、填空题
-
11. 截止到2020年6月27日,全球新冠肺炎确诊总数累计超过978万例,用科学记数法可将978万表示为 .12. 若关于x的一元二次方程 有两个实数根,则k的取值范围为 .13. 一组数据2,x,1,3,5,4,若这组数据的中位数是3,则这组数据的方差是 .
14. 汽车产业的发展,有效促进我国现代化建设.某汽车销售公司2005年盈利1500万元,到2007年盈利2160万元,则这两年的年平均增长率是 .15. 如图,在半径为13的⊙O中,弦AB=10,点C是优弧 上一点(不与A,B重合),则cosC的值为 .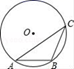 16. 如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C,若∠ACB=30°,AB= ,则阴影部分的面积是 .
16. 如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C,若∠ACB=30°,AB= ,则阴影部分的面积是 . 17. 观察下图(每幅图中最小的三角形都是全等的);则第n个图中这种最小的三角形共有个.
17. 观察下图(每幅图中最小的三角形都是全等的);则第n个图中这种最小的三角形共有个.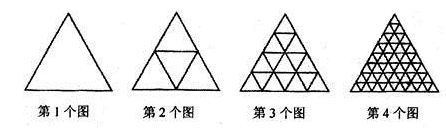
三、解答题
-
18. 计算: .19. 先化简,再求值: ,选一个你喜欢的数代入求值.20. 在一次数学活动课上,数学老师在同一平面内将一副直角三角板如图位置摆放,点C在 的延长线上, , , , , ,试求 的长.
 21. 在平面直角坐标系中,一次函数 (a≠0)的图象与反比例函数 的图象交于第二、第四象限内的A、B两点,与 轴交于点C,过点A作AH⊥ 轴,垂足为点H,OH=3,tan∠AOH= ,点B的坐标为( ,-2).
21. 在平面直角坐标系中,一次函数 (a≠0)的图象与反比例函数 的图象交于第二、第四象限内的A、B两点,与 轴交于点C,过点A作AH⊥ 轴,垂足为点H,OH=3,tan∠AOH= ,点B的坐标为( ,-2).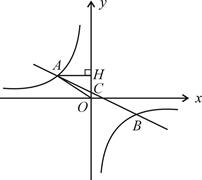 (1)、求该反比例函数和一次函数的解析式;(2)、求△AHO的周长.22. 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)、求该反比例函数和一次函数的解析式;(2)、求△AHO的周长.22. 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.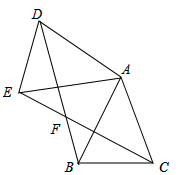 (1)、求证: ;(2)、若AB=2, ,当四边形ADFC是菱形时,求BF的长.23. 垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
(1)、求证: ;(2)、若AB=2, ,当四边形ADFC是菱形时,求BF的长.23. 垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.运动员甲测试成绩表
测试序号
1
2
3
4
5
6
7
8
9
10
成绩(分)
7
6
8
7
7
5
8
7
8
7

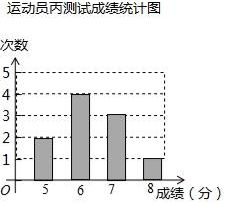 (1)、写出运动员甲测试成绩的众数为;运动员乙测试成绩的中位数为;运动员丙测试成绩的平均数为;(2)、经计算三人成绩的方差分别为S甲2=0.8、S乙2=0.4、S丙2=0.8,请综合分析,在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?(3)、甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)24. 如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)、写出运动员甲测试成绩的众数为;运动员乙测试成绩的中位数为;运动员丙测试成绩的平均数为;(2)、经计算三人成绩的方差分别为S甲2=0.8、S乙2=0.4、S丙2=0.8,请综合分析,在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?(3)、甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)24. 如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P. (1)、求证:PD是⊙O的切线;(2)、求证:△PBD∽△DCA;(3)、当AB=6,AC=8时,求线段PB的长.25. 某梁平特产专卖店销售“梁平柚”,已知“梁平柚”的进价为每个10元,现在的售价是每个16元,每天可卖出120个.市场调查反映:如调整价格,每涨价1元,每天要少卖出10个;每降价1元,每天可多卖出30个.(1)、如果专卖店每天要想获得770元的利润,且要尽可能的让利给顾客,那么售价应涨价多少元?(2)、请你帮专卖店老板算一算,如何定价才能使利润最大,并求出此时的最大利润?26. 如图所示,已知抛物线y=x2-1与x轴交于A、B两点,与y轴交于点C.
(1)、求证:PD是⊙O的切线;(2)、求证:△PBD∽△DCA;(3)、当AB=6,AC=8时,求线段PB的长.25. 某梁平特产专卖店销售“梁平柚”,已知“梁平柚”的进价为每个10元,现在的售价是每个16元,每天可卖出120个.市场调查反映:如调整价格,每涨价1元,每天要少卖出10个;每降价1元,每天可多卖出30个.(1)、如果专卖店每天要想获得770元的利润,且要尽可能的让利给顾客,那么售价应涨价多少元?(2)、请你帮专卖店老板算一算,如何定价才能使利润最大,并求出此时的最大利润?26. 如图所示,已知抛物线y=x2-1与x轴交于A、B两点,与y轴交于点C.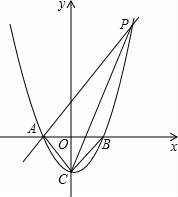 (1)、求A、B、C三点的坐标;(2)、过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积;(3)、在x轴上方的抛物线上是否存在一点M,过M作MG⊥x轴于点G,使以A、M、G三点为顶点的三角形与△PCA相似?若存在,请求出M点的坐标;否则,请说明理由.
(1)、求A、B、C三点的坐标;(2)、过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积;(3)、在x轴上方的抛物线上是否存在一点M,过M作MG⊥x轴于点G,使以A、M、G三点为顶点的三角形与△PCA相似?若存在,请求出M点的坐标;否则,请说明理由.