初中数学湘教版九年级下册3.1投影 同步练习
试卷更新日期:2021-03-14 类型:同步测试
一、单选题
-
1. 如图所示是一天中不同时刻直立的灯杆在阳光下形成的影长,规定各图向右为正东方向,将各图按时间顺序排列正确的是( )
 A、②④①③ B、①④③② C、②④③① D、①③②④2. 如图,水杯的杯口与投影面平行,投影线的几方向如箭头所示,它的正投影是( )
A、②④①③ B、①④③② C、②④③① D、①③②④2. 如图,水杯的杯口与投影面平行,投影线的几方向如箭头所示,它的正投影是( ) A、
A、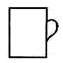 B、
B、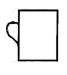 C、
C、 D、
D、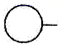 3. 如图是一棵小树一天内在太阳下不同时刻的照片,将它们按时间先后顺序进行排列正确的是( )
3. 如图是一棵小树一天内在太阳下不同时刻的照片,将它们按时间先后顺序进行排列正确的是( ) A、③—④—①—② B、②—①—④—③ C、④—①—②—③ D、④—①—③—②4. 下列投影现象属于平行投影的是( )A、手电筒发出的光线所形成的投影 B、太阳光发出的光线所形成的投影 C、路灯发出的光线所形成的投影 D、台灯发出的光线所形成的投影5. 小明在太阳光下观察矩形木板的影子,不可能是( )A、平行四边形 B、矩形 C、线段 D、梯形6. 下列光线所形成的投影不是中心投影的是( )A、太阳光线 B、台灯的光线 C、手电筒的光线 D、路灯的光线7. 如图,在直角坐标系中,点P(2,2)是一个光源.木杆AB两端的坐标分别为(0,1),(3,1).则木杆AB在x轴上的投影长为( )
A、③—④—①—② B、②—①—④—③ C、④—①—②—③ D、④—①—③—②4. 下列投影现象属于平行投影的是( )A、手电筒发出的光线所形成的投影 B、太阳光发出的光线所形成的投影 C、路灯发出的光线所形成的投影 D、台灯发出的光线所形成的投影5. 小明在太阳光下观察矩形木板的影子,不可能是( )A、平行四边形 B、矩形 C、线段 D、梯形6. 下列光线所形成的投影不是中心投影的是( )A、太阳光线 B、台灯的光线 C、手电筒的光线 D、路灯的光线7. 如图,在直角坐标系中,点P(2,2)是一个光源.木杆AB两端的坐标分别为(0,1),(3,1).则木杆AB在x轴上的投影长为( )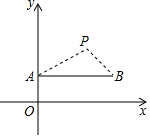 A、3 B、5 C、6 D、78. 某数学兴趣小组利用阳光下的影子测量建筑物的高度,已知小明的身高1.5m,测量其影子为1.2m,建筑物的影长为14m,则建筑物的高是( )m.A、16.5 B、17 C、17.5 D、189. 在同一时刻的阳光下,身高1.6 m的小强的影长是1.2 m,旗杆的影长是15 m,则旗杆的高为( )A、16 m B、18 m C、20 m D、22 m10. 如图,在离某围端 的6米处有一棵树 ,在某时刻2米长的竹竿垂直地面,太阳光下的影长为3米,此时,树的影子有一部分映在地面上,还有一部分影子映在墙上 处,墙上的影高为4米,那么这棵树高约为( )
A、3 B、5 C、6 D、78. 某数学兴趣小组利用阳光下的影子测量建筑物的高度,已知小明的身高1.5m,测量其影子为1.2m,建筑物的影长为14m,则建筑物的高是( )m.A、16.5 B、17 C、17.5 D、189. 在同一时刻的阳光下,身高1.6 m的小强的影长是1.2 m,旗杆的影长是15 m,则旗杆的高为( )A、16 m B、18 m C、20 m D、22 m10. 如图,在离某围端 的6米处有一棵树 ,在某时刻2米长的竹竿垂直地面,太阳光下的影长为3米,此时,树的影子有一部分映在地面上,还有一部分影子映在墙上 处,墙上的影高为4米,那么这棵树高约为( ) A、6 B、8 C、9 D、10
A、6 B、8 C、9 D、10二、填空题
-
11. 一天下午,小红先参加了校运动会女子 比赛,然后又参加了女子 比赛,摄影师在同一位置拍摄了她参加这两场比赛的照片如图所示,则小红参加 比赛的照片是.(填“图1”或“图2”)
 12. 地面上有一支蜡烛,蜡烛前面有一面墙,王涛同学在蜡烛与墙之间运动,则他在墙上的投影长度随着他离墙的距离变小而(增大、变小)13. 在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.5m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ的长度为m.
12. 地面上有一支蜡烛,蜡烛前面有一面墙,王涛同学在蜡烛与墙之间运动,则他在墙上的投影长度随着他离墙的距离变小而(增大、变小)13. 在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.5m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ的长度为m.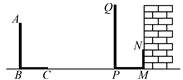 14. 墙壁CD上D处有一盏灯(如图),小明站在A处测得他的影长与身长相等,都为1.6m,他向墙壁走1m到B处时发现影子刚好落在A点,则灯泡与地面的距离CD= .
14. 墙壁CD上D处有一盏灯(如图),小明站在A处测得他的影长与身长相等,都为1.6m,他向墙壁走1m到B处时发现影子刚好落在A点,则灯泡与地面的距离CD= . 15. 《孙子算经》是我国古代重要的数学著作,成书于约一千五百年前,其中有道歌谣算题:“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问杆长几何?”歌谣的意思是:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五,同时立一根一尺五的小标杆,它的影长五寸(提示:仗和尺是古代的长度单位,1丈=10尺,1尺=10寸),可以求出竹竿的长为尺.
15. 《孙子算经》是我国古代重要的数学著作,成书于约一千五百年前,其中有道歌谣算题:“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问杆长几何?”歌谣的意思是:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五,同时立一根一尺五的小标杆,它的影长五寸(提示:仗和尺是古代的长度单位,1丈=10尺,1尺=10寸),可以求出竹竿的长为尺.三、解答题
-
16. 如图,两幢楼高AB=CD=30m,两楼间的距离AC=24m,当太阳光线与水平线的夹角为30°时,求甲楼投在乙楼上的影子的高度.(结果精确到0.01, ≈1.732, ≈1.414)
 17. 已知一纸板的形状为正方形ABCD如图所示.其边长为10厘米,AD、BC与投影面β平行,AB、CD与投影面不平行,正方形在投影面β上的正投影为A1B1C1D1.若∠ABB1=45°,求投影面A1B1C1D1的面积.
17. 已知一纸板的形状为正方形ABCD如图所示.其边长为10厘米,AD、BC与投影面β平行,AB、CD与投影面不平行,正方形在投影面β上的正投影为A1B1C1D1.若∠ABB1=45°,求投影面A1B1C1D1的面积. 18. 某地夏季中午,当太阳移到屋顶上方偏南时,光线与地面成 角,房屋向南的窗户 高 米,现要在窗子外面的上方安装一个水平遮阳蓬 (如图所示).
18. 某地夏季中午,当太阳移到屋顶上方偏南时,光线与地面成 角,房屋向南的窗户 高 米,现要在窗子外面的上方安装一个水平遮阳蓬 (如图所示).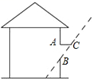 (1)、当遮阳蓬 的宽度在什么范围时,太阳光线能射入室内?(2)、当遮阳蓬 的宽度在什么范围时,太阳光线不能射入室内?19. 学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为 的小明 的影子 长是 ,而小颖 刚好在路灯灯泡的正下方 点,并测得 .
(1)、当遮阳蓬 的宽度在什么范围时,太阳光线能射入室内?(2)、当遮阳蓬 的宽度在什么范围时,太阳光线不能射入室内?19. 学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为 的小明 的影子 长是 ,而小颖 刚好在路灯灯泡的正下方 点,并测得 . (1)、请在图中画出形成影子的光线,并确定路灯灯泡所在的位置 ;(2)、求路灯灯泡的垂直高度 ;(3)、如果小明沿线段BH向小颖(点H)走去,当小明走到BH中点B1处时,请在图中画出此时小明的影长B1C1 , 并求B1C1的长;
(1)、请在图中画出形成影子的光线,并确定路灯灯泡所在的位置 ;(2)、求路灯灯泡的垂直高度 ;(3)、如果小明沿线段BH向小颖(点H)走去,当小明走到BH中点B1处时,请在图中画出此时小明的影长B1C1 , 并求B1C1的长;