初中数学湘教版九年级下册第二章圆章末检测（提高练）

试卷更新日期：2021-03-14 类型：单元试卷

进入出卷网下载

一、单选题

1. 若 $R t △ A B C$ 的外接圆半径为R，内切圆半径为 $r$ ，则其内切圆的面积与 $R t △ A B C$ 的面积比为（）

A、 $\frac{π r}{2 r + 2 R}$ B、 $\frac{π r}{2 R + r}$ C、 $\frac{π r}{4 R + 2 r}$ D、 $\frac{π r}{4 R + r}$

查看试题解析
2. 如图，点A，B，C均在坐标轴上，AO=BO=CO=1，过A，O，C作⊙D，E是⊙D上任意一点，连结CE， BE，则 $C E^{2} + B E^{2}$ 的最大值是（）

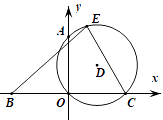A、4 B、5 C、6 D、 $4 + \sqrt{2}$

查看试题解析
3. 如图，AB是⊙O的直径，点D，C在⊙O上，∠DOC＝90°，AD＝ $\sqrt{2}$ ，BC＝1，则⊙O的半径为（）

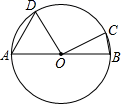A、 $\sqrt{3}$ B、 $\frac{\sqrt{5}}{2}$ C、 $\frac{\sqrt{10}}{2}$ D、 $\frac{\sqrt{2} + 1}{2}$

查看试题解析
4. 如图，AC，BC是两个半圆的直径，∠ACP=30°，若AB=2a，则 PQ的值为（）

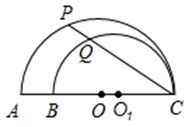A、a B、1.5a C、 $\sqrt{3} a$ D、 $2 \sqrt{3} a$

查看试题解析
5. 如图，A，B，C是⊙O上三个点，∠AOB=2∠BOC，则下列说法中正确的是（）

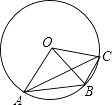A、∠OBA=∠OCA B、四边形OABC内接于⊙O C、AB=2BC D、∠OBA+∠BOC=90°

查看试题解析
6. 如图，直线y＝ $\frac{\sqrt{3}}{3}$ x＋ $\sqrt{3}$ 与x轴、y轴分别相交于A、B两点，圆心P的坐标为（1，0），⊙P与y轴相切于点O．若将⊙P沿x轴向左移动，当⊙P与该直线相交时，满足横坐标为整数的点P的个数是（）

A、3 B、4 C、5 D、6

查看试题解析
7. 如图，已知直线l的函数表达式为 $y = \frac{3}{4} x + 3$ ，它与x轴、y轴的交点分别为 $A 、 B$ 两点．

(1)、若 $⊙ O$ 的半径为2，说明直线 $A B$ 与 $⊙ O$ 的位置关系；

(2)、若 $⊙ P$ 的半径为2， $⊙ P$ 经过点B且与x轴相切于点F，求圆心P的坐标；

(3)、若 $Δ A B O$ 的内切圆圆心是点M，外接圆圆心是点N，请直接写出 $M N$ 的长度．

查看试题解析
8. 在平面直角坐标系 $x O y$ 中，直线经过点A（－3，0），点B（0， $\sqrt{3}$ ），点P的坐标为（1，0），与 $y$ 轴相切于点O，若将⊙P沿 $x$ 轴向左平移，平移后得到（点P的对应点为点P′），当⊙P′与直线相交时，横坐标为整数的点P′共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 在 Rt△ABC ，∠C=90°，AB=6．△ABC的内切圆半径为1，则△ABC的周长为（）

A、13 B、14 C、15 D、16

查看试题解析
10. 若四边形A鱿O的对角线AC，BD相交于O，△AOB，△BOC，△COD，△DOA的周长相等，且△AOB，△BOC，△COD的内切圆半径分别为3，4，6，则△DOA的内切圆半径是（ )

A、 $\frac{9}{2}$ B、 $\frac{3}{2}$ C、 $\frac{7}{2}$ D、以上答案均不正确

查看试题解析
11. 如图，王虎使一长为4cm，宽为3cm的长方形木板，在桌面上做无滑动的翻滚（顺时针方向）木板上点A位置变化为A→A₁→A₂ ，其中第二次翻滚被桌面上一小木块挡住，使木板与桌面成30°角，则点A翻滚到A₂位置时共走过的路径长为（）

A、10cm B、4πcm C、 $\frac{7}{2} π cm$ D、 $\frac{5}{2} cm$

查看试题解析
12. 已知正方形MNOK和正六边形ABCDEF边长均为1，把正方形放在正六边形中，使OK边与AB边重合，如图所示．按下列步骤操作：将正方形在正六边形中绕点B顺时针旋转，使KM边与BC边重合，完成第一次旋转；再绕点C顺时针旋转，使MN边与CD边重合，完成第二次旋转；……在这样连续6次旋转的过程中，点B ， M间的距离不可能是（）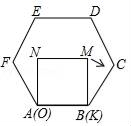

A、0.5 B、0.6 C、0.7 D、0.8

查看试题解析

二、填空题

13. 如图，在平面直角坐标系中， $A (0 ， 4) 、 B (4 ， 4) 、 C (6 ， 2)$ ，则经过 $A 、 B 、 C$ 三点的圆弧所在圆的圆心M的坐标为；点D坐标为 $(8 ， - 2)$ ，连接 $C D$ ，直线 $C D$ 与 $⊙ M$ 的位置关系是．

查看试题解析
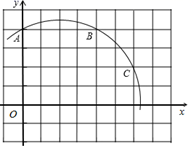14. 如图，AB为⊙O的直径，C为⊙O上一点，其中AB＝2，∠AOC＝120°，P为⊙O上的动点，连AP，取AP中点Q，连CQ，则线段CQ的最大值为.

查看试题解析
15. 如图，直线 $y = - \frac{3}{4} x + 3$ 与x轴、y轴分别交于点A、B；点Q是以C（0，﹣1）为圆心、1为半径的圆上一动点，过Q点的切线交线段AB于点P，则线段PQ的最小是．

查看试题解析
16. 如图1是小明制作的一副弓箭，点A，D分别是弓臂BAC与弓弦BC的中点，弓弦BC＝60cm.沿AD方向拉动弓弦的过程中，假设弓臂BAC始终保持圆弧形，弓弦不伸长.如图2，当弓箭从自然状态的点D拉到点D₁时，有AD₁＝30cm，∠B₁D₁C₁＝120°.

(1)、图2中，弓臂两端B₁ ， C₁的距离为cm.

(2)、如图3，将弓箭继续拉到点D₂ ，使弓臂B₂AC₂为半圆，则D₁D₂的长为cm.

查看试题解析
17. 如图，∠AOB=45°，点P、Q都在射线OA上，OP=2，OQ=6.M是射线OB上的一个动点，过P、Q、M三点作圆，当该圆与OB相切时，其半径的长为.

查看试题解析
18. 如图，正六边形 $A_{1} A_{2} A_{3} A_{4} A_{5} A_{6}$ 内部有一个正五形 $B_{1} B_{2} B_{3} B_{4} B_{5}$ ，且 $A_{3} A_{4} // B_{3} B_{4}$ ，直线 $l$ 经过 $B_{2}$ 、 $B_{3}$ ，则直线 $l$ 与 $A_{1} A_{2}$ 的夹角 $α =$ $^{°}$ .

查看试题解析

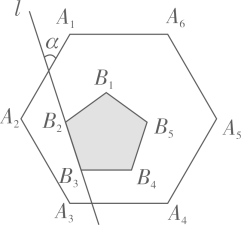
三、综合题

19. 问题：我们知道，过任意的一个三角形的三个顶点能作一个圆，这个圆叫做三角形的外接圆.
那么任意的一个四边形有外接圆吗？

(1)、探索：如图给出了一些四边形，填写出你认为有外接圆的图形序号.

(2)、发现：相对的内角之和满足什么关系时，四边形一定有外接圆，写出你的发现：.

(3)、说理：如果四边形没有外接圆，那么相对的两个内角之和有上面的关系吗？请结合图④，说明理由.

查看试题解析
20. 已知四边形ABCD的四个顶点都在⊙O上，对角线AC和BD交于点E．

(1)、若∠BAD和∠BCD的度数之比为1：2，求∠BCD的度数；

(2)、若AB＝3，AD＝5，∠BAD＝60°，点C为劣弧BD的中点，求弦AC的长；

(3)、若⊙O的半径为1，AC+BD＝3，且AC⊥BD．求线段OE的取值范围．

查看试题解析
21. 车辆转弯时，能否顺利通过直角弯道的标准是：车辆是否可以行使到和路的边界夹角是45°的位置(如图1中②的位置)，例如，图2是某巷子的俯视图，巷子路面宽4m，转弯处为直角，车辆的车身为矩形ABCD，CD与DE、CE的夹角都是45°时，连接EF，交CD于点G，若GF的长度至少能达到车身宽度，则车辆就能通过.

(1)、试说明长8m，宽3m的消防车不能通过该直角转弯；

(2)、为了能使长8m，宽3m的消防车通过该弯道，可以将转弯处改为圆弧(分别是以O为圆心，以OM和ON为半径的弧)，具体方案如图3，其中OM⊥OM′，请你求出ON的最小值.

查看试题解析
22. 问题提出

(1)、如图①，在△ABC中，∠A＝120°，AB＝AC＝5，则△ABC的外接圆半径R的值为．
问题探究

(2)、如图②，⊙O的半径为13，弦AB＝24，M是AB的中点，P是⊙O上一动点，求PM的最大值．
问题解决

(3)、如图③所示，AB、AC、 $\overset{⌢}{B C}$ 是某新区的三条规划路，其中AB＝6km ， AC＝3km ， ∠BAC＝60°， $\overset{⌢}{B C}$ 所对的圆心角为60°，新区管委会想在 $\overset{⌢}{B C}$ 路边建物资总站点P ，在AB ， AC路边分别建物资分站点E、F ，也就是，分别在 $\overset{⌢}{B C}$ 、线段AB和AC上选取点P、E、F ．由于总站工作人员每天都要将物资在各物资站点间按P→E→F→P的路径进行运输，因此，要在各物资站点之间规划道路PE、EF和FP ．为了快捷、环保和节约成本．要使得线段PE、EF、FP之和最短，试求PE+EF+FP的最小值．（各物资站点与所在道路之间的距离、路宽均忽略不计）

查看试题解析
23. 阅读以下材料，并按要求完成相应地任务：
莱昂哈德·欧拉(Leonhard Euler)是瑞士数学家，在数学上经常见到以他的名字命名的重要常数，公式和定理，下面是欧拉发现的一个定理：在△ABC中，R和r分别为外接圆和内切圆的半径，O和I分别为其外心和内心，则 $O I^{2} = R^{2} - 2 R r$ .

如图1，⊙O和⊙I分别是△ABC的外接圆和内切圆，⊙I与AB相切分于点F，设⊙O的半径为R，⊙I的半径为r，外心O（三角形三边垂直平分线的交点）与内心I（三角形三条角平分线的交点）之间的距离OI＝d，则有d²＝R²﹣2Rr．

下面是该定理的证明过程（部分）：

延长AI交⊙O于点D，过点I作⊙O的直径MN，连接DM，AN.

∵∠D=∠N，∠DMI=∠NAI(同弧所对的圆周角相等)，

∴△MDI∽△ANI，

∴ $\frac{I M}{I A} = \frac{I D}{I N}$ ，

∴ $I A \cdot I D = I M \cdot I N$ ①，

如图2，在图1(隐去MD，AN)的基础上作⊙O的直径DE，连接BE，BD，BI，IF，

∵DE是⊙O的直径，∴∠DBE=90°，

∵⊙I与AB相切于点F，∴∠AFI=90°，

∴∠DBE=∠IFA，

∵∠BAD=∠E(同弧所对圆周角相等)，

∴△AIF∽△EDB，

∴ $\frac{I A}{D E} = \frac{I F}{B D}$ ，∴ $I A \cdot B D = D E \cdot I F$ ②，

任务：

(1)、观察发现： $I M = R + d$ ， $I N =$ (用含R，d的代数式表示)；

(2)、请判断BD和ID的数量关系，并说明理由；

(3)、请观察式子①和式子②，并利用任务(1)，(2)的结论，按照上面的证明思路，完成该定理证明的剩余部分；

(4)、应用：若△ABC的外接圆的半径为5cm，内切圆的半径为2cm，则△ABC的外心与内心之间的距离为cm.

查看试题解析
24. 阅读下列材料，然后解答问题．
经过正四边形(即正方形)各顶点的圆叫做这个正四边形的外接圆，圆心是正四边形的对称中心，这个正四边形叫做这个圆的内接正四边形．

如图，正方形ABCD内接于⊙O，⊙O的面积为S₁ ，正方形ABCD的面积为S₂ ．以圆心O为顶点作∠MON，使∠MON＝90°．将∠MON绕点O旋转，OM、ON分别与⊙O交于点E、F，分别与正方形ABCD的边交于点G、H．设由OE、OF、 $\overset{⌢}{E F}$ 及正方形ABCD的边围成的图形(阴影部分)的面积为S．

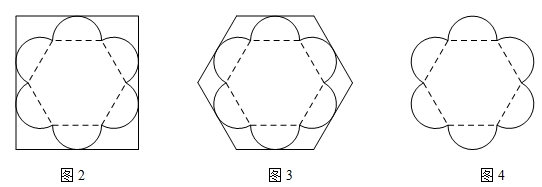
(1)、当OM经过点A时(如图①)，则S、S₁、S₂之间的关系为：(用含S₁、S₂的代数式表示)；

(2)、当OM⊥AB于G时(如图②)，则(1)中的结论仍然成立吗？请说明理由；

(3)、当∠MON旋转到任意位置时（如图③），则（1）中的结论任然成立吗：请说明理由.

查看试题解析
25. 已知某种月饼形状的俯视图如图1所示，该形状由1个正六边形和6个半圆组成，半圆直径与正六边形的边长相等.

现商家设计了2种棱柱体包装盒，其底面分别为矩形和正六边形(如图2和图3)我们可从底面的利用率来记算整个包装盒的利用情况.(底面利用率= $\frac{月饼面积}{包装盒底面面积}$ ×100%)

(1)、请分别计算出图2与图3中的底面利用率(结果保留到0.1%)；

(2)、考虑到节约成本，商家希望底面利用率能够不低于80%，且底面图形仍然采用最基本的几何形状，请问商家的要求是否能够满足，若可以满足，请设计一种方案，并直接写出此时的利用率；若不能满足，请说明理由.

查看试题解析
26. 如图，在 $Rt △ A B C$ 中， $∠ A C B = 90^{°}$ $A C = 6 ， B C = 8$ ，动点 $P$ 沿线段 $C B$ 从点 $C$ 向点 $B$ 运动，当点 $P$ 与点 $B$ 重合时，停止运动，以点 $P$ 为圆心， $P C$ 为半径作 $⊙ P$ ，点 $M$ 在 $⊙ P$ 上且在 $△ A B C$ 外， $∠ C P M = 90^{°}$ ．

(1)、当 $C P = 2 \sqrt{3}$ 时 $A P =$ ，点 $A$ 到 $⊙ P$ 的最远距离为；

(2)、 $⊙ P$ 与 $A B$ 相切于点 $D$ 时（如图2），求 $P C$ 的长？并求出此时劣弧 $\overset{⌢}{C D}$ 长度？（参考数据： $\sin 37^{°} = \frac{3}{5} ， \tan 37^{°} = \frac{3}{4}$ ）

(3)、直接写出点 $M$ 的运动路径长为， $B M$ 的最短距离为．

查看试题解析

初中数学湘教版九年级下册第二章 圆 章末检测（提高练）

一、单选题

二、填空题

三、综合题

初中数学湘教版九年级下册第二章圆章末检测（提高练）