初中数学湘教版九年级下册第二章 圆 章末检测(基础练)
试卷更新日期:2021-03-14 类型:单元试卷
一、单选题
-
1. 给出下列命题:
①弦是直径;②圆上两点间的距离叫弧;③长度相等的两段弧是等弧;④圆心角的度数与它所对的弧的度数相等;⑤圆是轴对称图形,不是中心对称图形;⑥直径是弦.其中正确的个数为( )
A、1 B、2 C、3 D、42. 如图,AB为⊙O的直径,点C在⊙O上,若∠ACO=50°,则∠B的度数为( ) A、60° B、50° C、40° D、30°3. 下列说法,正确的是( )A、等弦所对的圆周角相等 B、弦所对的两条弧的中点的连线垂直平分弦,且过圆心 C、切线垂直于圆的半径 D、平分弦的直径垂直于弦4. 如图,在⊙O中,点B是 的中点,点 在 上,连接 、 、 、 .若 ,则 的大小为( )
A、60° B、50° C、40° D、30°3. 下列说法,正确的是( )A、等弦所对的圆周角相等 B、弦所对的两条弧的中点的连线垂直平分弦,且过圆心 C、切线垂直于圆的半径 D、平分弦的直径垂直于弦4. 如图,在⊙O中,点B是 的中点,点 在 上,连接 、 、 、 .若 ,则 的大小为( )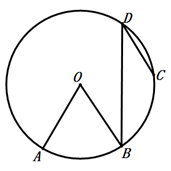 A、50° B、350° C、25° D、150°5. 如图,⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4,则AC的长等于( )
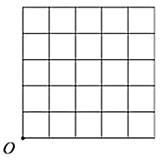
A、50° B、350° C、25° D、150°5. 如图,⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4,则AC的长等于( )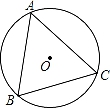 A、4 B、6 C、2 D、86. 如图,在5x5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
A、4 B、6 C、2 D、86. 如图,在5x5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )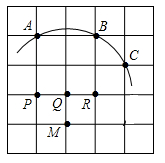 A、点P B、点Q C、点R D、点M7. 圆O的半径为3,圆心O到直线的距离为4,则该直线与圆O的位置关系是( )A、相切 B、相交 C、相离 D、以上都不对8. 如图,A为⊙O外一点,AB与⊙O相切于B点,点P是⊙O上的一个动点,若OB=5,AB=12,则AP的最小值为( )
A、点P B、点Q C、点R D、点M7. 圆O的半径为3,圆心O到直线的距离为4,则该直线与圆O的位置关系是( )A、相切 B、相交 C、相离 D、以上都不对8. 如图,A为⊙O外一点,AB与⊙O相切于B点,点P是⊙O上的一个动点,若OB=5,AB=12,则AP的最小值为( )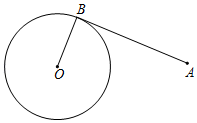 A、5 B、8 C、13 D、189. 如图,PA,PB分别切⊙O于点A,B,PA=12,CD切⊙O于点E,交PA,PB于点C,D两点,则△PCD的周长是( )
A、5 B、8 C、13 D、189. 如图,PA,PB分别切⊙O于点A,B,PA=12,CD切⊙O于点E,交PA,PB于点C,D两点,则△PCD的周长是( ) A、12 B、18 C、24 D、3010. 如图,点O是△ABC的内心,若∠A=70°,则∠BOC的度数是( )
A、12 B、18 C、24 D、3010. 如图,点O是△ABC的内心,若∠A=70°,则∠BOC的度数是( )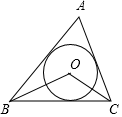 A、120° B、125° C、130° D、135°11. 如图,一块含有30°角的直角三角形ABC,在水平桌面上绕点C按顺时针方向旋转到A'、B'、C的位置。若BC的长为7.5cm,那么顶点A从开始到结束所经过的路径长为( )
A、120° B、125° C、130° D、135°11. 如图,一块含有30°角的直角三角形ABC,在水平桌面上绕点C按顺时针方向旋转到A'、B'、C的位置。若BC的长为7.5cm,那么顶点A从开始到结束所经过的路径长为( )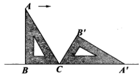 A、10πcm B、10 πcm C、15πcm D、20π12. 圆内接正六边形的边长与该边所对的劣弧的长的比是( )A、1: B、1:π C、3:π D、6:π
A、10πcm B、10 πcm C、15πcm D、20π12. 圆内接正六边形的边长与该边所对的劣弧的长的比是( )A、1: B、1:π C、3:π D、6:π二、填空题
-
13. 如图,在 的正方形网格中,两条网格线的交点叫做格点,每个小正方形的边长均为1.以点 为圆心,5为半径画圆,共经过图中个格点(包括图中网格边界上的点).
 14. 如下图,⊙O是△ABC的外接圆,若AB=OA=OB,则∠C等于°.
14. 如下图,⊙O是△ABC的外接圆,若AB=OA=OB,则∠C等于°.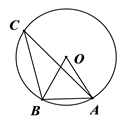 15. 赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的直径=米.
15. 赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的直径=米. 16. 如图,∠MON=45°,一直角三角尺△ABC的两个顶点C、A分别在OM,ON上移动,若AC=8,则点O到AC距离的最大值为.
16. 如图,∠MON=45°,一直角三角尺△ABC的两个顶点C、A分别在OM,ON上移动,若AC=8,则点O到AC距离的最大值为. 17. 如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,需添加的条件是 . (不添加其他字母和线条)
17. 如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,需添加的条件是 . (不添加其他字母和线条) 18. 如图,⊙O的半径为1,作两条互相垂直的直径AB、CD,弦AC是⊙O的内接正四边形的一条边.若以A为圆心,以1为半径画弧,交⊙O于点E,F,连接AE、CE,弦EC是该圆内接正n边形的一边,则该正n边形的面积为.
18. 如图,⊙O的半径为1,作两条互相垂直的直径AB、CD,弦AC是⊙O的内接正四边形的一条边.若以A为圆心,以1为半径画弧,交⊙O于点E,F,连接AE、CE,弦EC是该圆内接正n边形的一边,则该正n边形的面积为.
三、解答题
-
19. 如图,四边形ABCD内接于圆,AD、BC的延长线交于点E,F是BD延长线上一点,DE平分∠CDF.求证:AB=AC.
 20. 在南部沿海某气象站A测得一热带风暴从A的南偏东30°的方向迎着气象站袭来,已知该风暴速度为每小时20千米,风暴周围50千米范围内将受到影响,若该风暴不改变速度与方向,问气象站正南方60千米处的沿海城市B是否会受这次风暴的影响?若不受影响,请说明理由;若受影响,请求出受影响的时间.
20. 在南部沿海某气象站A测得一热带风暴从A的南偏东30°的方向迎着气象站袭来,已知该风暴速度为每小时20千米,风暴周围50千米范围内将受到影响,若该风暴不改变速度与方向,问气象站正南方60千米处的沿海城市B是否会受这次风暴的影响?若不受影响,请说明理由;若受影响,请求出受影响的时间.
21. 在附中中心花园的草坪上,有一些自动旋转喷泉水装置,它的喷灌区域是一个扇形,小孙同学想了解这种装置能够喷灌的草坪面积,他测量岀了相关数据,并画出了示意图.如图,这种旋转喷水装置的旋转角度为240°,喷灌起终点A,B两点的距离为12米,求这种装置能够喷灌的草坪面积.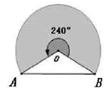 22. 如图,破残的圆形轮片上,弦AB的垂直平分线交AB于C,交弦AB于D.
22. 如图,破残的圆形轮片上,弦AB的垂直平分线交AB于C,交弦AB于D. (1)、求作此残片所在的圆(不写作法,保留作图痕迹);(2)、若AB=24cm,CD=8cm,求(1)中所作圆的半径.23. 如图所示,线段AB=1.8cm,作满足下面要求的图形.
(1)、求作此残片所在的圆(不写作法,保留作图痕迹);(2)、若AB=24cm,CD=8cm,求(1)中所作圆的半径.23. 如图所示,线段AB=1.8cm,作满足下面要求的图形. (1)、到点A和点B的距离都小于1.1cm的所有点组成的图形.(2)、到点A和点B距离都大于1.1cm的所有点组成的图形.24. “筒车”是一种以水流作动力,取水灌田的工具。据史料记载,它发明于隋而盛于唐,距今已有1000多年的历史,是我国古代劳动人民的一项伟大创造. 明朝科学家徐光启在《农政全书》中用图画描绘了“筒车”的工作原理. 如图,“筒车”盛水筒的运行轨迹是以轴心 为圆心的圆,已知圆心 在水面上方,且当圆被水面截得的弦 为6米时,水面下盛水筒的最大深度为1米(即水面下方部分圆上一点距离水面的最大距离).
(1)、到点A和点B的距离都小于1.1cm的所有点组成的图形.(2)、到点A和点B距离都大于1.1cm的所有点组成的图形.24. “筒车”是一种以水流作动力,取水灌田的工具。据史料记载,它发明于隋而盛于唐,距今已有1000多年的历史,是我国古代劳动人民的一项伟大创造. 明朝科学家徐光启在《农政全书》中用图画描绘了“筒车”的工作原理. 如图,“筒车”盛水筒的运行轨迹是以轴心 为圆心的圆,已知圆心 在水面上方,且当圆被水面截得的弦 为6米时,水面下盛水筒的最大深度为1米(即水面下方部分圆上一点距离水面的最大距离).
 (1)、求该圆的半径;(2)、若水面上涨导致圆被水面截得的弦 从原来的6米变为8米时,则水面上涨的高度为多少米?25. 在△ABC中,∠C= ,⊙O是△ABC的内切圆,⊙P分别与CA的延长线、CB的延长线以及直线AB均相切,⊙O的半径为m,⊙P的半径为n.
(1)、求该圆的半径;(2)、若水面上涨导致圆被水面截得的弦 从原来的6米变为8米时,则水面上涨的高度为多少米?25. 在△ABC中,∠C= ,⊙O是△ABC的内切圆,⊙P分别与CA的延长线、CB的延长线以及直线AB均相切,⊙O的半径为m,⊙P的半径为n.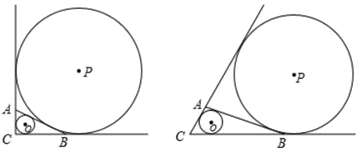 (1)、当 =90°时,AC=6,BC=8时,m= , n=.(2)、当 取下列度数时,求△ABC的面积(用含有m、n的代数式表示,并直接写出答案).①如图, =90°;②如图, =60°.26. 我们知道,与三角形各边都相切的圆叫做三角形的内切圆,则三角形可以称为圆的外切三角形.如图1, 与 的三边 分别相切于点 则 叫做 的外切三角形.以此类推,各边都和圆相切的四边形称为圆外切四边形.如图2, 与四边形ABCD的边 分别相切于点 则四边形 叫做 的外切四边形.
(1)、当 =90°时,AC=6,BC=8时,m= , n=.(2)、当 取下列度数时,求△ABC的面积(用含有m、n的代数式表示,并直接写出答案).①如图, =90°;②如图, =60°.26. 我们知道,与三角形各边都相切的圆叫做三角形的内切圆,则三角形可以称为圆的外切三角形.如图1, 与 的三边 分别相切于点 则 叫做 的外切三角形.以此类推,各边都和圆相切的四边形称为圆外切四边形.如图2, 与四边形ABCD的边 分别相切于点 则四边形 叫做 的外切四边形.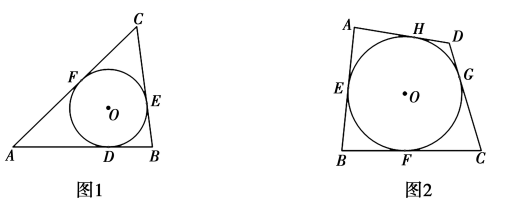 (1)、如图2,试探究圆外切四边形 的两组对边 与 之间的数量关系,猜想: (横线上填“>”,“<”或“=”);(2)、利用图2证明你的猜想(写出已知,求证,证明过程);(3)、用文字叙述上面证明的结论:;(4)、若圆外切四边形的周长为 相邻的三条边的比为 ,求此四边形各边的长.
(1)、如图2,试探究圆外切四边形 的两组对边 与 之间的数量关系,猜想: (横线上填“>”,“<”或“=”);(2)、利用图2证明你的猜想(写出已知,求证,证明过程);(3)、用文字叙述上面证明的结论:;(4)、若圆外切四边形的周长为 相邻的三条边的比为 ,求此四边形各边的长.