初中数学湘教版九年级下册2.6弧长与扇形面积 同步练习
试卷更新日期:2021-03-14 类型:同步测试
一、单选题
-
1. 若扇形的半径为3,圆心角为60°,则此扇形的弧长是( )A、π B、 2π C、 3π D、4π2. 如图,AB为⊙O的直径,点C在⊙O上,若 , ,则 的长为( )
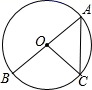 A、 B、 C、 D、3. 如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A,B,与⊙O1分别交于C,D,则 与 的弧长之和为( )
A、 B、 C、 D、3. 如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A,B,与⊙O1分别交于C,D,则 与 的弧长之和为( )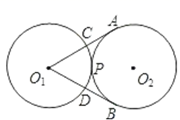 A、 B、 C、 D、4. 计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.下面是同一个任务进行到不同阶段时进度条的示意图:
A、 B、 C、 D、4. 计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.下面是同一个任务进行到不同阶段时进度条的示意图: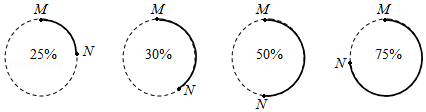
若圆半径为1,当任务完成的百分比为x时,线段MN的长度记为d(x).下列描述正确的是( )
A、d(25%)=1 B、当x>50%时,d(x)>1 C、当x1>x2时,d(x1)>d(x2) D、当x1+x2=100%时,d(x1)=d(x2)5. 如图,由六段相等的圆弧组成的三叶花,每段圆弧都是四分之一圆周,OA=OB=OC=2,则这朵三叶花的面积为( )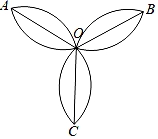 A、3π﹣3 B、3π﹣6 C、6π﹣3 D、6π﹣66. 如图,已知扇形的圆心角为60°,半径为3,则图中弓形(阴影部分)的面积为( )
A、3π﹣3 B、3π﹣6 C、6π﹣3 D、6π﹣66. 如图,已知扇形的圆心角为60°,半径为3,则图中弓形(阴影部分)的面积为( ) A、6π﹣9 B、6π﹣3 C、 D、7. 如图,在由边长为1的小正方形组成的网格中,点A,B,C,D都在格点上,点E在AB的延长线上,以A为圆心,AE为半径画弧,交AD的延长线于点F,且弧EF经过点C,则 的长为( )
A、6π﹣9 B、6π﹣3 C、 D、7. 如图,在由边长为1的小正方形组成的网格中,点A,B,C,D都在格点上,点E在AB的延长线上,以A为圆心,AE为半径画弧,交AD的延长线于点F,且弧EF经过点C,则 的长为( ) A、 B、 C、 D、8. 已知圆锥的母线长为6,将其侧面沿着一条母线展开,所得扇形的圆心角为120°,则该扇形面积是( ).A、4π B、8π C、12π D、16π9. 用一个半径为3,面积为6π的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径为( )A、π B、2π C、2 D、110. 如图, 的三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将 绕点B顺时针旋转到 的位置,且点 、 仍落在格点上,则线段 扫过的图形的面积是( )平方单位(结果保留)
A、 B、 C、 D、8. 已知圆锥的母线长为6,将其侧面沿着一条母线展开,所得扇形的圆心角为120°,则该扇形面积是( ).A、4π B、8π C、12π D、16π9. 用一个半径为3,面积为6π的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径为( )A、π B、2π C、2 D、110. 如图, 的三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将 绕点B顺时针旋转到 的位置,且点 、 仍落在格点上,则线段 扫过的图形的面积是( )平方单位(结果保留) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,小明从纸上剪下一个圆形和一个扇形纸片,用它们恰好能围成一个圆锥模型.若圆的半径为1,扇形的圆心角为120°,则此扇形的半径为.
 12. 一种圆角正方形桌面如图所示.每段圆弧所对的圆心角是90°,用一根直尺测得轮廓上两点之间距离的最大值是 ,平行的两直边之间的距离为 ,则该圆角正方形的周长是.
12. 一种圆角正方形桌面如图所示.每段圆弧所对的圆心角是90°,用一根直尺测得轮廓上两点之间距离的最大值是 ,平行的两直边之间的距离为 ,则该圆角正方形的周长是.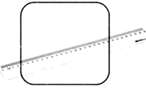 13. 如图,一把折扇展开后的圆心角为120°,扇骨 长为 ,扇面宽 ,则该折扇的扇面的面积 .
13. 如图,一把折扇展开后的圆心角为120°,扇骨 长为 ,扇面宽 ,则该折扇的扇面的面积 . 14. 如图,在半径为6的⊙O中,随意向圆内投掷一个小球,经过大量重复投掷后发现,小球落在阴影部分的概率稳定在 ,则 的长约为.(结果保留π)
14. 如图,在半径为6的⊙O中,随意向圆内投掷一个小球,经过大量重复投掷后发现,小球落在阴影部分的概率稳定在 ,则 的长约为.(结果保留π)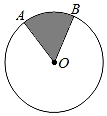 15. 如图, 是 的外接圆, , ,则弧 的长为.
15. 如图, 是 的外接圆, , ,则弧 的长为.三、解答题
-
16. 如图, 的半径 , 于点C, .求 的长.
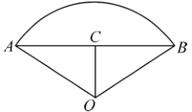 17. 如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,图中的三个扇形(即三个阴影部分)的面积之和是多少?弧长的和为多少?
17. 如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,图中的三个扇形(即三个阴影部分)的面积之和是多少?弧长的和为多少? 18. 已知圆环的大圆半径R=4cm,小圆半径r=2cm,求圆环的面积。
18. 已知圆环的大圆半径R=4cm,小圆半径r=2cm,求圆环的面积。 19. 如图,已知 是 的直径,C,D是 上的点, ,交 于点E,连结 .
19. 如图,已知 是 的直径,C,D是 上的点, ,交 于点E,连结 .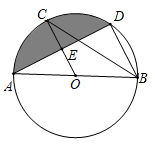 (1)、求证: ;(2)、若 , ,求图中阴影部分的面积.20. 已知△ABC在平面直角坐标系中的位置如图所示.
(1)、求证: ;(2)、若 , ,求图中阴影部分的面积.20. 已知△ABC在平面直角坐标系中的位置如图所示. (1)、画出△ABC绕点C按顺时针方向旋转90°后的△A'B'C';(2)、旋转后点A'的坐标为;B'的坐标为.(3)、求点A旋转到A'所经过的路线长(结果保留π)21. 如图,在平面直角坐标系xOy中,边长为4的正方形ABCD的中心在原点O处,且AB∥x轴,点P在正方形ABCD的边上,点P从点A处沿A→B→C→D→A→B→…匀速运动,以点P为圆心,以1为半径长画圆,在运动过程中:
(1)、画出△ABC绕点C按顺时针方向旋转90°后的△A'B'C';(2)、旋转后点A'的坐标为;B'的坐标为.(3)、求点A旋转到A'所经过的路线长(结果保留π)21. 如图,在平面直角坐标系xOy中,边长为4的正方形ABCD的中心在原点O处,且AB∥x轴,点P在正方形ABCD的边上,点P从点A处沿A→B→C→D→A→B→…匀速运动,以点P为圆心,以1为半径长画圆,在运动过程中: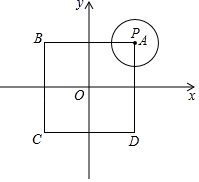 (1)、当⊙P第1次与x轴相切时,则圆心P的坐标为;(直接写出结果)(2)、当圆心P的运动路程为2019时,判断⊙P与y轴的位置关系,并说明理由;(3)、当⊙P第一次回到出发的位置时,即⊙P运动一周,求⊙P运动一周覆盖平面的区域的面积.
(1)、当⊙P第1次与x轴相切时,则圆心P的坐标为;(直接写出结果)(2)、当圆心P的运动路程为2019时,判断⊙P与y轴的位置关系,并说明理由;(3)、当⊙P第一次回到出发的位置时,即⊙P运动一周,求⊙P运动一周覆盖平面的区域的面积.