初中数学湘教版九年级下册2.5.4三角形的内切圆 同步练习
试卷更新日期：2021-03-14 类型：同步测试
一、单选题
-
1. 到三角形三边的距离都相等的点是这个三角形的（ ）A、三条中线的交点 B、三条高的交点 C、三条边的垂直平分线的交点 D、三条角平分线的交点2. 根据圆规作图的痕迹，可用直尺成功找到三角形内心的是（ ）A、
B、
C、
D、
3. 下列关于三角形的内心说法正确的是（ ）A、内心是三角形三条角平分线的交点 B、内心是三角形三边中垂线的交点 C、内心到三角形三个顶点的距离相等 D、钝角三角形的内心在三角形外4. 1.下列说法中，不正确的是（ ）A、三角形的内心是三角形三条内角平分线的交点 B、锐角三角形、直角三角形、钝角三角形的内心都在三角形内部 C、垂直于半径的直线是圆的切线 D、三角形的内心到三角形的三边的距离相等5. 如图，已知⊙O是△ABC的内切圆，且∠ABC=50°，∠ACB=80°.则∠BOC等于（ ）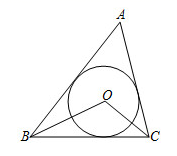
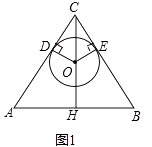
A、125° B、120° C、115° D、100°6. 如图，正三角形的内切圆半径为1，那么这个正三角形的边长为（ ）
A、2 B、3 C、 D、7. 《九章算术》中有一题“今有勾八步，股十五步，问勾中容圆径几何? ”其意思是：“今有直角三角形，勾(短直角边)长为 步，股(长直角边)长为 步，问该直角三角形能容纳的圆形(内切圆)直径是（ ）
A、6步 B、7步 C、8步 D、9步8. 如图，△ABC中，下面说法正确的个数是（ ）
①若O是△ABC的外心，∠A=50°，则∠BOC=100°；②若O是△ABC的内心，∠A=50°，则∠BOC=115°；③若BC=6，AB+AC=10，则△ABC的面积的最大值是12；④△ABC的面积是12，周长是16，则其内切圆的半径是1.
A、1个 B、2个 C、3个 D、4个9. 如图，I点为△ABC的内心，D点在BC上，且ID⊥BC，若∠B=44°，∠C=56°，则∠AID的度数为何？（ ）
A、174 B、176 C、178 D、18010. 若一直角三角形的斜边长为c，内切圆半径是r，则内切圆的面积与三角形面积之比是（ ）A、 B、 C、 D、二、填空题
-
11. 如图，在△ABC中，AC=6cm，BC=8cm，AB=10cm，则△ABC内切圆的半径为cm．
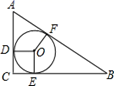12. 如图，Rt△ABC中，∠C＝90°，AC＝30cm，BC＝40cm，现利用该三角形裁剪一个最大的圆，则该圆半径是cm.
13. 设O为△ABC的内心，若∠A=48°，则∠BOC=°．14. 如图是一块直角三角形木料， ， ， ，木工师傅要从中裁下一块圆形用料，则可裁圆形木料的最大半径为.
15. 如图所示，⊙I是Rt△ABC的内切圆，点D、E、F分别是且点，若∠ACB=90°，AB=5cm，BC=4cm，则⊙I的周长为cm．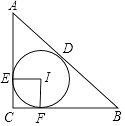
三、解答题
-
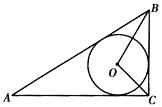
16. 已知：如图，⊙O内切于△ABC，∠BOC=105°，∠ACB=90°，AB=20cm．求BC、AC的长．
17. 已知：如图，△ABC三边BC=a，CA=b，AB=c，它的内切圆O的半径长为r．求△ABC的面积S．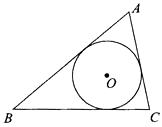
18. 已知：如图，⊙O是Rt△ABC的内切圆，∠C=90°．
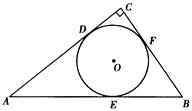(1)、若AC=12cm，BC=9cm，求⊙O的半径r；
(2)、若AC=b，BC=a，AB=c，求⊙O的半径r．
