初中数学湘教版九年级下册2.5.3切线长定理 同步练习
试卷更新日期:2021-03-14 类型:同步测试
一、单选题
-
1. 如图,P为圆O外一点, 分别切圆O于 两点,若 ,则 ( ).
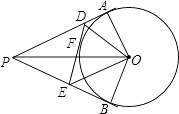
 A、2 B、3 C、4 D、52. 如图, 、 、 与圆O相切, ,则 ( )
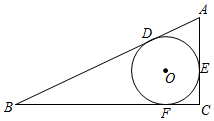
A、2 B、3 C、4 D、52. 如图, 、 、 与圆O相切, ,则 ( ) A、50° B、60° C、70° D、80°3. 如图,AD , AE分别是⊙O的切线,D , E为切点,BC切⊙O于F , 交AD , AE于点B , C , 若AD=8.则三角形ABC的周长是( )
A、50° B、60° C、70° D、80°3. 如图,AD , AE分别是⊙O的切线,D , E为切点,BC切⊙O于F , 交AD , AE于点B , C , 若AD=8.则三角形ABC的周长是( )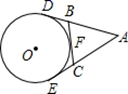 A、8 B、10 C、16 D、不能确定4. 如图,AB、AC是圆O的两条切线,切点为B、C且∠BAC=50°,D是优弧BDC上一动点(不与B、C重合),则∠BDC的度数为( )
A、8 B、10 C、16 D、不能确定4. 如图,AB、AC是圆O的两条切线,切点为B、C且∠BAC=50°,D是优弧BDC上一动点(不与B、C重合),则∠BDC的度数为( )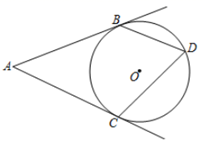 A、130° B、65° C、50°或130° D、65°或115°5. 如图, 切 于点 切 于点 交 于点 ,下列结论中不一定成立的是( )
A、130° B、65° C、50°或130° D、65°或115°5. 如图, 切 于点 切 于点 交 于点 ,下列结论中不一定成立的是( )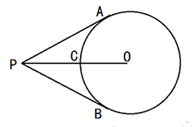 A、 B、 平分 C、 D、6. 如图PA,PB分别与 相切于A,B两点.若 ,则 的度数为( )
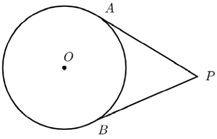
A、 B、 平分 C、 D、6. 如图PA,PB分别与 相切于A,B两点.若 ,则 的度数为( )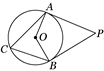 A、 B、 C、 D、7. 如图,AB,BC,CD,DA都是⊙O的切线,已知AD=2,BC=5,则AB+CD的值是( )
A、 B、 C、 D、7. 如图,AB,BC,CD,DA都是⊙O的切线,已知AD=2,BC=5,则AB+CD的值是( )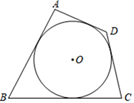 A、14 B、12 C、9 D、78. 如图,AB,AC,BD是⊙O的切线,切点分别是P,C,D.若AC=5,BD=3,则AB的长是( )
A、14 B、12 C、9 D、78. 如图,AB,AC,BD是⊙O的切线,切点分别是P,C,D.若AC=5,BD=3,则AB的长是( ) A、2 B、4 C、6 D、89. 《九章算术》是我国古代内容极为丰富的数学名著,书中有这样一个问题:“今有勾八步,股十五步,问勾中容圆,径几何?”其意思是:“如图,今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”此问题中,该内切圆的直径是( )
A、2 B、4 C、6 D、89. 《九章算术》是我国古代内容极为丰富的数学名著,书中有这样一个问题:“今有勾八步,股十五步,问勾中容圆,径几何?”其意思是:“如图,今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”此问题中,该内切圆的直径是( )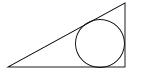 A、5步 B、6步 C、8步 D、10步10. 如图,是用一把直尺、含60°角的直角三角板和光盘摆放而成,点 为60°角与直尺交点,点 为光盘与直尺唯一交点,若 ,则光盘的直径是( ).
A、5步 B、6步 C、8步 D、10步10. 如图,是用一把直尺、含60°角的直角三角板和光盘摆放而成,点 为60°角与直尺交点,点 为光盘与直尺唯一交点,若 ,则光盘的直径是( ).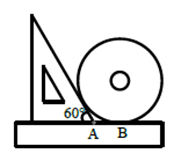 A、 B、 C、6 D、3
A、 B、 C、6 D、3二、填空题
-
11. 如图,PA、PB是⊙O的切线,若∠APO=25°,则∠BPA= .
 12. 如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过弧DE (不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为 .
12. 如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过弧DE (不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为 . 13. 如图,PA、PB、DE切分别切⊙O于点A、B、C,若∠P=50°,则∠DOE=°.
13. 如图,PA、PB、DE切分别切⊙O于点A、B、C,若∠P=50°,则∠DOE=°.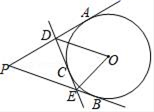 14. 如图,直线PA过半圆的圆心O,交半圆于A,B两点,PC切半圆与点C,已知PC=3,PB=1,则该半圆的半径为 .
14. 如图,直线PA过半圆的圆心O,交半圆于A,B两点,PC切半圆与点C,已知PC=3,PB=1,则该半圆的半径为 .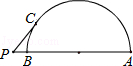 15. 如图,已知圆O内切于五边形ABCDE,切点分别是M、N、P、Q、R,且AB=5,BC=7,CD=8,DE=9,EA=4,则 的值是 .
15. 如图,已知圆O内切于五边形ABCDE,切点分别是M、N、P、Q、R,且AB=5,BC=7,CD=8,DE=9,EA=4,则 的值是 .
三、解答题