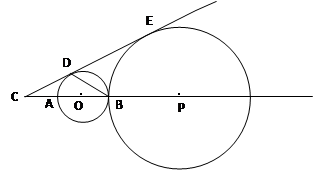初中数学湘教版九年级下册2.5.2圆的切线 同步练习
试卷更新日期:2021-03-14 类型:同步测试
一、单选题
-
1. 如图所示,AE切⊙D于点E,AC=CD=DB=10,则线段AE的长为( )
 A、10 B、15 C、10 D、202. 以O为中心点的量角器与直角三角板ABC如图摆放,直角顶点B在零刻度线所在直线DE上,且量角器与三角板只有一个公共点P,则∠CBD的度数是( )
A、10 B、15 C、10 D、202. 以O为中心点的量角器与直角三角板ABC如图摆放,直角顶点B在零刻度线所在直线DE上,且量角器与三角板只有一个公共点P,则∠CBD的度数是( )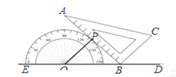 A、45°10' B、44°50' C、46°10' D、不能确定3. 已知⊙O的半径为5,直线EF经过⊙O上一点P(点E,F在点P的两旁),下列条件能判定直线EF与⊙O相切的是( )
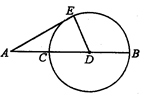
A、45°10' B、44°50' C、46°10' D、不能确定3. 已知⊙O的半径为5,直线EF经过⊙O上一点P(点E,F在点P的两旁),下列条件能判定直线EF与⊙O相切的是( ) A、OP=5 B、OE=OF C、O到直线EF的距离是4 D、OP⊥EF4. 如图,AB是半圆O的直径,点C在半圆上(不与A,B重合), 于点D,交BC于点F,下列条件中能判别CE是切线的是( )
A、OP=5 B、OE=OF C、O到直线EF的距离是4 D、OP⊥EF4. 如图,AB是半圆O的直径,点C在半圆上(不与A,B重合), 于点D,交BC于点F,下列条件中能判别CE是切线的是( )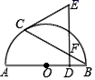 A、 B、 C、 D、5. 如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心O.若∠B=20°,则∠C的大小等于( )
A、 B、 C、 D、5. 如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心O.若∠B=20°,则∠C的大小等于( ) A、20° B、25° C、40° D、50°6. 如图所示,在直角坐标系中,A点坐标为(-3,-2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小时,P点的坐标为( )
A、20° B、25° C、40° D、50°6. 如图所示,在直角坐标系中,A点坐标为(-3,-2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小时,P点的坐标为( )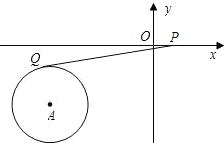 A、(-3,0) B、(-2,0) C、(-4,0)或(-2,0) D、(-4,0)7. 已知 和 外切于 , 是 和 的外公切线, , 为切点,若 , ,则 到 的距离是( )
A、(-3,0) B、(-2,0) C、(-4,0)或(-2,0) D、(-4,0)7. 已知 和 外切于 , 是 和 的外公切线, , 为切点,若 , ,则 到 的距离是( )
A、 B、 C、 D、8. 如图,P为圆O外一点,OP交圆O于A点,且OA=2AP.甲、乙两人想作一条通过P点且与圆O相切的直线,其作法如下:(甲)以P为圆心,OP长为半径画弧,交圆O于B点,则直线PB即为所求;
(乙)作OP的中垂线,交圆O于B点,则直线PB即为所求.
对于甲、乙两人的作法,下列判断何者正确?( )
 A、两人皆正确 B、两人皆错误 C、甲正确,乙错误 D、甲错误,乙正确9. 下列直线是圆的切线的是( )
A、两人皆正确 B、两人皆错误 C、甲正确,乙错误 D、甲错误,乙正确9. 下列直线是圆的切线的是( )
A、与圆有公共点的直线 B、到圆心的距离等于半径的直线 C、垂直于圆的半径的直线 D、过圆直径外端点的直线10. 如图,PA、PB是⊙O的切线,AC是⊙O直径,∠c=55°,则∠APB等于( ) A、55° B、60° C、65° D、70°
A、55° B、60° C、65° D、70°二、填空题
-
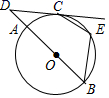
11. 如图,AB是⊙O的直径,点C在⊙O上,过点C的切线与BA的延长线交于点D,点E在弧BC上(不与点B,C重合),连接BE,CE.若∠D=40°,则∠BEC=度.
 12. 如图,直线 a⊥b ,垂足为H,点P在直线b上, ,O为直线b上一动点,若以 为半径的 与直线a相切,则 的长为.
12. 如图,直线 a⊥b ,垂足为H,点P在直线b上, ,O为直线b上一动点,若以 为半径的 与直线a相切,则 的长为.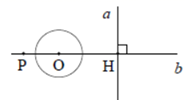 13. 如图,在 中, , ,点 在边 上,以点 为圆心作⊙ .当⊙ 恰好同时与边 , 相切时,⊙ 的半径长为.
13. 如图,在 中, , ,点 在边 上,以点 为圆心作⊙ .当⊙ 恰好同时与边 , 相切时,⊙ 的半径长为.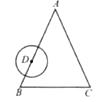 14. 如图,点A、B、D在⊙O上,∠A=25°,OD的延长线交直线BC于点C,且∠OCB=40°,直线BC与⊙O的位置关系为 .
14. 如图,点A、B、D在⊙O上,∠A=25°,OD的延长线交直线BC于点C,且∠OCB=40°,直线BC与⊙O的位置关系为 . 15. 如图,△ABC的一边AB是⊙O的直径,请你添加一个条件,使BC是⊙O的切线,你所添加的条件为 .
15. 如图,△ABC的一边AB是⊙O的直径,请你添加一个条件,使BC是⊙O的切线,你所添加的条件为 .
三、解答题
-
16. 如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O分别交CA,CB于点E,F,点G是AD的中点.求证:GE是⊙O的切线.
 17. 已知在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,以AD为弦作⊙O,使圆心O在AB上.
17. 已知在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,以AD为弦作⊙O,使圆心O在AB上.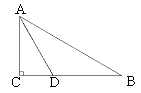 (1)、用直尺和圆规在图中作出⊙O(不写作法,保留作图痕迹) ;(2)、求证:BC为⊙O的切线.18. AB为⊙O的直径,C是⊙O上的一点,D在AB的延长线上,且∠DCB=∠A,
(1)、用直尺和圆规在图中作出⊙O(不写作法,保留作图痕迹) ;(2)、求证:BC为⊙O的切线.18. AB为⊙O的直径,C是⊙O上的一点,D在AB的延长线上,且∠DCB=∠A, (1)、CD与⊙O相切吗?如果相切,请你加以证明;如果不相切,请说明理由。(2)、若∠D=30°,BD=10cm,求⊙O的半径。
(1)、CD与⊙O相切吗?如果相切,请你加以证明;如果不相切,请说明理由。(2)、若∠D=30°,BD=10cm,求⊙O的半径。