人教版数学八年级下册 第十八章 平行四边形 18.2.1 矩形 同步练习
试卷更新日期:2021-03-14 类型:同步测试
一、单选题
-
1. 如图,在矩形OABC中,点B的坐标是(2,5),则A,C两点间的距离是( )
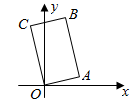 A、 B、3 C、 D、52. 如图,在矩形 中,两条对角线 与 相交于点 , , ,则 的长为( )
A、 B、3 C、 D、52. 如图,在矩形 中,两条对角线 与 相交于点 , , ,则 的长为( )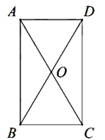 A、5 B、 C、 D、3. 如图 ,阴影部分是一个长方形,则长方形的面积是( )
A、5 B、 C、 D、3. 如图 ,阴影部分是一个长方形,则长方形的面积是( )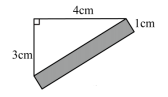 A、 B、 C、 D、4. 如图,矩形 中,对角线 , 交于O点.若 , ,则 的长为( )
A、 B、 C、 D、4. 如图,矩形 中,对角线 , 交于O点.若 , ,则 的长为( )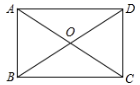 A、4 B、 C、3 D、55. 在▱ABCD中,AC与BD相交于点O,要使四边形ABCD是矩形,还需添加一个条件,这个条件可以是( )A、AO=CO B、AO=BO C、AO⊥BO D、∠OBC=∠OBA6. 如图所示,四边形ABCD的对角线为AC,BD,且 ,则下列条件能判定四边形ABCD是矩形的是( )
A、4 B、 C、3 D、55. 在▱ABCD中,AC与BD相交于点O,要使四边形ABCD是矩形,还需添加一个条件,这个条件可以是( )A、AO=CO B、AO=BO C、AO⊥BO D、∠OBC=∠OBA6. 如图所示,四边形ABCD的对角线为AC,BD,且 ,则下列条件能判定四边形ABCD是矩形的是( )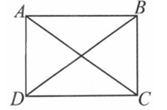 A、 B、AC,BD互相平分 C、 D、7. ABCD添加下列条件后,仍不能使它成为矩形的是( )A、AB⊥BC B、AC=BD C、∠A=∠B D、BC= CD8. 如图,点P是Rt△ABC中斜边AC (不与A,C重合)上一动点,分别作PM⊥AB于点M,作PN⊥BC于点N,连接BP、MN,若AB=6,BC=8,当点P在斜边AC上运动时,则MN的最小值是( )
A、 B、AC,BD互相平分 C、 D、7. ABCD添加下列条件后,仍不能使它成为矩形的是( )A、AB⊥BC B、AC=BD C、∠A=∠B D、BC= CD8. 如图,点P是Rt△ABC中斜边AC (不与A,C重合)上一动点,分别作PM⊥AB于点M,作PN⊥BC于点N,连接BP、MN,若AB=6,BC=8,当点P在斜边AC上运动时,则MN的最小值是( )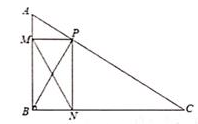 A、1.5 B、2 C、4.8 D、2.49. 如图,已知点P为长方形 内一点(不含边界),设 ,若 ,则( )
A、1.5 B、2 C、4.8 D、2.49. 如图,已知点P为长方形 内一点(不含边界),设 ,若 ,则( )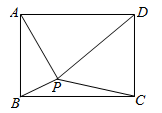 A、 B、 C、 D、10. 如图,点P是 中斜边AC(不与A,C重合)上一动点,分别作PM⊥AB于点M,作PN⊥BC于点N,点O是MN的中点,若AB=6;BC=8,当点P在AC上运动时,则BO的最小值是( )
A、 B、 C、 D、10. 如图,点P是 中斜边AC(不与A,C重合)上一动点,分别作PM⊥AB于点M,作PN⊥BC于点N,点O是MN的中点,若AB=6;BC=8,当点P在AC上运动时,则BO的最小值是( ) A、1.5 B、2 C、2.4 D、2.5
A、1.5 B、2 C、2.4 D、2.5二、填空题
-
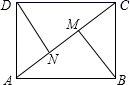
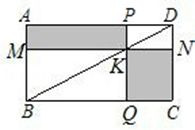
11. 杨师傅要做一个长方形的桌面,做好后量得长为2m,宽为1.5m,对角线为2.15m,则这个桌面.(填“合格”或“不合格”).12. 如下图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ , 那么图中矩形AMKP的面积 与矩形QCNK的面积 的大小关系是 (填“>”或“<”或“=”).
 13. 如图,矩形 中, , ,点P是 边上动点,则 的最小值为.
13. 如图,矩形 中, , ,点P是 边上动点,则 的最小值为.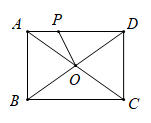 14. 如图,矩形 的对角线 与 交于点 ,过点 作 的垂线分别交 于 两点.若 ,则 的长度为 , 等于 .
14. 如图,矩形 的对角线 与 交于点 ,过点 作 的垂线分别交 于 两点.若 ,则 的长度为 , 等于 .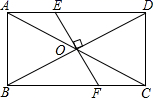
三、解答题
-
15. 如图,已知E是矩形ABCD一边AD的中点,延长AB至点F连接CE,EF,CF,得到 .且 , , .求CE的长;
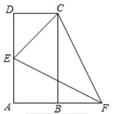 16. 如图,△ABC中,AC=BC,CD⊥AB于点D,四边形DBCE是平行四边形.求证:四边形ADCE是矩形.
16. 如图,△ABC中,AC=BC,CD⊥AB于点D,四边形DBCE是平行四边形.求证:四边形ADCE是矩形.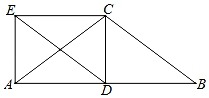 17. 如图,在等边△ABC中,点D是AC的中点,点F是BC的中点,以BD为边作等边△BDE , 连结点A、E . 求证:四边形AEBF为矩形.
17. 如图,在等边△ABC中,点D是AC的中点,点F是BC的中点,以BD为边作等边△BDE , 连结点A、E . 求证:四边形AEBF为矩形.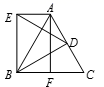
四、综合题