初中数学湘教版九年级下册2.3垂径定理 同步练习
试卷更新日期：2021-03-14 类型：同步测试
一、单选题
-
1. 如图，⊙O的直径长10，弦AB=8，M是弦AB上的动点，则OM的长的取值范围是（ ）
A、3≤OM≤5 B、4≤OM≤5 C、3＜OM＜5 D、4＜OM＜52. 如图，AB为⊙O的直径，弦CD⊥AB于E，已知CD=12，BE=2，则⊙O的半径为（ ）
A、8 B、10 C、16 D、203. 下列说法正确的是（ ）A、弦是直径 B、平分弦的直径垂直于弦 C、优弧一定大于劣弧 D、等弧所对的圆心角相等4. 如图，AB是⊙O的弦，OC⊥AB交⊙O于点 C，点D是⊙O上一点，∠ADC=25°，则∠BOC的度数为（ ）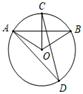
A、30° B、40° C、50° D、60°5. 如图，AB是⊙O的直径，弦CD⊥AB，垂足为M，下列结论不成立的是（ ）
A、CM=DM B、 C、∠ACD=∠ADC D、OM=MD6.如图，在⊙O中，弦AB与直径CD垂直，垂足为E，则下列结论中错误的是（ ）
A、AE=BE B、CE=DE C、AC=BC D、AD=BD7. 如图，AB是⊙O的直径，C是⊙O上一点，若AC︰BC＝ ︰ ，AB＝10cm，OD⊥BC于点D，则BD的长为（ ）.
A、 cm B、3cm C、5cm D、6cm8. 在⊙O中，弦AB的长为2 cm，圆心O到AB的距离为1cm，则⊙O的半径是（ ）A、2 B、3 C、 D、9. 《九章算术》是我国古代第一部自成体系的数学专著，代表了东方数学的最高成就．它的算法体系至今仍在推动着计算机的发展和应用．书中记载：“今有圆材埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”译为：“今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯这木材，锯口深1寸（ED=1寸），锯道长1尺（AB=1尺=10寸）”，问这块圆柱形木材的直径是多少？”如图所示，请根据所学知识计算：圆柱形木材的直径AC是（ ）
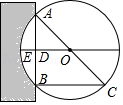A、13寸 B、20寸 C、26寸 D、28寸10. 已知⊙O的半径是10cm， 是120°，那么弦AB的弦心距是（ ）
A、5cm B、 cm C、 cm D、 cm二、填空题
-
11. 如图，AB是圆O的直径，CD⊥AB于点E，交圆O于点D，OF⊥AC于点F，BD=5，则OF=.
12. 如图， 中， ， ，则 .
13. 如图，已知AB是⊙O的直径，弦CD交AB于点E，∠CEA＝30°，OF⊥CD，垂足为点F，DE＝5，OF＝1，那么CD＝ ．
14. 为了改善市区人民的生活环境，某市建设污水管网工程，某圆柱型水管的直径为100cm，截面如图所示，若管内的污水的面宽AB=60cm，则污水的最大深度为 ．
三、解答题
-
15. 如图为桥洞的形状，其正视图是由 和矩形ABCD构成．O点为 所在⊙O的圆心，点O又恰好在AB为水面处．若桥洞跨度CD为8米，拱高（OE⊥弦CD于点F ）EF为2米．求 所在⊙O的半径DO．
