初中数学湘教版九年级下册2.2.2圆周角 同步练习
试卷更新日期:2021-03-14 类型:同步测试
一、单选题
-
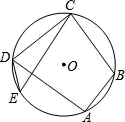
1. 如图,四边形ABCD是 的内接四边形,若 ,则 等于( )
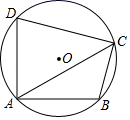
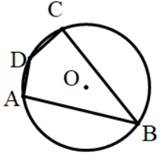 A、 B、 C、 D、2. 如图,四边形 是 的内接四边形, ,则 的度数为( )
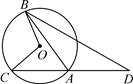
A、 B、 C、 D、2. 如图,四边形 是 的内接四边形, ,则 的度数为( ) A、70° B、90° C、100° D、110°3. 如图,AB是⊙O的直径,点C,D在⊙O上, = ,OD∥AC,下列结论错误的是( )
A、70° B、90° C、100° D、110°3. 如图,AB是⊙O的直径,点C,D在⊙O上, = ,OD∥AC,下列结论错误的是( )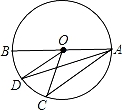 A、∠C=∠D B、∠BOD=∠COD C、∠BAD=∠CAD D、∠BOD=∠BAC4. 下列图形中,∠B=2∠A的是( )A、
A、∠C=∠D B、∠BOD=∠COD C、∠BAD=∠CAD D、∠BOD=∠BAC4. 下列图形中,∠B=2∠A的是( )A、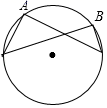 B、
B、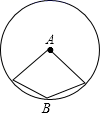 C、
C、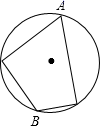 D、
D、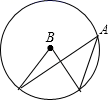 5. 如图,将 沿弦AB折叠,圆弧恰好经过圆心O,点P是优弧 上一点,则 的度数为
5. 如图,将 沿弦AB折叠,圆弧恰好经过圆心O,点P是优弧 上一点,则 的度数为 A、 B、 C、 D、6. 如图,AB为 的直径,点C,点D是 上的两点,连接CA,CD,AD.若 ,则 的度数是( )
A、 B、 C、 D、6. 如图,AB为 的直径,点C,点D是 上的两点,连接CA,CD,AD.若 ,则 的度数是( ) A、110° B、120° C、130° D、140°7. 如图,转盘中点A,B,C在圆上,∠4=40°,∠B=60° ,让转盘绕圆心O自由转动,当转盘停止时指针指向区域III的概率是( )
A、110° B、120° C、130° D、140°7. 如图,转盘中点A,B,C在圆上,∠4=40°,∠B=60° ,让转盘绕圆心O自由转动,当转盘停止时指针指向区域III的概率是( )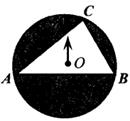 A、 B、 C、 D、8. 如图,在⊙O中,点B是弧AC上的一点,∠AOC=140°,则∠ABC的度数为( )
A、 B、 C、 D、8. 如图,在⊙O中,点B是弧AC上的一点,∠AOC=140°,则∠ABC的度数为( )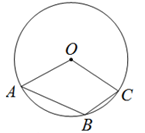 A、70° B、110° C、120° D、140°9. 如图,△ABC内接于⊙O,∠A=45°,⊙O的半径为2,则BC的长为( )
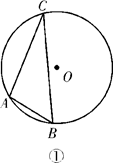
A、70° B、110° C、120° D、140°9. 如图,△ABC内接于⊙O,∠A=45°,⊙O的半径为2,则BC的长为( ) A、2 B、 C、2 D、410. 圆内接四边形ABCD,∠A,∠B,∠C的度数之比为3∶4∶6,则∠D的度数为( )A、60° B、80° C、100° D、120°
A、2 B、 C、2 D、410. 圆内接四边形ABCD,∠A,∠B,∠C的度数之比为3∶4∶6,则∠D的度数为( )A、60° B、80° C、100° D、120°二、填空题
-
11. 如图所示,点A,B,C是⊙O上三点,∠AOB=110°,则∠ACB=°.
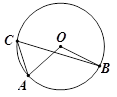 12. ⊙O的半径为1,弦AB= ,点C是圆上异于A、B的一动点,则∠ACB=.13. 如图,⊙O与正六边形OABCDE的边OA、OE分别交于点F、G;则 所对的圆周角∠FPG的大小为度。
12. ⊙O的半径为1,弦AB= ,点C是圆上异于A、B的一动点,则∠ACB=.13. 如图,⊙O与正六边形OABCDE的边OA、OE分别交于点F、G;则 所对的圆周角∠FPG的大小为度。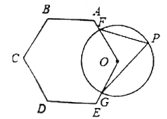 14. 在⊙O中,圆心角∠AOB=80°,点P是圆上不同于点A、B的点,则∠APB=°.15. 阅读以下作图过程:
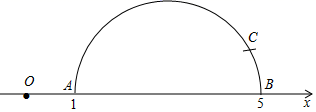
14. 在⊙O中,圆心角∠AOB=80°,点P是圆上不同于点A、B的点,则∠APB=°.15. 阅读以下作图过程:第一步:在数轴上,点O表示数0,点A表示数1,点B表示数5,以AB为直径作半圆(如图);
第二步:以B点为圆心,1为半径作弧交半圆于点C(如图);
第三步:以A点为圆心,AC为半径作弧交数轴的正半轴于点M.
请你在下面的数轴中完成第三步的画图(保留作图痕迹,不写画法),并写出点M表示的数为 .
三、解答题
-
16. 如图,AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=30°,求∠BOC的度数.