2016年海南省中考数学试卷

试卷更新日期：2016-07-21 类型：中考真卷

进入出卷网下载

一、选择题

1. 2016的相反数是（）

A、2016 B、﹣2016 C、 $\frac{1}{2016}$ D、﹣ $\frac{1}{2016}$

查看试题解析
2. 若代数式x+2的值为1，则x等于（）

A、1 B、﹣1 C、3 D、﹣3

查看试题解析
3.
如图是由四个相同的小正方体组成的几何体，则它的主视图为（）

A、 B、 C、 D、

查看试题解析
4. 某班7名女生的体重（单位：kg）分别是35、37、38、40、42、42、74，这组数据的众数是（）

A、74 B、44 C、42 D、40

查看试题解析
5. 下列计算中，正确的是（）

A、（a³）⁴=a¹² B、a³•a⁵=a¹⁵ C、a²+a²=a⁴ D、a⁶÷a²=a³

查看试题解析
6. 省政府提出2016年要实现180 000农村贫困人口脱贫，数据180 000用科学记数法表示为（）

A、1.8×10³ B、1.8×10⁴ C、1.8×10⁵ D、1.8×10⁶

查看试题解析
7. 解分式方程 $\frac{1}{x - 1} + 1 = 0$ ，正确的结果是（）

A、x=0 B、x=1 C、x=2 D、无解

查看试题解析
8. 面积为2的正方形的边长在（）

A、0和1之间 B、1和2之间 C、2和3之间 D、3和4之间

查看试题解析
9.
某村耕地总面积为50公顷，且该村人均耕地面积y（单位：公顷/人）与总人口x（单位：人）的函数图象如图所示，则下列说法正确的是（）

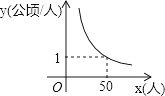A、该村人均耕地面积随总人口的增多而增多 B、该村人均耕地面积y与总人口x成正比例 C、若该村人均耕地面积为2公顷，则总人口有100人 D、当该村总人口为50人时，人均耕地面积为1公顷

查看试题解析
10. 在平面直角坐标系中，将△AOB绕原点O顺时针旋转180°后得到△A₁OB₁ ，若点B的坐标为（2，1），则点B的对应点B₁的坐标为（）

A、（1，2） B、（2，﹣1） C、（﹣2，1） D、（﹣2，﹣1）

查看试题解析
11. 三张外观相同的卡片分别标有数字1、2、3，从中随机一次抽出两张，这两张卡片上的数字恰好都小于3的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{1}{6}$ D、 $\frac{1}{9}$

查看试题解析
12.
如图，AB是⊙O的直径，直线PA与⊙O相切于点A，PO交⊙O于点C，连接BC．若∠P=40°，则∠ABC的度数为（）

A、20° B、25° C、40° D、50°

查看试题解析
13.
如图，矩形ABCD的顶点A、C分别在直线a、b上，且a∥b，∠1=60°，则∠2的度数为（）

A、30° B、45° C、60° D、75°

查看试题解析
14.
如图，AD是△ABC的中线，∠ADC=45°，把△ADC沿着直线AD对折，点C落在点E的位置．如果BC=6，那么线段BE的长度为（）

A、6 B、6 $\sqrt{2}$ C、2 $\sqrt{3}$ D、3 $\sqrt{2}$

查看试题解析

二、填空题

15. 因式分解：ax﹣ay=

查看试题解析
16. 某工厂去年的产值是a万元，今年比去年增加10%，今年的产值是万元．

查看试题解析
17.
如图，AB是⊙O的直径，AC、BC是⊙O的弦，直径DE⊥AC于点P．若点D在优弧上，AB=8，BC=3，则DP=

查看试题解析
18.
如图，四边形ABCD是轴对称图形，且直线AC是对称轴，AB∥CD，则下列结论：①AC⊥BD；②AD∥BC；③四边形ABCD是菱形；④△ABD≌△CDB．其中正确的是（只填写序号）

查看试题解析

三、解答题

19. 计算：

(1)、6÷（﹣3）+ $\sqrt{4}$ ﹣8×2^﹣²；

(2)、解不等式组： ${\begin{cases} x - 1 < 2 \\ \frac{x + 1}{2} \geq 1 \end{cases}$ ．

查看试题解析
20. 世界读书日，某书店举办“书香”图书展，已知《汉语成语大词典》和《中华上下五千年》两本书的标价总和为150元，《汉语成语大词典》按标价的50%出售，《中华上下五千年》按标价的60%出售，小明花80元买了这两本书，求这两本书的标价各多少元．

查看试题解析
21.
在太空种子种植体验实践活动中，为了解“宇番2号”番茄，某校科技小组随机调查60株番茄的挂果数量x（单位：个），并绘制如下不完整的统计图表：
“宇番2号”番茄挂果数量统计表
挂果数量x（个）
频数（株）
频率
25≤x＜35
6
0.1
35≤x＜45
12
0.2
45≤x＜55
a
0.25
55≤x＜65
18
b
65≤x＜75
9
0.15
请结合图表中的信息解答下列问题：

(1)、统计表中，a= ， b=；

(2)、将频数分布直方图补充完整；

(3)、若绘制“番茄挂果数量扇形统计图”，则挂果数量在“35≤x＜45”所对应扇形的圆心角度数为°；

(4)、若所种植的“宇番2号”番茄有1000株，则可以估计挂果数量在“55≤x＜65”范围的番茄有株．

查看试题解析
22.
如图，在大楼AB的正前方有一斜坡CD，CD=4米，坡角∠DCE=30°，小红在斜坡下的点C处测得楼顶B的仰角为60°，在斜坡上的点D处测得楼顶B的仰角为45°，其中点A、C、E在同一直线上．

(1)、求斜坡CD的高度DE；

(2)、求大楼AB的高度（结果保留根号）

查看试题解析
23.
如图1，在矩形ABCD中，BC＞AB，∠BAD的平分线AF与BD、BC分别交于点E、F，点O是BD的中点，直线OK∥AF，交AD于点K，交BC于点G．

(1)、求证：①△DOK≌△BOG；②AB+AK=BG；

(2)、若KD=KG，BC=4﹣ $\sqrt{2}$ ．
①求KD的长度；
②如图2，点P是线段KD上的动点（不与点D、K重合），PM∥DG交KG于点M，PN∥KG交DG于点N，设PD=m，当S_△_PMN= $\frac{\sqrt{2}}{4}$ 时，求m的值．

查看试题解析
24.
如图1，抛物线y=ax²﹣6x+c与x轴交于点A（﹣5，0）、B（﹣1，0），与y轴交于点C（0，﹣5），点P是抛物线上的动点，连接PA、PC，PC与x轴交于点D．

(1)、求该抛物线所对应的函数解析式；

(2)、若点P的坐标为（﹣2，3），请求出此时△APC的面积；

(3)、过点P作y轴的平行线交x轴于点H，交直线AC于点E，如图2．
①若∠APE=∠CPE，求证： $\frac{A E}{E C} = \frac{3}{7}$ ；
②△APE能否为等腰三角形？若能，请求出此时点P的坐标；若不能，请说明理由．

查看试题解析

挂果数量x（个）	频数（株）	频率
25≤x＜35	6	0.1
35≤x＜45	12	0.2
45≤x＜55	a	0.25
55≤x＜65	18	b
65≤x＜75	9	0.15