2016年广西南宁市中考数学试卷
试卷更新日期:2016-07-21 类型:中考真卷
一、选择题
-
1. ﹣2的相反数是( )A、﹣2 B、-4 C、2 D、42.
把一个正六棱柱如图1摆放,光线由上向下照射此正六棱柱时的正投影是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 据《南国早报》报道:2016年广西高考报名人数约为332000人,创历史新高,其中数据332000用科学记数法表示为( )A、0.332×106 B、3.32×105 C、3.32×104 D、33.2×1044. 已知正比例函数y=3x的图象经过点(1,m),则m的值为( )A、 B、3 C、﹣ D、﹣35. 某校规定学生的学期数学成绩满分为100分,其中研究性学习成绩占40%,期末卷面成绩占60%,小明的两项成绩(百分制)依次是80分,90分,则小明这学期的数学成绩是( )A、80分 B、82分 C、84分 D、86分6.
3. 据《南国早报》报道:2016年广西高考报名人数约为332000人,创历史新高,其中数据332000用科学记数法表示为( )A、0.332×106 B、3.32×105 C、3.32×104 D、33.2×1044. 已知正比例函数y=3x的图象经过点(1,m),则m的值为( )A、 B、3 C、﹣ D、﹣35. 某校规定学生的学期数学成绩满分为100分,其中研究性学习成绩占40%,期末卷面成绩占60%,小明的两项成绩(百分制)依次是80分,90分,则小明这学期的数学成绩是( )A、80分 B、82分 C、84分 D、86分6.如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是( )
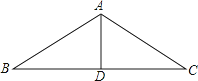 A、5sin36°米 B、5cos36°米 C、5tan36°米 D、10tan36°米7. 下列运算正确的是( )A、a2﹣a=a B、ax+ay=axy C、m2•m4=m6 D、(y3)2=y58. 下列各曲线中表示y是x的函数的是( )A、
A、5sin36°米 B、5cos36°米 C、5tan36°米 D、10tan36°米7. 下列运算正确的是( )A、a2﹣a=a B、ax+ay=axy C、m2•m4=m6 D、(y3)2=y58. 下列各曲线中表示y是x的函数的是( )A、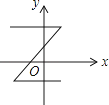 B、
B、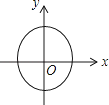 C、
C、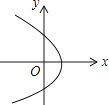 D、
D、 9.
9.如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为( )
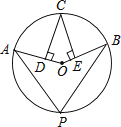 A、140° B、70° C、60° D、40°10. 超市店庆促销,某种书包原价每个x元,第一次降价打“八折”,第二次降价每个又减10元,经两次降价后售价为90元,则得到方程( )A、0.8x﹣10=90 B、0.08x﹣10=90 C、90﹣0.8x=10 D、x﹣0.8x﹣10=9011.
A、140° B、70° C、60° D、40°10. 超市店庆促销,某种书包原价每个x元,第一次降价打“八折”,第二次降价每个又减10元,经两次降价后售价为90元,则得到方程( )A、0.8x﹣10=90 B、0.08x﹣10=90 C、90﹣0.8x=10 D、x﹣0.8x﹣10=9011.有3个正方形如图所示放置,阴影部分的面积依次记为S1 , S2 , 则S1:S2等于( )
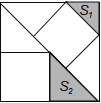 A、1: B、1:2 C、2:3 D、4:912.
A、1: B、1:2 C、2:3 D、4:912.二次函数y=ax2+bx+c(a≠0)和正比例函数y= x的图象如图所示,则方程ax2+(b﹣ )x+c=0(a≠0)的两根之和( )
 A、大于0 B、等于0 C、小于0 D、不能确定
A、大于0 B、等于0 C、小于0 D、不能确定二、填空题
-
13. 若二次根式 有意义,则x的取值范围是
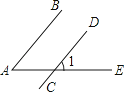
14.如图,平行线AB,CD被直线AE所截,∠1=50°,则∠A=
 15. 分解因式:a2﹣9=
15. 分解因式:a2﹣9=
16.如图,在4×4正方形网格中,有3个小正方形已经涂黑,若再涂黑任意一个白色的小正方形(每一个白色的小正方形被涂黑的可能性相同),使新构成的黑色部分的图形是轴对称图形的概率是
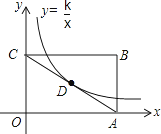
 17.
17.如图所示,反比例函数y= (k≠0,x>0)的图象经过矩形OABC的对角线AC的中点D.若矩形OABC的面积为8,则k的值为
 18.
18.观察下列等式:
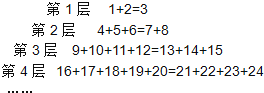
在上述数字宝塔中,从上往下数,2016在第层.
三、解答题
-
19. 计算:|﹣2|+4cos30°﹣( )﹣3+ .20. 解不等式组 ,并把解集在数轴上表示出来.21.
如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4)
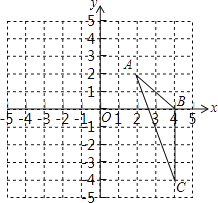 (1)、请画出△ABC向左平移6个单位长度后得到的△A1B1C1;(2)、以点O为位似中心,将△ABC缩小为原来的 ,得到△A2B2C2 , 请在y轴右侧画出△A2B2C2 , 并求出∠A2C2B2的正弦值.22.
(1)、请画出△ABC向左平移6个单位长度后得到的△A1B1C1;(2)、以点O为位似中心,将△ABC缩小为原来的 ,得到△A2B2C2 , 请在y轴右侧画出△A2B2C2 , 并求出∠A2C2B2的正弦值.22.在图“书香八桂,阅读圆梦”读数活动中,某中学设置了书法、国学、诵读、演讲、征文四个比赛项目(每人只参加一个项目),九(2)班全班同学都参加了比赛,该班班长为了了解本班同学参加各项比赛的情况,收集整理数据后,绘制以下不完整的折线统计图(图1)和扇形统计图(图2),根据图表中的信息解答下列各题:
 (1)、请求出九(2)全班人数;(2)、请把折线统计图补充完整;(3)、南南和宁宁参加了比赛,请用“列表法”或“画树状图法”求出他们参加的比赛项目相同的概率.23.
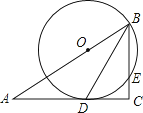
(1)、请求出九(2)全班人数;(2)、请把折线统计图补充完整;(3)、南南和宁宁参加了比赛,请用“列表法”或“画树状图法”求出他们参加的比赛项目相同的概率.23.如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
 (1)、求证:AC是⊙O的切线;(2)、若OB=10,CD=8,求BE的长.24. 在南宁市地铁1号线某段工程建设中,甲队单独完成这项工程需要150天,甲队单独施工30天后增加乙队,两队又共同工作了15天,共完成总工程的 .
(1)、求证:AC是⊙O的切线;(2)、若OB=10,CD=8,求BE的长.24. 在南宁市地铁1号线某段工程建设中,甲队单独完成这项工程需要150天,甲队单独施工30天后增加乙队,两队又共同工作了15天,共完成总工程的 .
(1)、求乙队单独完成这项工程需要多少天?(2)、为了加快工程进度,甲、乙两队各自提高工作效率,提高后乙队的工作效率是 ,甲队的工作效率是乙队的m倍(1≤m≤2),若两队合作40天完成剩余的工程,请写出a关于m的函数关系式,并求出乙队的最大工作效率是原来的几倍?25.已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.
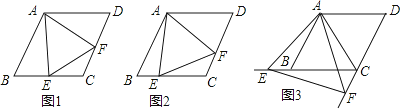 (1)、如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;(2)、如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;(3)、如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.26.
(1)、如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;(2)、如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;(3)、如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.26.如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x﹣2交于B,C两点.
 (1)、求抛物线的解析式及点C的坐标;(2)、求证:△ABC是直角三角形;(3)、若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式及点C的坐标;(2)、求证:△ABC是直角三角形;(3)、若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.