江苏省泰州市2020-2021学年高一上学期数学期末考试试卷

试卷更新日期：2021-03-12 类型：期末考试

进入出卷网下载

一、单选题

1. 设集合 $M = {x | x > - 1}$ ，集合 $N = {x | - 2 < x < 1}$ ，则 $M \cap N =$ （）

A、 $(- 2, - 1)$ B、 $(- 1, 1)$ C、 $(- 1, + \infty)$ D、 $(- 2, + \infty)$

查看试题解析
2. 函数 $f (x) = {\begin{array}{l} 2^{x}, x > 0, \\ x + 3, x \leq 0, \end{array}$ 则 $f (f (- 2))$ 的值为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、2 D、4

查看试题解析
3. 已知 $a = \log_{2.1} 0.3, b = {0.3}^{2.1}, c = {2.1}^{0.3}$ ，则a，b，c的大小关系是（）

A、b>c>a B、c>a>b C、b>a>c D、c>b>a

查看试题解析
4. 2020年11月24日凌晨4时30分，我国在文昌航天发射场用长征五号遥五运载火箭把嫦娥五号探测器顺利地送入预定轨道，开启我国首次外太空采样返回之旅｡据科学家们测算：火箭的最大速度至少达11.2千米/秒时，可将嫦娥五号探测器顺利送入外太空｡若火箭的最大速度v(单位：米/秒)､燃料的质量M(单位：吨)和嫦娥五号探测器的质量m(单位：吨)近似满足函数关系式 $v = 5600 \cdot \lg (1 + \frac{M}{m}) ，$ V=当燃料质量与嫦娥五号探测器质量的比值至少为（）顺利送入外太空.

A、9 B、99 C、999 D、9999

查看试题解析
5. 方程 $e^{x} + x - 2 = 0$ （其中 $e = 2.71828 \dots$ ）的近似解所在的区间是（）

A、 $(0, \frac{1}{2})$ B、 $(\frac{1}{2}, 1)$ C、 $(1, \frac{3}{2})$ D、 $(\frac{3}{2}, 2)$

查看试题解析
6. 英国数学家泰勒(B. Taylor，1685-1731)以发现泰勒公式和泰勒级数闻名于世｡由泰勒公式，我们能得到 $e = 1 + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \dots + \frac{1}{n!} + \frac{e^{θ}}{(n + 1)!}$ (其中e为自然对数的底数， $0 < θ < 1, n! = n \times (n - 1) \times (n - 2) \times ... \times 2 \times 1$ )，其拉格朗日余项是 $R_{n} = \frac{e^{θ}}{(n + 1)!} .$ 可以看出，右边的项用得越多，计算得到的e的近似值也就越精确｡若 $\frac{3}{(n + 1)!}$ 近似地表示e的泰勒公式的拉格朗日余项 $R_{n},$ $R_{n}$ 不超过 $\frac{1}{1000}$ 时，正整数n的最小值是（）

A、5 B、6 C、7 D、8

查看试题解析
7. 现有四个函数：①y=x|sinx|，②y=x²cosx，③y=x·e^x；④ $y = x + \frac{1}{x}$ 的图象(部分)如下，但顺序被打乱，则按照从左到右将图象对应的函数序号安排正确的一组是（）

A、①②③④ B、①③②④ C、②①③④ D、③②①④

查看试题解析
8. 设函数 $f (x) = {\begin{array}{l} 4 x - 2 ， x \leq 1 ， \\ \log_{2} (x + 3) ， x > 1 ， \end{array}$ 则满足不等式 $f (x) + f (x - \frac{1}{4}) > 2$ 的x的取值范围是（）

A、 $(\frac{- 23 + \sqrt{257}}{8} ， + \infty]$ B、 $(\frac{7}{8} ， 1]$ C、 $(1 ， \frac{5}{4}]$ D、 $(\frac{7}{8} ， + \infty)$

查看试题解析

二、多选题

9. 设函数 $f (x) = {(\frac{1}{2})}^{| x |}$ ，下列说法正确的是（）

A、函数 $f (x)$ 是偶函数 B、函数 $f (x)$ 是奇函数 C、函数 $f (x)$ 有最大值 $1$ D、函数 $f (x)$ 在 $(- \infty ， 0)$ 上单调递减

查看试题解析
10. 下列说法正确的是（）

A、若定义在 $R$ 上的函数 $f (x)$ 满足 $f (- 1) = f (1)$ ，则 $f (x)$ 是偶函数 B、若定义在 $R$ 上的函数 $f (x)$ 满足 $f (- 1) \neq f (1)$ ，则 $f (x)$ 不是偶函数 C、若定义在 $R$ 上的函数 $f (x)$ 满足 $f (- 1) < f (1)$ ，则 $f (x)$ 在 $R$ 上是增函数 D、若定义在 $R$ 上的函数 $f (x)$ 满足 $f (- 1) < f (1)$ ，则 $f (x)$ 在 $R$ 上不是减函数

查看试题解析
11. 函数f(x)=Asin(ωx+φ)(其中 $A > 0 ， ω > 0 ， | φ | \leq \frac{π}{2})$ 的部分图象如图所示，则（）

A、函数f(x)的最小正周期是2π B、函数f(x)的图象关于点 $(\frac{2 π}{3} ， 0)$ 对称 C、函数f(x)的图象关于直线 $x = \frac{π}{3}$ 对称 D、将函数f(x)的图象向右平移 $\frac{π}{6}$ 个单位后，所得的函数图象关于y轴对称

查看试题解析
12. 双曲函数是一类与常见的三角函数类似的函数.最基本的双曲函数是双曲正弦函数 $s h x = \frac{e^{x} - e^{- x}}{2}$ 和双曲余弦函数 $c h x = \frac{e^{x} + e^{- x}}{2}$ ，其中 $e$ 是自然对数的底数.则下列结论正确的是（）

A、 $c h 2 x = c h^{2} x + s h^{2} x$ B、 $s h 2 x = c h^{2} x - s h^{2} x$ C、 $s h (x + y) = s h x c h y + c h x s h y$ D、 $c h (x + y) = c h x c h y + s h x s h y$

查看试题解析

三、填空题

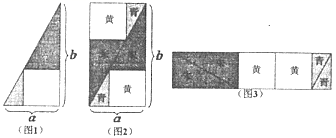
13. 命题“ $\exists$ x∈R，x²+x+1≤0”的否定是．

查看试题解析
14. 已知幂函数 $f (x) = x^{α}$ 的图象过点 $(3 ， \sqrt{3})$ ，则 $f (x) =$ .

查看试题解析
15. 已知函数f(x)的定义域为R，对任意的实数x，有f(1-x)=f(1+x)，当x≤1时， $f (x) = e^{x} + x$ ，则不等式 $f (2 x - 1) \geq f (x + 1)$ 的解集为.

查看试题解析
16. “勾股容方”问题出自我国汉代数学名著《九章算术》，该问题可以被描述为：“设一直角三角形(如图1)的两直角边长分别为a和b，求与该直角三角形具有公共直角的内接正方形的边长”，公元263年，数学家刘徽为《九章算术》作注，在注中他利用出入相补原理给出了上述问题如图2和图3所示的解答，则图1中与直角三角形具有公共直角的内接正方形的边长为，当内接正方形的面积为1时，则图3中两个标有“朱”的三角形和两个标有“青”的三角形的面积总和的最小值为.

查看试题解析

四、解答题

17. 计算：

(1)、 ${(\frac{9}{4})}^{\frac{1}{2}} - {(- 8)}^{0} + \sqrt[5]{{(- 1)}^{5}} + {(0.5)}^{- 1}$ ；

(2)、 ${(\lg 2)}^{2} + \lg 5 \times \lg 2 + \lg 5 + \ln$ 1.

查看试题解析
18. 已知集合 $A = {x | x^{2} - 5 x - 6 \leq 0},$ B={x|(x-m)(x-m-6)≤0}，其中m∈R.

(1)、当m=2时，求A∪B；

(2)、若“x∈A”是“ $x \in ∁_{R} B$ ”的充分条件，求m的取值范围.

查看试题解析
19. 已知θ为锐角，在以下三个条件中任选一个：
① $\frac{\cos (2 π - θ) \sin (3 π + θ)}{\sin (\frac{π}{2} + θ) \tan (π - θ)} = \frac{1}{2}$ ；② $2 \sin^{2} θ - \cos θ - 1 = 0$ ；③ $\frac{\cos (θ - π)}{\sin (π + θ)} \cdot \sin (θ - \frac{π}{2}) \cdot \cos (\frac{π}{2} + θ) = \frac{1}{4}$ ；并解答以下问题：

(1)、若选 ▲ (填序号)，求θ的值；

(2)、在（1）的条件下，求函数y= tan(2x+θ)的定义域､周期和单调区间｡

查看试题解析
20. 已知函数 $f (x) = \ln \frac{a^{x} + b^{x}}{2}$ ，其中a>0且a≠1，b>0且b≠1；

(1)、若f(x)为偶函数，试确定a， b满足的等量关系；

(2)、已知 $n \in N^{*}$ ，试比较f(n)和 $\frac{f (2 n)}{2}$ 的大小关系，并证明你的结论.

查看试题解析

21. 某同学用“五点法”画函数

f (x) = A sin (ω x + φ) + B

(其中A>0，0>0，

| φ | < \frac{π}{2})

在某一个周期内的图象时，列表并填入部分数据，如表：

ωx+φ	0	$\frac{π}{2}$	π	$\frac{3π}{2}$	2π
x			$\frac{π}{3}$		$\frac{5π}{6}$
Asin(ωx+φ)+B		3		-1

(1)、请根据上表中的部分数据，求出函数f(x)的解析式；

(2)、若定义在区间

[- \frac{π}{4}, \frac{π}{4}]

上的函数g(x)=af(x)+b的最大值为7，最小值为1，求实数a，b的值.

查看试题解析

22. 已知函数 $f (x) = x^{2} - 2 m x + m^{2} + 6$ ， $g (x) = 2^{x}$ .

(1)、求 $g (f (m))$ 的值；

(2)、若方程 $g (f (x)) = 128$ 在区间 $[- 1, 2]$ 上有唯一的解，求实数 $m$ 的取值范围；

(3)、对任意 $m \in R$ ，若关于 $x$ 的不等式 $f (g (x)) + f (g (- x)) \geq t [g (x) + g (- x)]$ 在 $x \in R$ 上恒成立，求实数 $t$ 的取值范围.

查看试题解析