甘肃省定西市安定区2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-03-12 类型：期末考试

进入出卷网下载

一、单选题

1. 下面四个手机应用图标中是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列运算正确的是（）

A、 ${(a^{2})}^{3} = a^{5}$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、 ${(a b)}^{3} = a^{3} b^{3}$ D、 $a^{6} \div a^{3} = a^{2}$

查看试题解析
3. 若分式 $\frac{x^{2} - 4}{x + 2}$ 的值为0，则x的值为（）

A、-2 B、0 C、2 D、±2

查看试题解析
4. 等腰三角形两边长为3和6，则周长为（）

A、12 B、15 C、12或15 D、无法确定

查看试题解析
5. 如果把 $\frac{x y}{x + y}$ 中 $x 、 y$ 的值都扩大 $10$ 倍，那么这个代数式的值（）

A、不变 B、扩大 $10$ 倍 C、扩大 $20$ 倍 D、扩大 $100$ 倍

查看试题解析
6. 下列等式从左到右的变形，属于因式分解的是（）

A、 $a (x - y) = a x - a y$ B、 $x^{3} - x = x (x + 1) (x - 1)$ C、 $(x + 1) (x + 3) = x^{2} + 4 x + 3$ D、 $x^{2} + 2 x + 1 = x (x + 2) + 1$

查看试题解析
7. 计算 $(\frac{a}{b} - \frac{b}{a}) \div \frac{a - b}{a}$ 的结果为（）

A、 $\frac{a + b}{b}$ B、 $\frac{a - b}{b}$ C、 $\frac{a - b}{a}$ D、 $\frac{a + b}{a}$

查看试题解析
8. 已知 $x + y = 1$ ，则 $\frac{1}{2} x^{2} + x y + \frac{1}{2} y^{2}$ ＝（）

A、 $1$ B、 $\frac{1}{2}$ C、 $2$ D、 $1$ 或 $2$

查看试题解析
9. 如图，在 $Δ A B C$ 中， $∠ C = 90^{\circ} ， ∠ A = 30^{\circ} ， A B$ 的垂直平分线交 $A C$ 于 $D$ ，交 $A B$ 于 $E ， C D = 2$ ，则 $A C$ 的长为（）

A、 $3$ B、 $4$ C、 $5$ D、 $6$

查看试题解析
10. 如图，ΔABC中，∠C=90°，AC=BC，AD平分∠CAB，交BC于D，DE⊥AB于E，且AB=6cm，则ΔDEB的周长为（）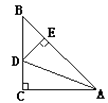

A、4cm B、6cm C、10cm D、以上都不对

查看试题解析

二、填空题

11. 计算： ${(\frac{1}{3})}^{- 1} + {(- 2)}^{0} =$ .

查看试题解析
12. 当x时，分式 $\frac{1}{x - 3}$ 有意义

查看试题解析
13. 计算： $(- 5 a^{4}) \cdot (- 8 a b^{2})$ =.

查看试题解析
14. 2020年突如其来的新型冠状病毒严重影响着人们正常的生活秩序，经专家测定，新型冠状病毒的直径大约为 $80$ 纳米 $~ 120$ 纳米， $80$ 纳米 $= 0.00000008$ 米，数据 $0.00000008$ 米用科学记数法表示为米.

查看试题解析
15. 点P关于x轴对称的点是（3，-4），则点P的坐标是.

查看试题解析
16. 已知a，b，c是△ABC的三边长，a，b满足|a﹣7|+（b﹣1）²=0，c为奇数，则c= ．

查看试题解析
17. 一个多边形的内角和是外角和的2倍，则这个多边形的边数为．

查看试题解析
18. 如图，已知点 $D$ 、点 $E$ 分别是边长为 $2 a$ 的等边三角形 $A B C$ 的边 $B C 、 A B$ 的中点，连接 $A D ，$ 点 $F$ 为 $A D$ 上的一个动点，连接 $E F 、 B F ，$ 若 $A D = b ，$ 则 $△ B E F$ 的周长的最小值是.

查看试题解析

三、解答题

19. 因式分解：

(1)、 $a^{3} b - a b$

(2)、 $- x^{2} + 4 x y - 4 y^{2}$

查看试题解析
20. 计算： $(x + 5) (x - 1) + {(x - 2)}^{2}$

查看试题解析
21. 解方程： $\frac{2}{x - 3} = \frac{3}{x}$

查看试题解析
22. 先化简，再求值： $\frac{x^{2} - 2 x + 1}{x^{2} - 1} \div (1 - \frac{3}{x + 1})$ ，其中x=0.

查看试题解析
23. 如图：求作一点 $P$ ，使 $P M = P N ，$ 并且使点 $P$ 到 $∠ A O B$ 的两边的距离相等.（不写作法，保留作图痕迹）

查看试题解析
24. 如图，在平面直角坐标系中，△ABC的顶点A（0，1），B（3，2），C（1，4）均在正方形网格的格点上．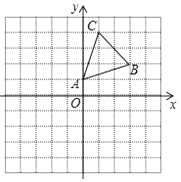

(1)、画出△ABC关于x轴的对称图形△A₁B₁C₁；

(2)、将△A₁B₁C₁沿x轴方向向左平移3个单位后得到△A₂B₂C₂ ，写出顶点A₂ ， B₂ ， C₂的坐标．

查看试题解析
25. 如图，点E，F在线段BC上，BE=CF，∠A=∠D，∠B=∠C，AF与DE交于O，求证：OE=OF.

查看试题解析
26. 已知 $a 、 b 、 c$ 是三边 $Δ A B C$ 的长，且满足 $a^{2} + b^{2} + c^{2} + 50 = 6 a + 8 b + 10 c$ ，求 $Δ A B C$ 三边的长.

查看试题解析
27. 城镇老旧小区改造是重大民生工程和发展工程；安定区积极响应党的号召，全面推进城区老旧小区改造工作.现计划对城区某小区的居民自来水管道进行改造；该工程若由甲队单独施工恰好在规定时间内完成；若乙队单独施工，则完成工程所需天数是规定天数的 $1.5$ 倍.如果由甲、乙队先合做 $15$ 天，那么余下的工程由甲队单独完成还需 $5$ 天.

(1)、这项工程的规定时间是多少天？

(2)、已知甲队每天的施工费用为 $3500$ 元，乙队每天的施工费用为 $2500$ 元.为了缩短工期以减少对居民用水的影响，工程指挥部最终决定该工程由甲、乙两队合做来完成.则该工程施工费用是多少？

查看试题解析
28. 等边△ABC中，F为边BC边上的点，作∠CBE＝∠CAF，延长AF与BE交于点D，截取BE＝AD，连接CE.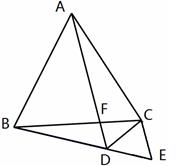

(1)、求证：CE＝CD

(2)、求证：DC平分∠ADE

(3)、试判断△CDE的形状，并说明理由.

查看试题解析