重庆市万州区2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-03-12 类型:期末考试
一、单选题
-
1. 下列各数中,为负数的是( )A、0 B、-2 C、1 D、2. 下列各组角中,∠1与∠2是对顶角的是( )A、
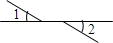 B、
B、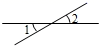 C、
C、 D、
D、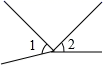 3. 代数式 的正确解释是( )A、a与b的倒数的差的平方 B、a与b的差的平方的倒数 C、a的平方与b的差的倒数 D、a的平方与b的倒数的差4. 下列几何体中,主视图为三角形的是( )A、
3. 代数式 的正确解释是( )A、a与b的倒数的差的平方 B、a与b的差的平方的倒数 C、a的平方与b的差的倒数 D、a的平方与b的倒数的差4. 下列几何体中,主视图为三角形的是( )A、 B、
B、 C、
C、 D、
D、 5. cm大约相当于( )A、数学书的厚度 B、三层楼的高度 C、姚明的高度 D、珠穆朗玛峰的高度6. 如图,点E在CD延长线上,下列条件中不能判定AC∥BD的是( )
5. cm大约相当于( )A、数学书的厚度 B、三层楼的高度 C、姚明的高度 D、珠穆朗玛峰的高度6. 如图,点E在CD延长线上,下列条件中不能判定AC∥BD的是( )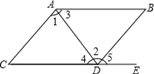 A、∠1=∠2 B、∠3=∠4 C、∠5=∠C D、∠C+∠BDC=1807. 单项式 与单项式 是同类项,则 的值是( )A、5 B、6 C、9 D、88. 已知 、 、 ,则 的值为( )A、7 B、9 C、-63 D、129. 观察下列图形,是用棋子摆成的图案,摆第1个图案要4枚棋子,摆第2个图案要7枚棋子,摆第3个图案要11枚棋子,按照这样的方式摆下去,则摆第10个图案要棋子( )枚.
A、∠1=∠2 B、∠3=∠4 C、∠5=∠C D、∠C+∠BDC=1807. 单项式 与单项式 是同类项,则 的值是( )A、5 B、6 C、9 D、88. 已知 、 、 ,则 的值为( )A、7 B、9 C、-63 D、129. 观察下列图形,是用棋子摆成的图案,摆第1个图案要4枚棋子,摆第2个图案要7枚棋子,摆第3个图案要11枚棋子,按照这样的方式摆下去,则摆第10个图案要棋子( )枚. A、57 B、60 C、67 D、7910. 若代数式 的值与x的取值无关,则 的值为( )A、0 B、﹣1 C、﹣2 D、211. 下列说法中:①两个有理数相加,和一定大于每一个加数;②在同一平面内,过一点有且只有一条直线与已知直线垂直;③多项式 是三次三项式;④两点确定一条直线.其中正确的有( )A、4个 B、3个 C、2个 D、1个12. 若 ,则x的取值范围是( )A、 B、 C、 D、
A、57 B、60 C、67 D、7910. 若代数式 的值与x的取值无关,则 的值为( )A、0 B、﹣1 C、﹣2 D、211. 下列说法中:①两个有理数相加,和一定大于每一个加数;②在同一平面内,过一点有且只有一条直线与已知直线垂直;③多项式 是三次三项式;④两点确定一条直线.其中正确的有( )A、4个 B、3个 C、2个 D、1个12. 若 ,则x的取值范围是( )A、 B、 C、 D、二、填空题
-
13. “畅游三峡,万州出发”,2020年万州共接待海内外游客2200万人次,把2200用科学记数法表示为.14. 在式子 ,0, , , 中,整式有个.15. 如图,AB表示北偏东45°方向,AC表示南偏东30°方向,则∠BAC=.
 16. 如图,AC⊥BC,AC=3,BC=4,AB=5,则点C到AB的距离为.
16. 如图,AC⊥BC,AC=3,BC=4,AB=5,则点C到AB的距离为. 17. 定义“*”是一种运算符号,规定 ,则 的值为.18. 有甲、乙两种糖果,原价分别为每千克a元和b元.根据调查,将两种糖果按甲种糖果m千克与乙种糖果n千克的比例混合,取得较好的销售效果.现在糖果价格有了调整:甲种糖果单价上涨c%,乙种糖果单价下跌d%,但按原比例混合的糖果单价恰好没变,那么 =.
17. 定义“*”是一种运算符号,规定 ,则 的值为.18. 有甲、乙两种糖果,原价分别为每千克a元和b元.根据调查,将两种糖果按甲种糖果m千克与乙种糖果n千克的比例混合,取得较好的销售效果.现在糖果价格有了调整:甲种糖果单价上涨c%,乙种糖果单价下跌d%,但按原比例混合的糖果单价恰好没变,那么 =.三、解答题
-
19. 计算:(1)、(﹣20)﹣13+4﹣(﹣27)+26(2)、20. 补全解答过程:
如图,EF∥AD,∠1=∠2,若∠BAC=70°,求∠AGD.

解:∵EF∥AD,(已知)
∴∠2= , (两直线平行,同位角相等).
又∵∠1=∠2,(已知)
∴∠1=∠3,(等量代换)
∴AB∥ , ()
∴∠AGD+∠BAC=180°.()
∵∠BAC=70°,(已知)
∴∠AGD= .
21. 如图,线段AC=6cm,线段BC=15cm,点M是AC的中点,在CB上取一点N,使得CN:NB=1:2,求MN的长. 22. 先化简,再求值: ,其中 .23. 小林同学元旦节期间参加社会实践活动,从电脑城以批发价每个40元的价格购进100个充电宝,然后每个加价m元到市场出售.由于元旦节三天假期快结束了,小林同学在成功售出60个充电宝后,决定将剩余充电宝按售价的九折出售,并很快全部售完.(1)、小林元旦节充电宝的总销售额是多少?(2)、若m=10,小林同学实际销售完这批充电宝的利润率为多少?(利润率=利润÷进价×100%)24. 如图,已知∠AOC是直角,∠BOC=46°,OE平分∠BOC,OD平分∠AOB.
22. 先化简,再求值: ,其中 .23. 小林同学元旦节期间参加社会实践活动,从电脑城以批发价每个40元的价格购进100个充电宝,然后每个加价m元到市场出售.由于元旦节三天假期快结束了,小林同学在成功售出60个充电宝后,决定将剩余充电宝按售价的九折出售,并很快全部售完.(1)、小林元旦节充电宝的总销售额是多少?(2)、若m=10,小林同学实际销售完这批充电宝的利润率为多少?(利润率=利润÷进价×100%)24. 如图,已知∠AOC是直角,∠BOC=46°,OE平分∠BOC,OD平分∠AOB.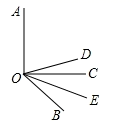 (1)、试求∠DOE的度数;(2)、当∠BOC=α(0°≤α≤90°),请问∠DOE的大小是否变化?并说明理由.25. 若一个三位数t= (其中a、b、c不全相等且都不为0),重新排列各数位上的数字必可得到一个最大数和一个最小数,此最大数和最小数的差叫做原数的差数,记为T(t).例如,539的差数T(539)=953﹣359=594.(1)、根据以上方法求出T(268)= , T(513)=;(2)、已知三位数 (其中a>b>1)的差数T( )=495,且各数位上的数字之和为3的倍数,求所有符合条件的三位数的值.26. 已知AB∥CD,CF平分∠ECD.(1)、如图1,若∠DCF=25°,∠E=20°,求∠ABE的度数.
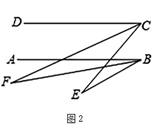
(1)、试求∠DOE的度数;(2)、当∠BOC=α(0°≤α≤90°),请问∠DOE的大小是否变化?并说明理由.25. 若一个三位数t= (其中a、b、c不全相等且都不为0),重新排列各数位上的数字必可得到一个最大数和一个最小数,此最大数和最小数的差叫做原数的差数,记为T(t).例如,539的差数T(539)=953﹣359=594.(1)、根据以上方法求出T(268)= , T(513)=;(2)、已知三位数 (其中a>b>1)的差数T( )=495,且各数位上的数字之和为3的倍数,求所有符合条件的三位数的值.26. 已知AB∥CD,CF平分∠ECD.(1)、如图1,若∠DCF=25°,∠E=20°,求∠ABE的度数.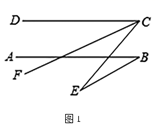 (2)、如图2,若∠EBF=2∠ABF,∠CFB的2倍与∠CEB的补角的和为190°,求∠ABE的度数.
(2)、如图2,若∠EBF=2∠ABF,∠CFB的2倍与∠CEB的补角的和为190°,求∠ABE的度数.