陕西省宝鸡市高新区2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-03-12 类型:期末考试
一、单选题
-
1. 下列调查中,适合抽样调查的是( )A、调查本班同学的平均身高 B、了解本学校老师的年龄结构 C、调查一沓钞票中有没有假钞 D、了解一批圆珠笔芯的使用寿命2. 如图所示的几何体从上面看到的图形是( )
 A、
A、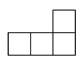 B、
B、 C、
C、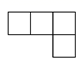 D、
D、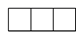 3. 中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数,如图,根据刘徽的这种表示方法,观察图①,可推算图②所得到的数值为( )
3. 中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数,如图,根据刘徽的这种表示方法,观察图①,可推算图②所得到的数值为( )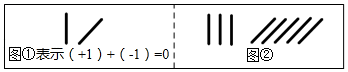 A、2 B、﹣2 C、8 D、﹣84. 下列结论正确的是( )A、﹣3ab2和b2a是同类项 B、 不是单项式 C、a比﹣a大 D、2是方程2x+1=4的解5. 下列各项变形错误的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则6. 一个角的补角,等于这个角的余角的 倍,则这个角是( )A、30° B、35° C、40° D、45°7. 如果 ,那么代数式 的值是( )A、 B、3 C、 D、58. 下列说法中,其中正确的个数有( )
A、2 B、﹣2 C、8 D、﹣84. 下列结论正确的是( )A、﹣3ab2和b2a是同类项 B、 不是单项式 C、a比﹣a大 D、2是方程2x+1=4的解5. 下列各项变形错误的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则6. 一个角的补角,等于这个角的余角的 倍,则这个角是( )A、30° B、35° C、40° D、45°7. 如果 ,那么代数式 的值是( )A、 B、3 C、 D、58. 下列说法中,其中正确的个数有( )①两点之间的所有连线中,线段最短;
②倒数等于它本身的数是 、 、 ;
③不能作射线 的延长线;
④单项式 的系数是 ,次数是 ;
⑤若 ,则 ;
⑥方程 是关于 的一元一次方程,则 .
A、 个 B、 个 C、 个 D、 个9. 相传有个人不讲究说话艺术常引起误会,一天他摆宴席请客,他看到还有几个人没来,就自言自语:“怎么该来的还不来啊?”客人听了心里想难道我们是不该来的,于是有一半客人走了.他一看十分着急,又说:“不该走的倒走了!”剩下的人一听,是我们该走啊!又有剩下的三分之二的人离开了.他着急地一拍大腿,连说:“我说的不是他们.”于是最后剩下的四个人也都告辞走了.聪明的你能知道刚开始来的客人个数是( )A、24 B、18 C、16 D、1510. 减去它的 ,再减去余下的 ,再减去余下的 ,....,以此类推,一直减到余下的 ,则最后剩下的数是( )A、 B、 C、 D、二、填空题
-
11. 根据世卫组织最新实时统计数据,截至北京时间 月 日 时 分,全球累计新冠肺炎确诊病例约 万例,用科学记数法表示 万例为例.12. 如图,折叠围成一个正方体时,数字 会在与数字 所在的平面相对的平面上.
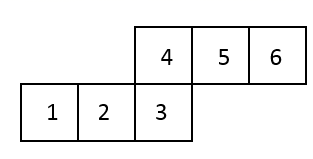 13. 已知多项式 与多项式 的和是 ,则多项式 是.14. 某服装进货价为 元/件,商店提高进价的 进行标价,为回馈新、老顾客商店元旦期间进行大促销活动,将此服装打折销售,但销售后商店仍可获利 ,则该服装应打折销售.15. 如图,下列图案由边长均等的黑、白两色正方形按一定规律拼接而成,按此规律,第n个图案中白色正方形的个数为个.
13. 已知多项式 与多项式 的和是 ,则多项式 是.14. 某服装进货价为 元/件,商店提高进价的 进行标价,为回馈新、老顾客商店元旦期间进行大促销活动,将此服装打折销售,但销售后商店仍可获利 ,则该服装应打折销售.15. 如图,下列图案由边长均等的黑、白两色正方形按一定规律拼接而成,按此规律,第n个图案中白色正方形的个数为个.
三、解答题
-
16. 计算:(1)、 ;(2)、 .17. 解方程:(1)、 ;(2)、 .18. 周口某中学积极开展“晨阳体育”活动,共开设了跳绳、体操、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如图不完整的条形统计图和扇形统计图(部分信息未给出).
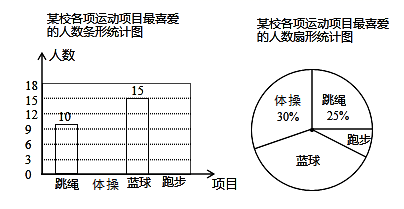 (1)、求本次调查学生的人数;(2)、求喜爱体操、跑步的人数,并补全条形统计图;(3)、求喜爱篮球、跑步的人数占调查人数的百分比.19. 定义一种新运算;观察下列各式;(1)、请你想一想: ;(2)、若 ,那么 (填“ ”或“ ” );(3)、先化简,再求值: ,其中 , .20. 如图所示,有理数 , , 在数轴上的对应点分别是 、 、 ,原点为点 .
(1)、求本次调查学生的人数;(2)、求喜爱体操、跑步的人数,并补全条形统计图;(3)、求喜爱篮球、跑步的人数占调查人数的百分比.19. 定义一种新运算;观察下列各式;(1)、请你想一想: ;(2)、若 ,那么 (填“ ”或“ ” );(3)、先化简,再求值: ,其中 , .20. 如图所示,有理数 , , 在数轴上的对应点分别是 、 、 ,原点为点 . (1)、化简: ;(2)、若 为线段 的中点, , ,求 值.21. 如图,直线 与 相交于点 , , , , 平分 .
(1)、化简: ;(2)、若 为线段 的中点, , ,求 值.21. 如图,直线 与 相交于点 , , , , 平分 . (1)、求 的度数;(2)、求 的度数.22. 某市按以下规定收取每月水费;每立方米水费包括基本水费和污水处理费两部分.基本水费实行阶段收费;若每月每户不超过20m3 , 则每立方米基本水费按 元收费;若超过20m3则超过部分每立方米按 元收费;污水处理费每立方米均按 元收取.(1)、若当月用水量为x(m3),请你用含 的式子表示当月所付水费金额;(2)、如果某户居民在某月所交水费的平均价为每立方米 元,那么这个月这户居民共用多少立方米的水?23. 如图, 是线段 上一点, , 、 两点分别从 、 出发以 、 的速度同时向左运动( 在线段 上, 在线段 上),运动时间为 .
(1)、求 的度数;(2)、求 的度数.22. 某市按以下规定收取每月水费;每立方米水费包括基本水费和污水处理费两部分.基本水费实行阶段收费;若每月每户不超过20m3 , 则每立方米基本水费按 元收费;若超过20m3则超过部分每立方米按 元收费;污水处理费每立方米均按 元收取.(1)、若当月用水量为x(m3),请你用含 的式子表示当月所付水费金额;(2)、如果某户居民在某月所交水费的平均价为每立方米 元,那么这个月这户居民共用多少立方米的水?23. 如图, 是线段 上一点, , 、 两点分别从 、 出发以 、 的速度同时向左运动( 在线段 上, 在线段 上),运动时间为 . (1)、若 、 运动 时,且 ,求 的长;(2)、若 、 运动到任一时刻时,总有 , 的长度是否变化?若不变,请求出 的长;若变化,请说明理由;(3)、在(2)的条件下, 是直线 上一点,且 ,求 的长.
(1)、若 、 运动 时,且 ,求 的长;(2)、若 、 运动到任一时刻时,总有 , 的长度是否变化?若不变,请求出 的长;若变化,请说明理由;(3)、在(2)的条件下, 是直线 上一点,且 ,求 的长.