江苏省连云港市2020-2021学年七年级上学期数学期末考试试卷

试卷更新日期：2021-03-12 类型：期末考试

进入出卷网下载

一、单选题

1. -2的相反数是（）

A、1 B、2 C、-1 D、-2

查看试题解析
2. 单项式 $- a^{2} b$ 的系数和次数分别是（）

A、0，-2 B、1，3 C、-1，2 D、-1，3

查看试题解析
3. 有一个几何体模型，甲同学：它的侧面是曲面；乙同学：它只有一个底面，且是圆形.则该模型对应的立体图形可能是（）

A、三棱柱 B、三棱锥 C、圆锥 D、圆柱

查看试题解析
4. 下列计算正确的是（）

A、 $3 a - a = 2$ B、 $x + x = x^{2}$ C、 $3 m n - 3 n m = 0$ D、 $3 a - (a - b) = 2 a - b$

查看试题解析
5. 如图，数轴上A，B两点分别对应实数a，b，则下列结论正确的是（）

A、 $a + b > 0$ B、 $a - b > 0$ C、 $a b > 0$ D、 $| a | - | b | > 0$

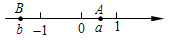查看试题解析
6. 2020年12月30日，连云港市图书馆新馆正式开馆.小明同学从家步行去图书馆，他以5km/h的速度行进24min后，爸爸骑自行车以15km/h的速度按原路追赶小明.爸爸从出发到途中与小明会合用了多少时间?设爸爸出发 $x h$ 后与小明会合，那么所列方程正确的是（）

A、 $5 x = 15 (x + \frac{24}{60})$ B、 $5 (x + 24) = 15 x$ C、 $5 x = 15 (x + 24)$ D、 $5 (x + \frac{24}{60}) = 15 x$

查看试题解析
7. 如图，在方格纸中，三角形 $A B C$ 经过变换得到三角形 $D E F$ ，正确的变换是（）

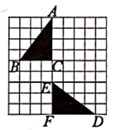A、把三角形 $A B C$ 向下平移4格，再绕点 $C$ 逆时针方向旋转180° B、把三角形 $A B C$ 向下平移5格，再绕点 $C$ 顺时针方向旋转180° C、把三角形 $A B C$ 绕点 $C$ 逆时针方向旋转90°，再向下平移2格 D、把三角形 $A B C$ 绕点 $C$ 顺时针方向旋转90°，再向下平移5格

查看试题解析
8. 如图，图1是一个三阶金字塔魔方，它是由若干个小三棱锥堆成的一个大三棱锥（图2），把大三棱锥的四个面都涂上颜色.若把其中1个面涂色的小三棱锥叫中心块，2个面涂色的叫棱块，3个面涂色的叫角块，则三阶金字塔魔方中“（棱块数）+（角块数）-（中心块数）”得（）

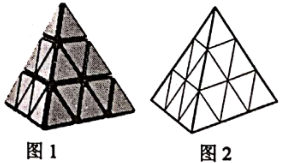A、2 B、-2 C、0 D、4

查看试题解析

二、填空题

9. 比较大小：-2020-2021（填“>”，“<”或“=”）.

查看试题解析
10. 连淮扬镇铁路于2020年12月全线开通，北起连云港，经淮安、扬州，跨长江后终至江苏南部镇江，线路全长约304公里，设计时速为250公里，总投资金额约4580000万元，其中数据“4580000”用科学记数法表示为.

查看试题解析
11. 将面积为2的正方形按如图方式放在数轴上，以原点为圆心，正方形的边长为半径，用圆规画出数轴上的一个点 $A$ ，点 $A$ 表示的数是.（填“有理数”或“无理数”）

查看试题解析
12. 如果 $2 a + b = 1$ ，那么 $4 a + 2 b - 1$ 的值等于.

查看试题解析

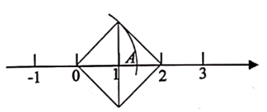13. 牛顿在他的《普遍的算术》一书中写道：“要解答一个含有数量间的抽象关系的问题，只要把题目由日常语言译成代数语言就行了.”请阅读下表，并填写表中空白.

日常语言	代数语言
连云港到南京的城际列车在连云港站出发时车上有一些乘客	$x$
到灌云站时无人下车，有10人上车	$x + 10$
到灌南站时有1人下车后，又有车上人数的 $\frac{1}{9}$ 人上车

查看试题解析

14. 五巧板是七巧板的变形，也是由一个正方形分割而成的，图中与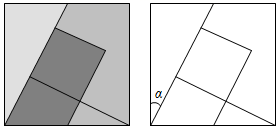 $∠ α$ 互余的角有个.

查看试题解析
15. 按如图的程序计算.若输入的 $x = - 1$ ，输出的 $y = 0$ ，则 $a =$ .

查看试题解析
16. 如图1， $О$ 为直线 $A B$ 上一点，作射线 $O C$ ，使 $∠ A O C = 120 °$ ，将一个直角三角尺如图摆放，直角顶点在点 $О$ 处，一条直角边 $O P$ 在射线 $O A$ 上.将图1中的三角尺绕点 $О$ 以每秒10°的速度按逆时针方向旋转（如图2所示），在旋转一周的过程中，第 $t$ 秒时， $O P$ 所在直线恰好平分 $∠ A O C$ ，则 $t$ 的值为.

查看试题解析

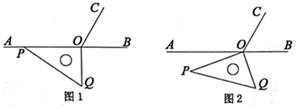
三、解答题

17. 计算：

(1)、 $2 \times {(- 3)}^{3} - 4 \times (- 3)$ ；

(2)、 $- 2^{2} \div (\frac{1}{2} \div \frac{1}{3}) \times (- \frac{5}{8})$ .

查看试题解析
18. 化简：

(1)、 $x^{2} - 5 x y + y x + 2 x^{2}$ ；

(2)、 $2 (3 a b - 2 c) + 3 (- 2 a b + 5 a)$ .

查看试题解析
19. 解下列方程：

(1)、 $2 x - 1 = 5 x - 7$ ；

(2)、 $\frac{x + 1}{2} - 1 = \frac{2 - 3 x}{3}$ .

查看试题解析
20. 如图是一个高脚碗，高度约为6.2cm，闲置时可以将碗摞起来摆放，4个碗摞起来的高度为13.4cm.

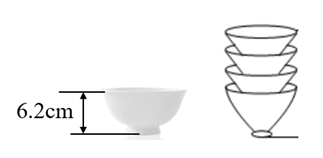(1)、每多摞一个碗，高度增加cm；

(2)、若摞起来的高度为20.6cm，求共有几个碗摞在一起?（用方程解决）

查看试题解析
21. 在如图所示的方格中，每个小正方形的边长为1，点 $A 、 B 、 C 、 D$ 在方格纸中小正方形的顶点上.

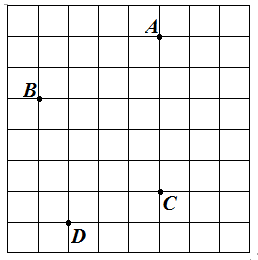(1)、画线段 $A B$ ；

(2)、画图并说理：
①画出点 $C$ 到线段 $A B$ 的最短线路 $C E$ ，写出理由；

②画出一点 $P$ ，使 $A P + D P + C P + E P$ 最短，写出理由.

查看试题解析
22. 如图，直线AB、CD相交于点O，射线OE、OF分别平分 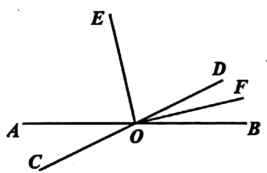$∠ A O D$ 、 $∠ B O D$ ， $∠ A O C = 26 °$ .

(1)、求 $∠ B O F$ 的度数；

(2)、判断射线OE、OF之间有怎样的位置关系？并说明理由.

查看试题解析
23. 下图是某几何体的表面展开图：

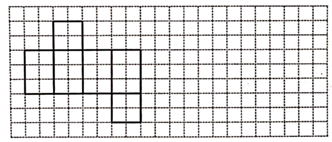(1)、这个几何体的名称是；

(2)、若该几何体的主视图是正方形，请在网格中画出该几何体的左视图、俯视图；

(3)、若网格中每个小正方形的边长为1，则这个几何体的体积为.

查看试题解析
24. 某超市先后以每千克12元和每千克14元的价格两次共购进大葱800千克，且第二次付款是第一次付款的1.5倍.

(1)、求两次各购进大葱多少千克?

(2)、该超市以每千克18元的标价销售这批大葱，售出500千克后，受市场影响，把剩下的大葱标价每千克22元，并打折全部售出.已知销售这批大葱共获得利润4440元，求超市对剩下的大葱是打几折销售的?（总利润=销售总额-总成本）

查看试题解析
25. 将网格中相邻的两个数分别加上同一个数，称为一步变换.比如，我们可以用三步变换将网格1变成网格2，变换过程如图：

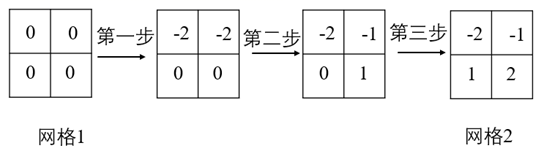(1)、用两步变换将网格3变成网格4，请在网格中填写第一步变换后的结果；

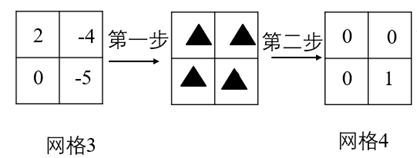(2)、若网格5经过三步变换可以变成网格6，求x的值（不用填写网格）；

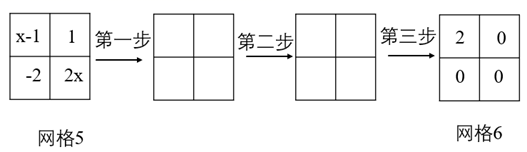(3)、若网格7经过若干步变换可以变成网格8，请直接写出a、b之间满足的关系.

查看试题解析
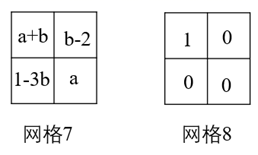26. 如图1，将一段长为60cm绳子AB拉直铺平后折叠（绳子无弹性，折叠处长度忽略不计），使绳子与自身一部分重叠.

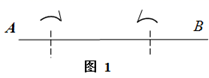(1)、若将绳子AB沿M、N点折叠，点A、B分别落在 $A^{'}$ 、 $B^{'}$ 处.
①如图2，若 $A^{'}$ 、 $B^{'}$ 恰好重合于点О处，MN= cm；

②如图3，若点 $A^{'}$ 落在点 $B^{'}$ 的左侧，且 $A^{'} B^{'} = 20 cm$ ，MN= cm；

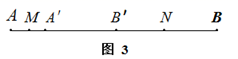
③若 $A^{'} B^{'} = n cm$ ，MN= cm.（用含n的代数式表示）

(2)、如图4，若将绳子AB沿N点折叠后，点B落在 $B^{'}$ 处，在重合部分 $B^{'} N$ 上沿绳子垂直方向剪断，将绳子分为三段，若这三段的长度由短到长的比为3：4：5，直接写出AN所有可能的长度.

查看试题解析