河南省新乡市卫辉市2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-03-12 类型:期末考试
一、单选题
-
1. 在1,-2,0,53这四个数中,最大的数是( )A、-2 B、0 C、53 D、12. 过度包装既浪费资源又污染环境,据测算,如果全国每年减少十分之一的包装纸用量,那么能减少3120000吨二氧化碳的排放量,把数据3120000用科学记数法表示为( )A、312×104 B、3.12×106 C、0.312×107 D、3.12×1073. 多项式x2+3x﹣2中,下列说法错误的是( )A、这是一个二次三项式 B、二次项系数是1 C、一次项系数是3 D、常数项是24. 数轴上的点A到原点的距离是4,则点A表示的数为 ( )A、4 B、-4 C、4或-4 D、2或-25. 如图,已知直线 , , ,则 等于( )
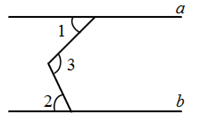 A、110° B、100° C、130° D、120°6. 如图,是一个正方体纸盒的平面展开图,则写有“为”字的面所对的面上的是( )
A、110° B、100° C、130° D、120°6. 如图,是一个正方体纸盒的平面展开图,则写有“为”字的面所对的面上的是( )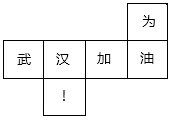 A、汉 B、! C、武 D、加7. 在防治新型冠状病毒的例行体温检查中,检查人员将高出37℃的部分记作正数,将低于37℃的部分记作负数,体温正好是37℃时记作“0”。记录一被测人员在一周内的体温测量结果分别为+0.1,-0.3,-0.5,+0.1,-0.6,+0.2, -0.4,那么,该被测者这一周中测量体温的平均值是( )A、37.1℃ B、37.31℃ C、36.8℃ D、36.69℃8. 若 和 的和是单项式,则代数式 的值是( )A、 B、 C、 D、9. 下面是小明做的一道多项式的加减运算题,但他不小心把一滴墨水滴在了上面. ,黑圆处即为被墨汁遮住的部分,那么被墨汁遮住的部分是( )A、 B、 C、 D、10. 如图,某广场地面的图案是用大小相同的黑、白正方形地砖镶嵌而成,图中第1个黑色L形由3个正方形组成,第2个黑色L形由7个正方形组成……那么第n个黑色L形的正方形个数是( )
A、汉 B、! C、武 D、加7. 在防治新型冠状病毒的例行体温检查中,检查人员将高出37℃的部分记作正数,将低于37℃的部分记作负数,体温正好是37℃时记作“0”。记录一被测人员在一周内的体温测量结果分别为+0.1,-0.3,-0.5,+0.1,-0.6,+0.2, -0.4,那么,该被测者这一周中测量体温的平均值是( )A、37.1℃ B、37.31℃ C、36.8℃ D、36.69℃8. 若 和 的和是单项式,则代数式 的值是( )A、 B、 C、 D、9. 下面是小明做的一道多项式的加减运算题,但他不小心把一滴墨水滴在了上面. ,黑圆处即为被墨汁遮住的部分,那么被墨汁遮住的部分是( )A、 B、 C、 D、10. 如图,某广场地面的图案是用大小相同的黑、白正方形地砖镶嵌而成,图中第1个黑色L形由3个正方形组成,第2个黑色L形由7个正方形组成……那么第n个黑色L形的正方形个数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 绝对值不大于4的所有整数的积等于.12. 若多项式2x2+3x+7的值为10,则多项式6x2+9x﹣7的值为 .13. 如图, ,若 ,则 的度数为.
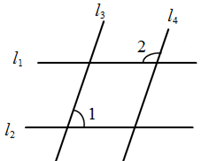 14. 一跳蚤在一直线上从O点开始,第1次向右跳1个单位,紧接着第2次向左跳2个单位,第3次向右跳3个单位,第4次向左跳4个单位,……,依此规律跳下去,当它跳第100次落下时,落点处离O点的距离是个单位.
14. 一跳蚤在一直线上从O点开始,第1次向右跳1个单位,紧接着第2次向左跳2个单位,第3次向右跳3个单位,第4次向左跳4个单位,……,依此规律跳下去,当它跳第100次落下时,落点处离O点的距离是个单位.三、解答题
-
15. 计算:(1)、(2)、(3)、(4)、16. 先化简,再求值: ,其 , .17. 如图, 于点D, 于点G,若 ,试说明: .下面是推理过程,请将推理过程补充完整.
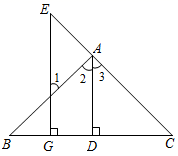
∵ 于点D, 于点G(已知),
∴ ()
∴ ()
∴ ()
∵ (已知),
∴ (等量代换)
又∵ (已证),
∴ ()
∴ (等量代换).
18. 如图,点C是线段 上一点,点M是线段 的中点,点N是线段 的中点. (1)、如果 , ,求 的长;(2)、如果 ,求 的长.19. 画图并度量,已知点A是直线l上一点,点M、N是直线l外两点,画图:
(1)、如果 , ,求 的长;(2)、如果 ,求 的长.19. 画图并度量,已知点A是直线l上一点,点M、N是直线l外两点,画图: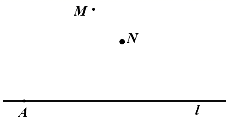 (1)、画线段 ,并用刻度尺找出它的中点B;(2)、画直线 ,交直线l于点C,并用量角器画出 的平分线 ;(3)、画出点M到直线l的垂线段 ,并度量点M到直线l的距离为 .(精确到 )20. 如图, ,直线 分别交 , 于E、F两点,且 平分 , ,求 的度数.
(1)、画线段 ,并用刻度尺找出它的中点B;(2)、画直线 ,交直线l于点C,并用量角器画出 的平分线 ;(3)、画出点M到直线l的垂线段 ,并度量点M到直线l的距离为 .(精确到 )20. 如图, ,直线 分别交 , 于E、F两点,且 平分 , ,求 的度数.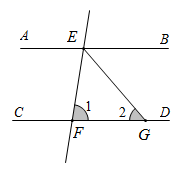 21. 疫情期间,为了满足市场上对口罩的需求,某厂家决定生产A、B两种款式的口罩.每天两种口罩的共生产量共500个,两种口罩的成本和售价如下表:
21. 疫情期间,为了满足市场上对口罩的需求,某厂家决定生产A、B两种款式的口罩.每天两种口罩的共生产量共500个,两种口罩的成本和售价如下表:成本(元/个)
售价(元/个)
A
5
8
B
7
9
若设每天生产A种口罩x个,
(1)、用含x的代数式表示该工厂每天的生产成本,并进行化简;(2)、用含x的代数式表示该工厂每天获得的利润,并将所列代数式进行化简;(3)、当 时,求每天获得的利润.(利润=售价-成本)22. 如图(1), 点 为直线 上一点,过点 作射线 , 将一直角的直角顶点放在点 处,即 反向延长射线 ,得到射线 .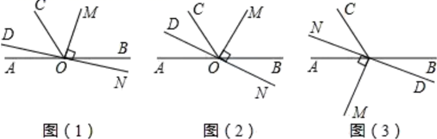 (1)、当 的位置如图(1)所示时,使 ,若 ,求 的度数.(2)、当 的位置如图(2)所示时,使一边 在 的内部,且恰好平分 ,
(1)、当 的位置如图(1)所示时,使 ,若 ,求 的度数.(2)、当 的位置如图(2)所示时,使一边 在 的内部,且恰好平分 ,问:射线 的反向延长线 是否平分 请说明理由:注意:不能用问题 中的条件
(3)、当 的位置如图 所示时,射线 在 的内部,若 .试探究 与 之间的数量关系,不需要证明,直接写出结论.