新疆维吾尔自治区乌鲁木齐市沙依巴克区2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-03-12 类型：期末考试

进入出卷网下载

一、单选题

1. 下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是（）

A、赵爽弦图 B、笛卡尔心形线 C、科克曲线 D、斐波那契螺旋线

查看试题解析
2. 下列说法正确的是（）．

A、投掷一枚质地均匀的硬币1000次，正面朝上的次数一定是500次 B、天气预报“明天降水概率10％，是指明天有10％的时间会下雨” C、一种福利彩票中奖率是千分之一，则买这种彩票1000张，一定会中奖 D、连续掷一枚均匀硬币，若5次都是正面朝上，则第六次仍然可能正面朝上

查看试题解析
3. 一元二次方程x²﹣x+2=0的根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、只有一个实数根

查看试题解析
4. 如图，已知C、D在以AB为直径的⊙O上，若∠CAB=30°，则∠D的度数是（）

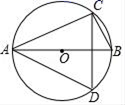A、30° B、70° C、75° D、60°

查看试题解析
5. 一元二次方程x²+6x﹣6=0配方后化为（）

A、（x﹣3）²=3 B、（x﹣3）²=15 C、（x+3）²=15 D、（x+3）²=3

查看试题解析
6. 如图，把 $△ A B C$ 绕点 $C$ 顺时针旋转35°得到 $△ A^{'} B^{'} C^{'}$ ， $A^{'}$ ， $B^{'}$ 交 $A C$ 于点 $D$ ，若 $A^{'} D = C D$ ，则 $∠ A$ 的度数为（）

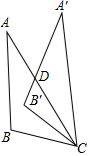A、25° B、35° C、45° D、55°

查看试题解析
7. 直线 $y = a x + b$ 与抛物线在 $y = a x^{2} + b x$ 同一平面直角坐标系中的图象大致为（）

A、 B、 C、 D、

查看试题解析
8. 如图，AB是⊙O的直径，弦CD⊥AB，垂足为点P，若CD＝AP＝8，则⊙O的直径为（）

A、10 B、8 C、5 D、3

查看试题解析
9. 制造一种产品，原来每件成本是100元，由于连续两次降低成本，现在的成本是81元，则平均每次降低的百分率是（）

A、8.5% B、9% C、9.5% D、10%

查看试题解析
10. 已知抛物线 $y = a x^{2} + b x + c$ 的顶点为 $D (- 1 ， 3)$ ，与x轴的一个交点在 $(- 3 ， 0)$ 和 $(- 2 ， 0)$ 之间，其部分图象如图，则以下结论：① $b^{2} - 4 a c > 0$ ；② $c - a = 3$ ；③ $a + b + c < 0$ ；④方程 $a x^{2} + b x + c = m$ （ $m \geq 2$ ）一定有实数根，其中正确的结论为（）

A、②③ B、①③ C、①②③ D、①②③④

查看试题解析

二、填空题

11. 已知点P（-b，2）与点Q（3，a）关于原点对称，则a+b的值是．

查看试题解析
12. 布袋中装有4个红球和3个黑球，它们除颜色外没有任何其他区别，小红从中随机摸出1个球，摸出红球的概率是．

查看试题解析
13. 关于 $x$ 的一元二次方程 $(a + 2) x^{2} - a x + a^{2} - 4 = 0$ 的一个根为0，则 $a =$ ．

查看试题解析
14. 已知圆锥的侧面积为8π $c m^{2}$ ，侧面展开图的圆心角为45°，该圆锥的母线长为cm.

查看试题解析
15. 如图所示，抛物线y=ax²+bx+c（a≠0）与x轴的两个交点分别为A（-1，0）和B（2，0），当y＜0时，x的取值范围是 .

查看试题解析
16. 如图，在△ABC．中，AB=BC，将△ABC绕点B顺时针旋转α度，得到△A₁BC₁ ， A₁B交AC于点E，A₁C₁分别交AC、BC于点D、F，下列结论：①∠CDF=α，②A₁E=CF，③DF=FC，④A₁F=CE．其中正确的是（写出正确结论的序号）．

查看试题解析

三、解答题

17. 解方程：2(x－3)＝3x(x－3)．

查看试题解析
18. 已知，在平面直角坐标系中， $△ A B C$ 的三个顶点坐标分别为 $A (- 1 ， - 1)$ ， $B (- 3 ， 3)$ ， $C (- 4 ， 1)$ .

①画出 $△ A B C$ 关于原点O的对称图形 $△ A_{1} B_{1} C_{1}$ ，并写出点A的对应点 $A_{1}$ 的坐标；

②画出 $△ A B C$ 绕点O按顺时针方向旋转90°后的图形 $△ A_{2} B_{2} C_{2}$ ，并写出点A的对应点 $A_{2}$ 的坐标.

查看试题解析
19. 一个不透明的口袋中装有4个分别标有数1，2，3，4的小球，它们的形状、大小完全相同，小红先从口袋里随机摸出一个小球记下数为x，小颖在剩下的3个球中随机摸出一个小球记下数为y，这样确定了点P(x，y)，请用“列表法”或“树状图法”求点P(x，y)在函数y=-x+5图象上的概率.

查看试题解析
20. 如图，AB为⊙O的直径，弦CD垂直平分OB于点E，点F在AB延长线上，∠AFC=30°.

(1)、求证：CF为⊙O的切线.

(2)、若半径ON⊥AD于点M，CE= $\sqrt{3}$ ，求图中阴影部分的面积.

查看试题解析
21. 如图，某校准备一面利用旧墙，其余三面用篱笆围成一个矩形花圃ABCD.墙可利用的最大长度为13米，一面利用旧墙，其余三面用篱笆围成，篱笆总长为24米.

(1)、若围成的花圃面积为 $70 m^{2}$ 时，求 $B C$ 的长；

(2)、如图，若计划在花圃中间用一道篱笆隔成两个小矩形，且花圃面积为 $78 m^{2}$ ，请你判断能否围成这样的花圃？如果能，求 $B C$ 的长；如果不能，请说明理由.

查看试题解析
22. 某百货商店服装在销售过程中发现，某品牌童装平均每天可售出20件，每件盈利40元，经市场调查发现，在进货不变的情况下，若每件童装每降价1元，日销售量将增加2件，当每件童装降价多少元时，这种童装一天的销售利润最多？最多利润是多少？

查看试题解析
23. 如图，已知抛物线 $y = a x^{2} + b x + 3$ 经过 $A (- 3 ， 0)$ ， $B (1 ， 0)$ 两点，其顶点为D，对称轴是直线l，l与x轴交于点H.

(1)、求该抛物线的解析式；

(2)、求 $△ D B C$ 的周长；

(3)、若点P是该抛物线对称轴l上的一个动点，求 $△ P B C$ 周长的最小值.

查看试题解析