陕西省榆林市清涧县2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-12 类型:期末考试
一、单选题
-
1. 已知 ,则 的值为( ).A、 B、 C、 D、2. 如图所示,该几何体的俯视图是( ).
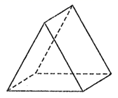 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列各组线段中,成比例的是( )A、2cm,3cm,4cm,5cm B、2cm,4cm,6cm,8cm C、3cm,6cm,8cm,12cm D、1cm,3cm,5cm,15cm4. 关于x的一元二次方程 的一个根为0,则实数a的值为A、 B、0 C、1 D、 或15. 若 与 都是反比例函数 图象上的点,则a的值是( )A、4 B、 C、2 D、6. 如图,直线a b c,AB= BC,若DF=9,则EF的长度为( )
3. 下列各组线段中,成比例的是( )A、2cm,3cm,4cm,5cm B、2cm,4cm,6cm,8cm C、3cm,6cm,8cm,12cm D、1cm,3cm,5cm,15cm4. 关于x的一元二次方程 的一个根为0,则实数a的值为A、 B、0 C、1 D、 或15. 若 与 都是反比例函数 图象上的点,则a的值是( )A、4 B、 C、2 D、6. 如图,直线a b c,AB= BC,若DF=9,则EF的长度为( ) A、9 B、5 C、4 D、37. 关于函数 ,下列说法中错误的是( ).A、函数的图象在第二、四象限 B、 的值随 值的增大而减小 C、函数的图象与坐标轴没有交点 D、函数的图象关于原点对称8. 如图,矩形 的对角线 , 相交于点 , ,若 的周长比 的周长大10,则 的长为( ).
A、9 B、5 C、4 D、37. 关于函数 ,下列说法中错误的是( ).A、函数的图象在第二、四象限 B、 的值随 值的增大而减小 C、函数的图象与坐标轴没有交点 D、函数的图象关于原点对称8. 如图,矩形 的对角线 , 相交于点 , ,若 的周长比 的周长大10,则 的长为( ).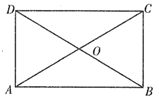 A、 B、 C、10 D、209. 如图,P为平行四边形ABCD边AD上一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S、S1、S2 , 若S=2,则S1+S2=( )
A、 B、 C、10 D、209. 如图,P为平行四边形ABCD边AD上一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S、S1、S2 , 若S=2,则S1+S2=( )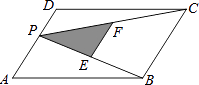 A、4 B、6 C、8 D、不能确定10. 如图,菱形ABCD的两条对角线长分别为AC=6,BD=8,点P是BC边上的一动点,则AP的最小值为( )
A、4 B、6 C、8 D、不能确定10. 如图,菱形ABCD的两条对角线长分别为AC=6,BD=8,点P是BC边上的一动点,则AP的最小值为( ) A、4 B、4.8 C、5 D、5.5
A、4 B、4.8 C、5 D、5.5二、填空题
-
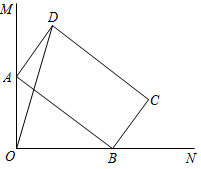
11. 如果两个相似三角形的相似比是2:3,那么它们的周长比是.12. 小明的身高为1.6米,他在阳光下的影长为0.8米,同一时刻,测得校园的旗杆的影长为4.5米,则该旗杆的高为米.13. 点A在反比例函数 的图象上, 轴于点B,点C在x轴负半轴上,且 .若 的面积为9,则k的值为.14. 如图, ,矩形 的顶点 , 分别在边 , 上,当点 在边 上移动时,点 随之在边 上移动, , ,运动过程中,点 到点 的最大距离为.
三、解答题
-
15. 解方程: .16. 如图,以原点O为位似中心,把△OAB放大后得到△OCD,求△OAB与△OCD的相似比.
 17. 如图,等腰 的顶角 ,请用尺规作图法,在 边上求作一点 ,使得 ∽ .(保留作图痕迹,不写作法)
17. 如图,等腰 的顶角 ,请用尺规作图法,在 边上求作一点 ,使得 ∽ .(保留作图痕迹,不写作法)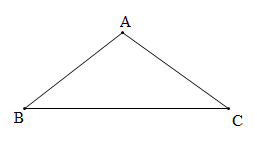 18. 某种商品标价500元/件,经过两次降价后售价为405元/件,并且两次降价的百分率相同.求这种商品每次降价的百分率.19. 已知函数 , ,当 时,函数 的最大值是 ,函数 的最小值是 ,求 和 的值.20. 如图,等边 的顶点 , 在矩形 的边 , 上,且 .
18. 某种商品标价500元/件,经过两次降价后售价为405元/件,并且两次降价的百分率相同.求这种商品每次降价的百分率.19. 已知函数 , ,当 时,函数 的最大值是 ,函数 的最小值是 ,求 和 的值.20. 如图,等边 的顶点 , 在矩形 的边 , 上,且 .求证:矩形 是正方形.
 21. 李叔叔驾驶小汽车从 地匀速行驶到 地,行驶里程为 ,设小汽车的行驶时间为 ,行驶速度为 ,且全程速度限定不超过 .(1)、求 与 之间的关系式;(2)、李叔叔上午8点驾驶小汽车从 地出发,需要在当天12点48分至14点(含12点48分和14点)间到达 地,求小汽车行驶速度 的范围.22. 小华和小雪玩摸牌游戏,现有同一副扑克牌中的2张“方块”,1张“梅花”和1张“红桃”,共4张扑克牌.游戏规则:先将这些扑克牌背面朝上洗匀后,放置在水平桌面上,再从中随机摸出一张牌,记下花色后放回,称为摸牌一次.(1)、小华随机摸牌20次,其中6次摸出的是“红桃”,求这20次中摸出“红桃”的频率;(2)、若小雪随机摸牌两次,请利用画树状图或列表的方法,求这两次摸出的牌都是“方块”的概率.23. 如图, 是某公园的一个圆形桌面的主视图, 是该桌面在一路灯下的影子, 是一个圆形凳面的主视图.(桌面、凳面均与地面平行)
21. 李叔叔驾驶小汽车从 地匀速行驶到 地,行驶里程为 ,设小汽车的行驶时间为 ,行驶速度为 ,且全程速度限定不超过 .(1)、求 与 之间的关系式;(2)、李叔叔上午8点驾驶小汽车从 地出发,需要在当天12点48分至14点(含12点48分和14点)间到达 地,求小汽车行驶速度 的范围.22. 小华和小雪玩摸牌游戏,现有同一副扑克牌中的2张“方块”,1张“梅花”和1张“红桃”,共4张扑克牌.游戏规则:先将这些扑克牌背面朝上洗匀后,放置在水平桌面上,再从中随机摸出一张牌,记下花色后放回,称为摸牌一次.(1)、小华随机摸牌20次,其中6次摸出的是“红桃”,求这20次中摸出“红桃”的频率;(2)、若小雪随机摸牌两次,请利用画树状图或列表的方法,求这两次摸出的牌都是“方块”的概率.23. 如图, 是某公园的一个圆形桌面的主视图, 是该桌面在一路灯下的影子, 是一个圆形凳面的主视图.(桌面、凳面均与地面平行)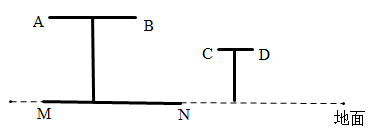 (1)、请标出路灯 的位置,并画出 在该路灯下的影子 ;(保留画图痕迹,光线用虚线表示)(2)、若桌面直径和桌面与地面的距离均为 ,并测得影子 ,求路灯 与地面的距离.24. 如图,一次函数 与反比例函数 的图象交于 , 两点.
(1)、请标出路灯 的位置,并画出 在该路灯下的影子 ;(保留画图痕迹,光线用虚线表示)(2)、若桌面直径和桌面与地面的距离均为 ,并测得影子 ,求路灯 与地面的距离.24. 如图,一次函数 与反比例函数 的图象交于 , 两点.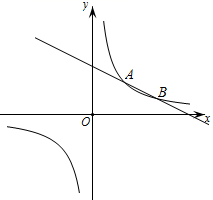 (1)、求这两个函数的表达式;(2)、在反比例函数 第三象限的图象上有一点 ,且点 到直线 的距离最短,求点 的坐标.25. 如图①,在 中, , 与 关于 对称.
(1)、求这两个函数的表达式;(2)、在反比例函数 第三象限的图象上有一点 ,且点 到直线 的距离最短,求点 的坐标.25. 如图①,在 中, , 与 关于 对称.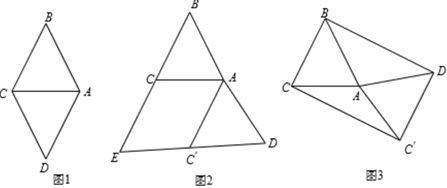 (1)、将图①中的 绕点 逆时针旋转角 ,使 ,得到如图②所示的 ,分别延长 和 交于点 ,则四边形 的形状是;(2)、将图①中的 绕点 逆时针旋转角 ,使 ,得到如图③所示的 ,连接 , ,得到四边形 ,判断四边形 的形状,并说明理由;(3)、如图③, , ,将 沿射线 的方向平移 ,得到 ,连接 , ,使四边形 恰好为正方形,求 值.
(1)、将图①中的 绕点 逆时针旋转角 ,使 ,得到如图②所示的 ,分别延长 和 交于点 ,则四边形 的形状是;(2)、将图①中的 绕点 逆时针旋转角 ,使 ,得到如图③所示的 ,连接 , ,得到四边形 ,判断四边形 的形状,并说明理由;(3)、如图③, , ,将 沿射线 的方向平移 ,得到 ,连接 , ,使四边形 恰好为正方形,求 值.