陕西省咸阳市武功县2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-12 类型:期末考试
一、单选题
-
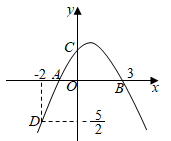
1. 已知方程 的一个根是 ,则 的值是( )A、 B、 C、 D、2. 下列几何体中,主视图和俯视图都为矩形的是( )A、
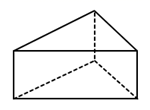 B、
B、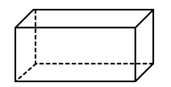 C、
C、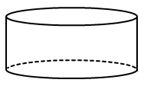 D、
D、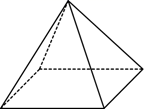 3. 若两个相似多边形的面积之比为1:4,则它们的周长之比为( )A、1:4 B、1:2 C、2:1 D、1:164. 在 中, ,则 的长是( )A、 B、 C、 D、5. 如图,在菱形ABOC中,AB=2,∠A=60°,菱形的一个顶点C在反比例函数y= (k≠0)的图象上,则反比例函数的解析式为( )
3. 若两个相似多边形的面积之比为1:4,则它们的周长之比为( )A、1:4 B、1:2 C、2:1 D、1:164. 在 中, ,则 的长是( )A、 B、 C、 D、5. 如图,在菱形ABOC中,AB=2,∠A=60°,菱形的一个顶点C在反比例函数y= (k≠0)的图象上,则反比例函数的解析式为( ) A、y= B、y= C、y= D、y=6. 如图,小球从A入口往下落,在每个交叉口都有向左或向右两种可能,且可能性相等,则小球从E出口落出的概率是( )
A、y= B、y= C、y= D、y=6. 如图,小球从A入口往下落,在每个交叉口都有向左或向右两种可能,且可能性相等,则小球从E出口落出的概率是( )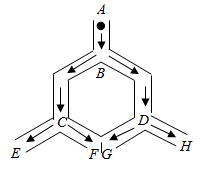 A、 B、 C、 D、7. 已知点 在反比例函数 的图象上,则下列结论正确的是( )A、 B、 C、 D、8. 如图,在正方形 中, 是 边上的动点, 于点 于点 ,则 的值为( )
A、 B、 C、 D、7. 已知点 在反比例函数 的图象上,则下列结论正确的是( )A、 B、 C、 D、8. 如图,在正方形 中, 是 边上的动点, 于点 于点 ,则 的值为( ) A、 B、 C、 D、9. 小明在学完《解直角三角形》一章后,利用测角仪和校园旗杆的拉绳测量校园旗杆的高度,如图,旗杆 的高度与拉绳 的长度相等,小明先将 拉到 的位置,测得 为水平线),测角仪 的高度为 米,则旗杆 的高度为( )
A、 B、 C、 D、9. 小明在学完《解直角三角形》一章后,利用测角仪和校园旗杆的拉绳测量校园旗杆的高度,如图,旗杆 的高度与拉绳 的长度相等,小明先将 拉到 的位置,测得 为水平线),测角仪 的高度为 米,则旗杆 的高度为( )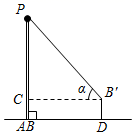 A、 米 B、 米 C、 米 D、 米10. 将抛物线 向左平移1个单位长度,得到抛物线 ,抛物线 与抛物线 关于x轴对称,则抛物线 的解析式为( )A、 B、 C、 D、
A、 米 B、 米 C、 米 D、 米10. 将抛物线 向左平移1个单位长度,得到抛物线 ,抛物线 与抛物线 关于x轴对称,则抛物线 的解析式为( )A、 B、 C、 D、二、填空题
-
11. 关于 的方程 是一元二次方程,则 的值为.12. 如图, 平分 且 ,则当 时, .
 13. 已知点 分别在反比例函数 的图象上,若点 与点 关于 轴对称,则 的值为.14. 如图,在矩形 中,AB=3,BC=4,点 分别是边 的中点,连接 ,得到一个新的四边形 则四边形 的面积为 .
13. 已知点 分别在反比例函数 的图象上,若点 与点 关于 轴对称,则 的值为.14. 如图,在矩形 中,AB=3,BC=4,点 分别是边 的中点,连接 ,得到一个新的四边形 则四边形 的面积为 .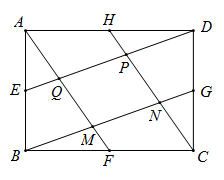
三、解答题
-
15. 解方程:4x2-8x+1=016. 已知α是锐角,且sin (α+15°)= ,计算 -4cosα-(π-3.14)0+tanα+ 的值.17. 如图.已知 各顶点的坐标分别为 .以点 为位似中心.将 放大为原来的 倍,得到 ,请在网格中画出 并写出点 的坐标.
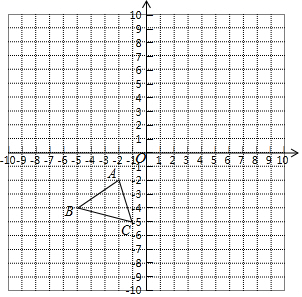 18. 如图,第二象限的角平分线 与反比例函数 的图象交于点A, 轴于点B, ,求 的值.
18. 如图,第二象限的角平分线 与反比例函数 的图象交于点A, 轴于点B, ,求 的值.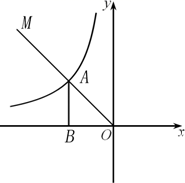 19. 如图,四边形 是平行四边形, ,且分别交对角线 于点 , ,连接 .若 ,求证:四边形 是菱形.
19. 如图,四边形 是平行四边形, ,且分别交对角线 于点 , ,连接 .若 ,求证:四边形 是菱形.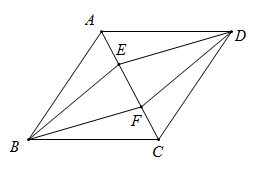 20. 王老师要装修自己带阁楼的新居(下图为新居剖面图),在建造客厅到阁楼的楼梯 时,为避免上楼时墙角 碰头,设计墙角 到楼梯的竖直距离 为 ,他量得客厅高 ,楼梯洞口宽 ,阁楼阳台宽 .请你帮助王老师解决问题:要使墙角 到楼梯的竖直距离 为 ,楼梯底端 到墙角 的距离 是多少米?
20. 王老师要装修自己带阁楼的新居(下图为新居剖面图),在建造客厅到阁楼的楼梯 时,为避免上楼时墙角 碰头,设计墙角 到楼梯的竖直距离 为 ,他量得客厅高 ,楼梯洞口宽 ,阁楼阳台宽 .请你帮助王老师解决问题:要使墙角 到楼梯的竖直距离 为 ,楼梯底端 到墙角 的距离 是多少米?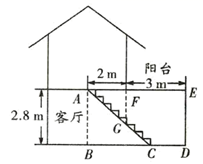 21. 某驻村扶贫小组实施产业扶贫,帮助贫困农户进行西瓜种植和销售.已知西瓜的成本为6元/千克,规定销售单价不低于成本,又不高于成本的两倍.经过市场调查发现,某天西瓜的销售量y(千克)与销售单价x(元/千克)的函数关系如下图所示:
21. 某驻村扶贫小组实施产业扶贫,帮助贫困农户进行西瓜种植和销售.已知西瓜的成本为6元/千克,规定销售单价不低于成本,又不高于成本的两倍.经过市场调查发现,某天西瓜的销售量y(千克)与销售单价x(元/千克)的函数关系如下图所示: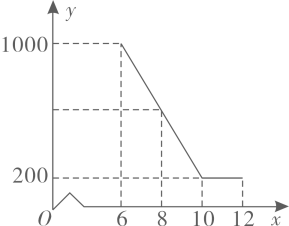 (1)、求y与x的函数解析式(也称关系式);(2)、求这一天销售西瓜获得的利润的最大值.22. “诵读经典,传承文明”,为了弘扬中华传统文化,某校近期举办了“国学经典诵读大赛”,诵读的篇目分成四种类型: .蒙学今诵; .爱国传承; .励志劝勉; .秀山丽水,每种类型的篇目数相同,参赛者需从这四种类型中随机抽取一种诵读类型.(1)、小颖参加了这次大赛,求她恰好抽中“ .爱国传承”的概率;(2)、小红和小明也参加了这次大赛,请用画树状图或列表法求他们抽中同一种类型篇目的概率.23. 如图,点O是线段AB上的一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB,CF⊥OF于点F.
(1)、求y与x的函数解析式(也称关系式);(2)、求这一天销售西瓜获得的利润的最大值.22. “诵读经典,传承文明”,为了弘扬中华传统文化,某校近期举办了“国学经典诵读大赛”,诵读的篇目分成四种类型: .蒙学今诵; .爱国传承; .励志劝勉; .秀山丽水,每种类型的篇目数相同,参赛者需从这四种类型中随机抽取一种诵读类型.(1)、小颖参加了这次大赛,求她恰好抽中“ .爱国传承”的概率;(2)、小红和小明也参加了这次大赛,请用画树状图或列表法求他们抽中同一种类型篇目的概率.23. 如图,点O是线段AB上的一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB,CF⊥OF于点F.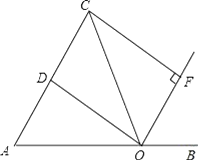 (1)、求证:四边形CDOF是矩形;(2)、当∠AOC多少度时,四边形CDOF是正方形?并说明理由.
(1)、求证:四边形CDOF是矩形;(2)、当∠AOC多少度时,四边形CDOF是正方形?并说明理由.