陕西省宝鸡市凤翔县2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-12 类型:期末考试
一、单选题
-
1. 如图所示的几何体的左视图是( )
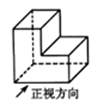
 A、A B、B C、C D、D2. 若x=1是方程ax2+bx+c=0的解,则( )A、a+b+c=1 B、a﹣b+c=0 C、a+b+c=0 D、a﹣b﹣c=03. 已知 ,则 ( )A、 B、 C、 D、4. 一个不透明的盒子里有n个除颜色外其它完全相同的小球,其中有6个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后在放回盒子,通过大量重复摸球实验后发现,摸到黄球的频率稳定在30%,那么可以推算出n大约是( )A、6 B、10 C、18 D、205. 如图,AB∥CD∥MN,点M,N分别在线段AD,BC上,AC与MN交于点E.则( )
A、A B、B C、C D、D2. 若x=1是方程ax2+bx+c=0的解,则( )A、a+b+c=1 B、a﹣b+c=0 C、a+b+c=0 D、a﹣b﹣c=03. 已知 ,则 ( )A、 B、 C、 D、4. 一个不透明的盒子里有n个除颜色外其它完全相同的小球,其中有6个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后在放回盒子,通过大量重复摸球实验后发现,摸到黄球的频率稳定在30%,那么可以推算出n大约是( )A、6 B、10 C、18 D、205. 如图,AB∥CD∥MN,点M,N分别在线段AD,BC上,AC与MN交于点E.则( )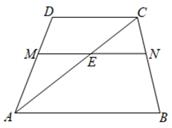 A、 B、 C、 D、6. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC= ,BC=2,则sin∠ACD的值为( )
A、 B、 C、 D、6. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC= ,BC=2,则sin∠ACD的值为( )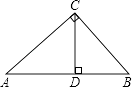 A、 B、 C、 D、7. 某数学兴趣小组利用阳光下的影子测量建筑物的高度,已知小明的身高1.5m,测量其影子为1.2m,建筑物的影长为14m,则建筑物的高是( )m.A、16.5 B、17 C、17.5 D、188. 如图, 与 位似,其位似中心为点 ,且 为 的中点,则 与 的面积比是( )
A、 B、 C、 D、7. 某数学兴趣小组利用阳光下的影子测量建筑物的高度,已知小明的身高1.5m,测量其影子为1.2m,建筑物的影长为14m,则建筑物的高是( )m.A、16.5 B、17 C、17.5 D、188. 如图, 与 位似,其位似中心为点 ,且 为 的中点,则 与 的面积比是( )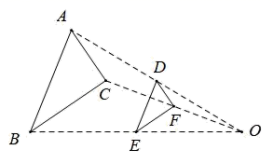 A、 B、 C、 D、9. 已知点 都在反比例函数 的图象上,那么 与 的大小关系是( )A、 B、 C、 D、10. 如图,点 是 中斜边 (不与 , 重合)上一动点,分别作 于点 ,作 于点 ,连接 、 ,若 , ,当点 在斜边 上运动时,则 的最小值是( )
A、 B、 C、 D、9. 已知点 都在反比例函数 的图象上,那么 与 的大小关系是( )A、 B、 C、 D、10. 如图,点 是 中斜边 (不与 , 重合)上一动点,分别作 于点 ,作 于点 ,连接 、 ,若 , ,当点 在斜边 上运动时,则 的最小值是( ) A、1.5 B、2 C、4.8 D、2.4
A、1.5 B、2 C、4.8 D、2.4二、填空题
-
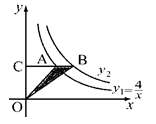
11. 已知线段AB的长为2厘米,点P是线段AB的黄金分割点(AP<BP),那么BP的长是 厘米.12. 把抛物线y= x2向左平移3个单位,再向下平移2个单位后,所得的抛物线的表达式是13. 双曲线 、 在第一象限的图象如图, ,过 上的任意一点 ,作 轴的平行线交 于 ,交 轴于 ,若 ,则 的解析式是.
 14. 如图,四边形 是一张长方形纸片,将该纸片对折,使顶点 与顶点 重合, 为折痕,若 、 ,则图中阴影部分的面积为.
14. 如图,四边形 是一张长方形纸片,将该纸片对折,使顶点 与顶点 重合, 为折痕,若 、 ,则图中阴影部分的面积为.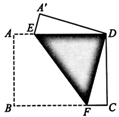
三、解答题
-
15. 如图, 中, ,尺规作图:在 上求作 点,使得 与 相似;(保留作图痕迹,不写作法)
 16. 计算: .17. 如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
16. 计算: .17. 如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点. (1)、求证:△MBA≌△NDC;(2)、四边形MPNQ是什么样的特殊四边形?请说明理由.18. 如图,小丽在观察某建筑物 ,请你根据小亮在阳光下的投影,画出建筑物 在阳光下的投影.
(1)、求证:△MBA≌△NDC;(2)、四边形MPNQ是什么样的特殊四边形?请说明理由.18. 如图,小丽在观察某建筑物 ,请你根据小亮在阳光下的投影,画出建筑物 在阳光下的投影.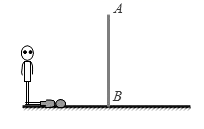 19. 在国家的宏观调控下,某市的商品房成交价由今年3月份的5000元/m2下降到5月份的4050元/m2 .(1)、问4、5两月平均每月降价的百分率是多少;(2)、如果房价继续回落,按此降价的百分率,你预测到7月分该市的商品房成交均价是否会跌破3000元/m2 . 请说明理由.20. 如图,等边 中,点 、 分别在边 、 上, .
19. 在国家的宏观调控下,某市的商品房成交价由今年3月份的5000元/m2下降到5月份的4050元/m2 .(1)、问4、5两月平均每月降价的百分率是多少;(2)、如果房价继续回落,按此降价的百分率,你预测到7月分该市的商品房成交均价是否会跌破3000元/m2 . 请说明理由.20. 如图,等边 中,点 、 分别在边 、 上, .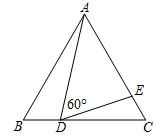 (1)、求证: ∽ ;(2)、若 , ,求等边 的边长.21. 大雁塔是现存最早规模最大的唐代四方楼阁式砖塔,被国务院批准列入第一批全国重点文物保护单位,某校社会实践小组为了测量大雁塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆 ,这时地面上的点E,标杆的顶端点D,大雁塔的塔尖点B正好在同一直线上,测得 米,将标杆向后平移到点G处,这时地面上的点F,标杆的顶端点H,大雁塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与大雁塔底处的点A在同一直线上),这时测得 米, 米,请你根据以上数据,计算大雁塔的高度 .
(1)、求证: ∽ ;(2)、若 , ,求等边 的边长.21. 大雁塔是现存最早规模最大的唐代四方楼阁式砖塔,被国务院批准列入第一批全国重点文物保护单位,某校社会实践小组为了测量大雁塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆 ,这时地面上的点E,标杆的顶端点D,大雁塔的塔尖点B正好在同一直线上,测得 米,将标杆向后平移到点G处,这时地面上的点F,标杆的顶端点H,大雁塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与大雁塔底处的点A在同一直线上),这时测得 米, 米,请你根据以上数据,计算大雁塔的高度 .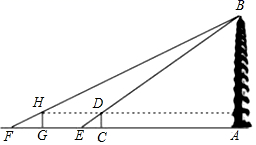 22. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内, 的三个顶点坐标分别为 , , .
22. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内, 的三个顶点坐标分别为 , , .
(1)画出 关于 轴对称的 ;
(2)画出 以点 为位似中心的位似图形 , 与 的位似比为 (画一个即可).23. 2019年10月20日上午7:30西安国际马拉松赛鸣枪开跑.本届赛事设有马拉松、半程马拉松、欢乐跑三个项目,小智和小慧参加了该赛事的志愿者服务工作,组委会将志愿者随机分配到三个项目组中的一个.(1)、小智被分配到欢乐跑项目组的概率为.(2)、用树状图或列表法求小智和小慧被分到同一个项目组的概率.24. 如图,一次函数 ( , 为常数, )的图象与反比例函数 ( )的图象交于点 与点 ; (1)、求一次函数与反比例函数的解析式;(2)、根据图象直接写出当 为何值时, ;(3)、求出 的面积.25. 如图,已知A,B两点的坐标分别为 , ,点P,Q同时出发分别作匀速运动,其中点P从点A出发沿AO向终点O运动,速度为每秒3个单位长度,点Q从点O出发沿OB运动,速度为每秒2个单位长度,当这两个点有一点到达自己的终点时,另一点也停止运动,设P,Q运动时间为t秒.
(1)、求一次函数与反比例函数的解析式;(2)、根据图象直接写出当 为何值时, ;(3)、求出 的面积.25. 如图,已知A,B两点的坐标分别为 , ,点P,Q同时出发分别作匀速运动,其中点P从点A出发沿AO向终点O运动,速度为每秒3个单位长度,点Q从点O出发沿OB运动,速度为每秒2个单位长度,当这两个点有一点到达自己的终点时,另一点也停止运动,设P,Q运动时间为t秒.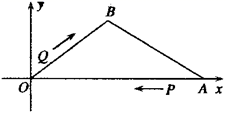 (1)、求t的取值范围;(2)、若以O,P,Q为顶点的三角形与 相似,求此时t的值;(3)、是否存在t,使得 为等腰三角形?若存在,请直接写出运动时间t;若不存在,请说明理由.
(1)、求t的取值范围;(2)、若以O,P,Q为顶点的三角形与 相似,求此时t的值;(3)、是否存在t,使得 为等腰三角形?若存在,请直接写出运动时间t;若不存在,请说明理由.