河南省洛阳市汝阳县2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-03-12 类型：期末考试

进入出卷网下载

一、单选题

1. 下列式子一定是二次根式的是（）

A、 $\sqrt{- x - 2}$ B、 $\sqrt{x}$ C、 $\sqrt{x^{2} + 2}$ D、 $\sqrt{x^{2} - 2}$

查看试题解析
2. 下列说法错误的是（）

A、必然事件的概率为1 B、数据1、2、2、3的平均数是2 C、数据5、2、﹣3、0的极差是8 D、如果某种游戏活动的中奖率为40%，那么参加这种活动10次必有4次中奖

查看试题解析
3. 抛物线 $y = 2 {(x + 1)}^{2} - \frac{1}{2}$ 的顶点坐标为（）

A、 $(1, - \frac{1}{2})$ B、 $(- 1, - \frac{1}{2})$ C、 $(- 1, \frac{1}{2})$ D、 $(1, \frac{1}{2})$

查看试题解析
4. 如图，直线 $l_{1} ∥ l_{2} ∥ l_{3}$ ，直线 $A C$ 分别交 $l_{1}$ ， $l_{2}$ ， $l_{3}$ 于点 $A$ ， $B$ ， $C$ ；直线 $D F$ 分别交 $l_{1}$ ， $l_{2}$ ， $l_{3}$ 于点 $D$ ， $E$ ， $F$ ， $A C$ 与 $D F$ 相交于点 $H$ ，且 $A H = 2$ ， $H B = 1$ ， $B C = 5$ ，则 $\frac{D E}{E F}$ 的值为（）

A、 $\frac{1}{2}$ B、 $2$ C、 $\frac{3}{5}$ D、 $\frac{2}{5}$

查看试题解析
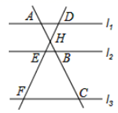5. 如图，要测量B点到河岸AD的距离，在A点测得∠BAD＝30°，在C点测得∠BCD＝60°，又测得AC＝100米，则B点到河岸AD的距离为（）

A、100米 B、50 $\sqrt{3}$ 米 C、 $\frac{200 \sqrt{3}}{3}$ 米 D、50米

查看试题解析
6. 已知点 $A (1, y_{1})$ 、 $B (- \sqrt{2}, y_{2})$ 、 $C (- 2, y_{3})$ 在函数 $y = 2 {(x + 1)}^{2} - \frac{1}{2}$ 上.则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小关系是（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{1} > y_{3} > y_{2}$ C、 $y_{3} > y_{1} > y_{2}$ D、 $y_{2} > y_{1} > y_{3}$

查看试题解析
7. 方程 $(m - 2) x^{2} - \sqrt{3 - m} x + \frac{1}{4} = 0$ 有两个实数根，则m的取值范围（）

A、 $m > \frac{5}{2}$ B、 $m \leq \frac{5}{2}$ 且 $m \neq 2$ C、 $m \geq 3$ D、 $m \leq 3$ 且 $m \neq 2$

查看试题解析
8. 你知道吗？股票每天的涨、跌幅均不超过10%，即当涨了原价的10%后，便不能再涨，叫做涨停；当跌了原价的10%后，便不能再跌，叫做跌停．已知一支股票某天跌停，之后两天时间又涨回到原价，若这两天此股票股价的平均增长率为x，则x满足的方程是（）

A、（1+x）²= $\frac{11}{10}$ B、x+2x= $\frac{11}{10}$ C、（1+x）²= $\frac{10}{9}$ D、1+2x= $\frac{10}{9}$

查看试题解析
9. 如图，在下列网格中，小正方形的边长均为1，点A、B、O都在格点上，则 $∠ A O B$ 的正弦值是（）

A、 $\frac{3 \sqrt{10}}{10}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{10}}{10}$ D、 $\frac{1}{10}$

查看试题解析
10. 如图，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C = 2$ ，AB的中点为D.以C为原点，射线CB为x轴的正方向，射线CA为y轴的正方向建立平面直角坐标系.P是BC上的一个动点，连接AP、DP，则 $A P + D P$ 最小时，点P的坐标为（）.

A、 $(\frac{2}{3} ， 0)$ B、 $(\frac{\sqrt{2}}{2} ， 0)$ C、 $(\frac{\sqrt{10}}{10} ， 0)$ D、 $(\frac{1}{10} ， 0)$

查看试题解析

二、填空题

11. 方程 $x^{2} - 4 x = 0$ 的解为.

查看试题解析
12. 若方程 $x^{2} + 8 x - 4 = 0$ 的两根为 $x_{1}$ 、 $x_{2}$ ，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}} =$ .

查看试题解析
13. 在平面直角坐标系内抛物线 $y = x^{2} - 2 x + 3$ 的图象先向左平移3个单位，再向上平移5个单位后图象对应的二次函数解析式为.

查看试题解析
14. 如图，在 $Δ A B C$ 中， $D$ 、 $E$ 分别是 $A B$ 、 $B C$ 上的点，且 $D E ∥ A C$ ，若 $S_{Δ B D E} ： S_{Δ C D E} = 1 ： 4$ ，则 $S_{Δ B D E} ： S_{Δ A C D} =$ .

查看试题解析
15. 如图是二次函数 $y = a x^{2} + b x + c$ 的图象的一部分且图象过点 $A (- 3 ， 0)$ ，对称轴为 $x = - 1$ ，给出四个结论：① $b^{2} > 4 a c$ ；②图像可能过 $(2 ， 0)$ ；③ $a + b + c = 0$ ；④ $a > b$ .其中正确的是（填序号）

查看试题解析

三、解答题

16. 已知： $x = 1 - 2 \cos 45 °$ ， $y = 1 + 2 \sin 45 °$ ，求 $x^{2} + y^{2} - x y - 2 x + 2 y$ 的值.

查看试题解析
17. 吸烟有害健康!据了解，我国已经从2011年元月1日起在公共场所实行“禁烟”，为配合“禁烟”行动，某校组织同学们在某社区开展了“你支持哪种戒烟方式”的问卷调查，征求市民的意见，并将调查结果整理后制成了如下统计图：

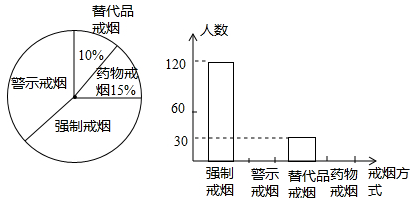
根据统计图解答：

(1)、同学们一共随机调查了多少人？

(2)、请你把两个统计图补充完整（扇形统计图中也需要填）；

(3)、如果在该社区随机咨询一位市民，那么该市民支持“强制戒烟”的概率是多少？假定该社区有1万人，请估计该地区大约有多少人支持“警示戒烟”这种方式.

查看试题解析
18. 在3×3的方格纸中，点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.

(1)、从A、D、E、F四点中任意取一点，以所取的这一点及B、C为顶点三角形，则所画三角形是等腰三角形的概率是；

(2)、从A、D、E、F四点中先后任意取两个不同的点，以所取的这两点及B、C为顶点画四边形，求所画四边形是平行四边形的概率（用树状图或列表求解）.

查看试题解析
19. 汝阳某公司举办热气球表演来庆祝开业，如图，小敏、小亮从A，B两地观测空中C处一个气球，分别测得仰角为 $37 °$ 和 $45 °$ ，A、B两地相距100 m.当气球沿与BA平行地飘移100秒后到达D处时，在A处测得气球的仰角为 $60 °$ .

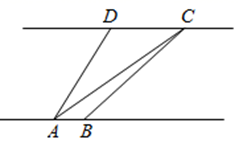(1)、求气球的高度；

(2)、求气球飘移的平均速度.（参考数据： $\sin 37 ° = 0.6$ ， $\cos 37 ° = 0.8$ ， $\tan 37 ° = 0.75$ ， $\sqrt{3} \approx 1.7$ .）

查看试题解析
20. 把一边长为40cm 的正方形硬纸板，进行适当的剪裁，折成一个长方体形盒子（纸板的厚度忽略不计）.如图若在正方形硬纸板的四角各剪一个同样大小的正方形，将剩余部分折成一个无盖的长方体形盒子.

(1)、要使折成的长方体形盒子的底面积为 $484 {cm}^{2}$ ，那么剪掉的正方形的边长为多少？

(2)、折成的长方体形盒子的侧面积是否有最大值？如果有，求出这个最大值和此时剪掉的正方形的边长；如果没有，说明理由.

查看试题解析
21. 如图，抛物线y＝﹣x²+5x+n经过点A(1，0)，与y轴交于点B．

(1)、求抛物线的解析式；

(2)、P是y轴正半轴上一点，且△PAB是以AB为腰的等腰三角形，试求P点坐标．

查看试题解析
22. 如图，Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm，动点P从点B出发，在BA边上以每秒5cm的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒4cm的速度向点B匀速运动，运动时间为t秒（0＜t＜2），连接PQ．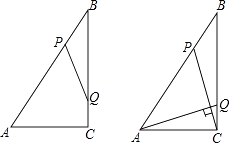

(1)、若△BPQ与△ABC相似，求t的值；

(2)、连接AQ，CP，若AQ⊥CP，求t的值．

查看试题解析
23. 如图，已知抛物线 $y = a x^{2} + b x + 3 (a \neq 0)$ 与x轴交于点 $A (1 ， 0)$ 和点 $B (- 3 ， 0)$ ，与y轴交于点C.（平面直角坐标系内两点间距离公式：点 $(x_{1} ， y_{1})$ 与点 $(x_{2} ， y_{2})$ 的距离为 $\sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2}}$ .）

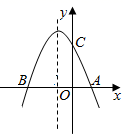(1)、求抛物线的解析式；

(2)、若 $- 2 \leq x \leq 0$ 时，画出函数图象，并根据图像直接写出函数的最大值与最小值；

(3)、若点E为第二象限抛物线上一动点，连接BE、CE，求当四边形BOCE面积取最大值时，求E点的坐标.

查看试题解析